LP Examples Solid Waste Management A SOLID WASTE

A SOLID WASTE PROBLEM A city generates 200 tons/day of solid wastes and must

MODEL FORMULATION MIN 7 X 1 + 8 X 2 + 6 X 3

SOLID WASTE SOLUTION using LINDO Objective function Value = $1380 X 1 = 120;

SOIL STABILITY PROBLEM In order to assure adequate stability under load repetition, a soil

MODEL FORMULATION MIN 0. 35 XA + 0. 65 XB SUBJECT TO L. L.

Case 2: LINDO OUTPUT SOLUTION: LP OPTIMUM FOUND AT STEP 4 OBJECTIVE FUNCTION VALUE

Slides: 8

Download presentation

LP Examples Solid Waste Management

A SOLID WASTE PROBLEM A city generates 200 tons/day of solid wastes and must dispose it to three landfills. The data about the cost is given in the table. For environmental reason all the three landfills has to be utilized. Develop the needed equations (objective function and constraints) for Linear programming model to find the optimal distribution of the waste to the three landfills. Landfill Maximum capacity (tons/day) L 1 L 2 L 3 120 100 50 Cost of transfer to landfill ($/ton) 4 3 2 Cost of disposal at the landfill ($/ton) 3 5 4

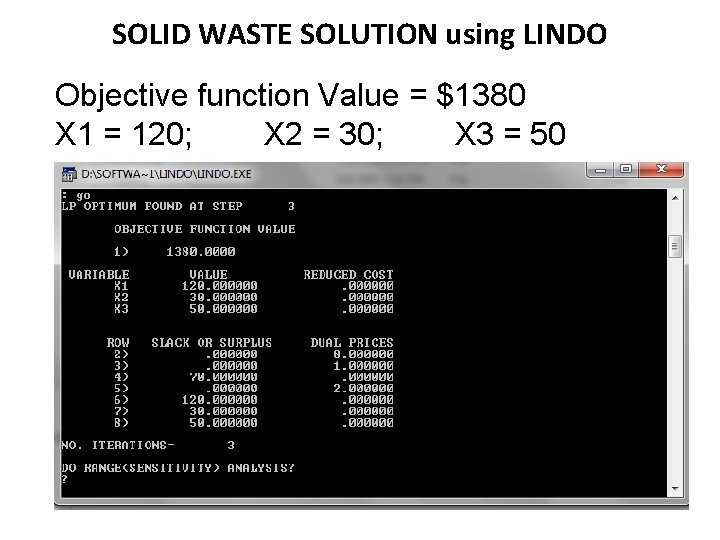
MODEL FORMULATION MIN 7 X 1 + 8 X 2 + 6 X 3 SUBJECT TO X 1 + X 2 + X 3 = 200 X 1 <= 120 X 2 <= 100 X 3 <= 50 X 1 >= 0 X 2 >= 0 X 3 >= 0 END

SOLID WASTE SOLUTION using LINDO Objective function Value = $1380 X 1 = 120; X 2 = 30; X 3 = 50

LP Example of Soil Stability

SOIL STABILITY PROBLEM In order to assure adequate stability under load repetition, a soil mixture for base and sub-base courses in the construction of a certain highway must have a liquid limit, 21=<LL<=28, and a Plasticity Index, 4=<PI<=6. Two materials, A and B, are available as follows: Properties LL PI Cost ($/cu. m ) A 35 8 $. 35 B 20 3. 5 $. 65 Assume that the LL and the PI are linear functions of the combinations of the two materials A and B and determine the optimal proportion of base and sub-base.

MODEL FORMULATION MIN 0. 35 XA + 0. 65 XB SUBJECT TO L. L. 35 XA + 20 XB >= 21 L. L. 35 XA + 20 XB <= 28 P. I. 8 XA + 3. 5 XB >= 4 P. I. 8 XA + 3. 5 XB <= 6 Proportionality XA + XB = 1 END

Case 2: LINDO OUTPUT SOLUTION: LP OPTIMUM FOUND AT STEP 4 OBJECTIVE FUNCTION VALUE 1). 4900000 VARIABLE VALUE REDUCED COST XA. 533333. 000000 XB. 466667. 000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 7. 000000 3). 000000. 020000 4) 1. 9000000 5). 1000000 6). 000000 -1. 050000 NO. ITERATIONS= 4 RANGE(SENSITIVITY) ANALYSIS: Y? : RANGES IN WHICH THE BASIS IS UNCHANGED OBJ COEFFICIENT RANGES VARIABLE CURRENT ALLOWABLE COEF INCREASE XA. 350000. 300000 XB. 650000 INFINITY RIGHTHAND SIDE RANGES ROW CURRENT ALLOWABLE RHS INCREASE 2 21. 000000 7. 000000 3 28. 000000. 333333 4 4. 000000 1. 900000 5 6. 000000 INFINITY 6 1. 000000. 400000 ALOWABLE INFINITY. 300000 ALOWABLE INFINITY 6. 333333 INFINITY. 100000. 040000 DECREASE 8