Low temperature specific heat of solids James C

Low temperature specific heat of solids James C. Ho

For some 200 articles on low temperature specific heat and superconductivity, I have many coauthors including: Members of the U. S. National Academy of Sciences Ching-Wu Chu, Theodore Geballe, John Hulm, Bernd Matthias, Maw-Kuen Wu Members of the U. S. National Academy of Engineering Karl Gschneidner, John Hulm, Robert Jaffee Fellow of British Royal Society Sir John Enderby Members of the Academia Sinica (Taiwan) Ching-Wu Chu, Maw-Kuen Wu Member of Chinese Academy of Science Weiyan Guan

Low temperatures Specific heat and entropy in chemical thermodynamics Low temperature specific heat in solid state physics Phonon (lattice) Conduction electrons Nuclear magnetic moments Critical phenomena Superconductivity Magnetic transitions Some applications to materials science Magnetic clusters Electron localization Non-uniform superconductors Nano-size effect

Low temperatures How low is low? How low can we go? How low do we need to go?

17 th-century depiction of Leiden University Library

Walther Nernst (Nobel prize in Chemistry, 1920) developed in 1906 -1912 the 3 rd law of thermodynamics (zero entropy at zero degree)

Specific heat and entropy in chemical thermodynamics Entropy change determination relies on specific heat measurements: ΔS = δQ/T = ∫(C/T) d. T _______________________ U = Q – W d. U = δQ – Pd. V (∂U/∂T)V = (∂Q/∂T)V ≡ CV H = U + PV d. U = δQ +Vd. P (∂H/∂T)p = (∂Q/∂T)p ≡ Cp Cp – CV = VT(α 2/βT) α: Coefficient of linear thermal expansion βT: Isothermal compressibility

Early models of specific heat of solids The Dulong-Petit law (1819): CV = 3 Nk (harmonic oscillators) ____________ The Einstein model (1907) (quantized harmonic oscillators) When Nernst learned of Einstein's paper, he was so excited that he traveled all the way from Berlin to Zurich to meet with Einstein.

Heike Kamerlingh Onnes (Leiden University, 1853 -1926) first liquefied helium in 1908 and discovered superconductivity in 1911. 1913 Nobel Prize in Physics

Einstein and Kamerlingh Onnes

Specific heat and entropy in chemical thermodynamics Low temperature specific heat in solid state physics Phonon (lattice) Conduction electrons Nuclear magnetic moments Critical phenomena Superconductivity Magnetic transitions Some applications to materials science Magnetic clusters Electron localization Non-uniform superconductors Nano-size effect

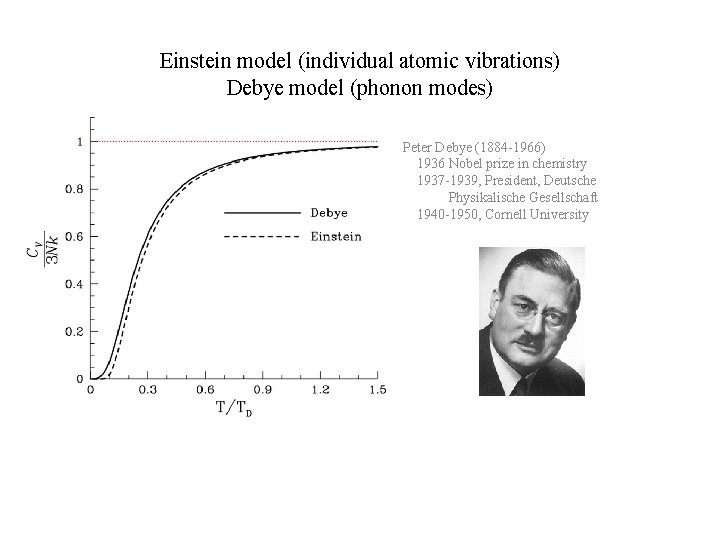
Einstein model (individual atomic vibrations) Debye model (phonon modes) Peter Debye (1884 -1966) 1936 Nobel prize in chemistry 1937 -1939, President, Deutsche Physikalische Gesellschaft 1940 -1950, Cornell University

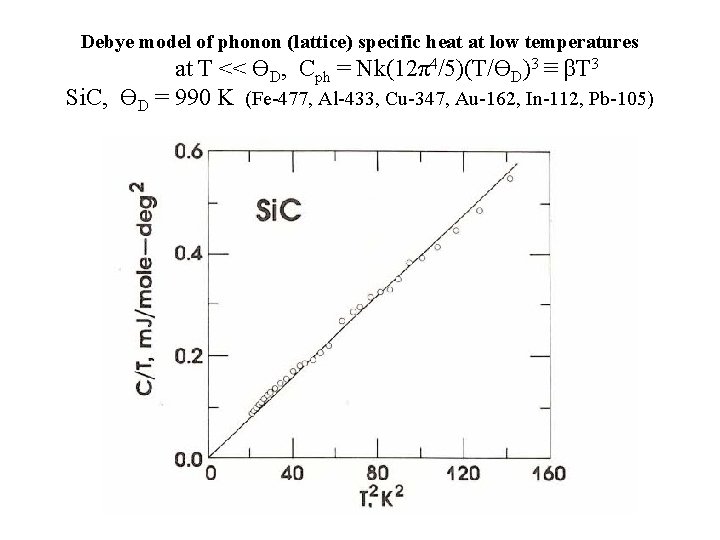
Debye model of phonon (lattice) specific heat at low temperatures at T << ϴD, Cph = Nk(12π4/5)(T/ϴD)3 ≡ βT 3 Si. C, ϴD = 990 K (Fe-477, Al-433, Cu-347, Au-162, In-112, Pb-105)

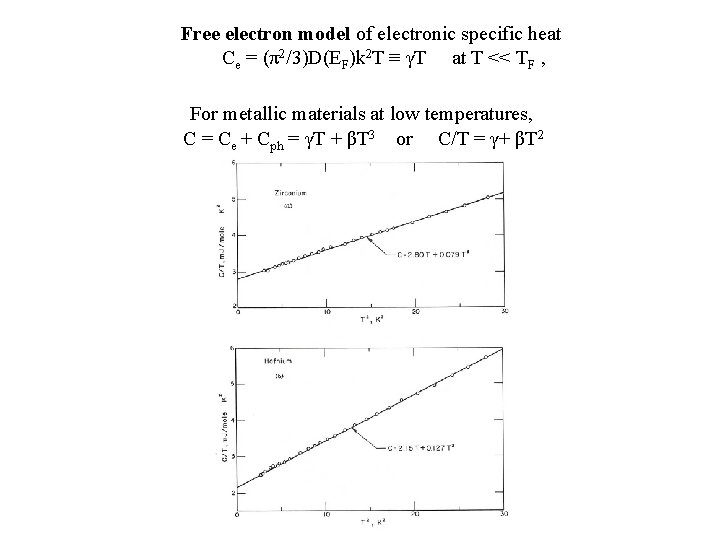
Free electron model of electronic specific heat Ce = (π2/3)D(EF)k 2 T ≡ γT at T << TF , For metallic materials at low temperatures, C = Ce + Cph = γT + βT 3 or C/T = γ+ βT 2

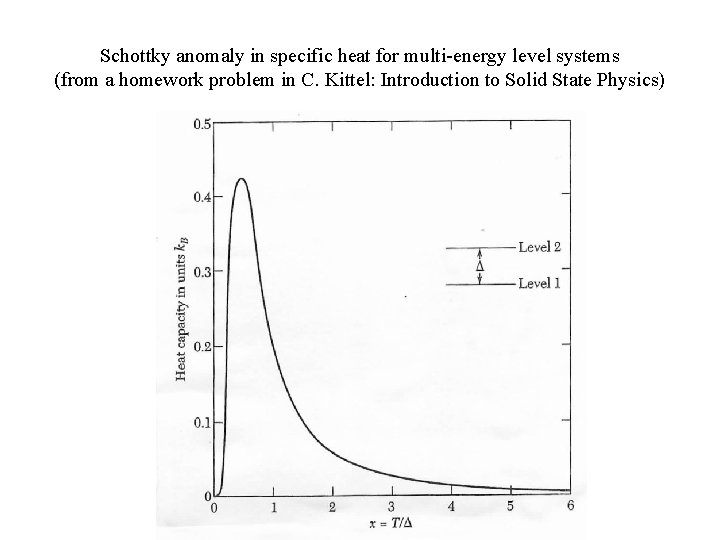
Schottky anomaly in specific heat for multi-energy level systems (from a homework problem in C. Kittel: Introduction to Solid State Physics)

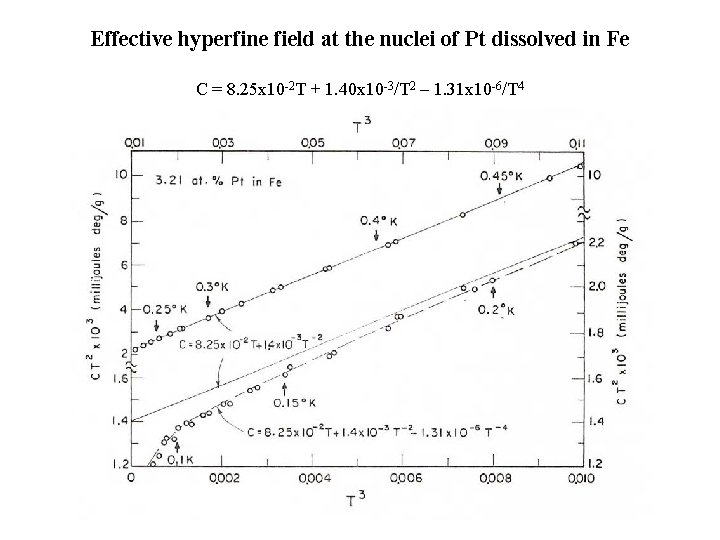
Nuclear specific heat. In magnetically ordered materials, interactions between s-electrons (non-zero density at nucleus) and the nuclear moment μ behave as an extremely large effective field He. It causes nuclear energy splitting, and in turn yields a Schottky-type specific heat. At temperatures T ˃˃ μHe/k (often near or less than 1 K), CN = Nk[(I+1)/3 I](μHe/k. T)2 – [(I+1)(2 I 2+2 I+1)/30 I 3](μHe/k. T)4 + …. = A/T 2 – A’/T 4 + ….

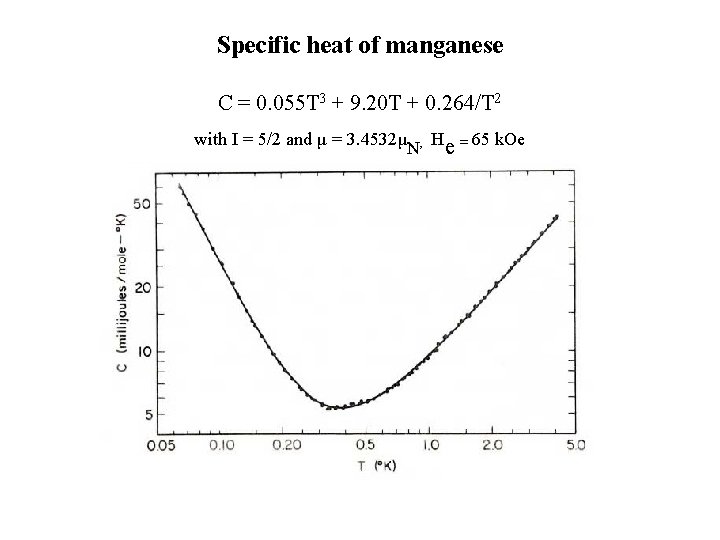
Specific heat of manganese C = 0. 055 T 3 + 9. 20 T + 0. 264/T 2 with I = 5/2 and μ = 3. 4532μN, He = 65 k. Oe

Effective hyperfine field at the nuclei of Pt dissolved in Fe C = 8. 25 x 10 -2 T + 1. 40 x 10 -3/T 2 – 1. 31 x 10 -6/T 4

Specific heat and entropy in chemical thermodynamics Low temperature specific heat in solid state physics Phonon (lattice) Conduction electrons Nuclear magnetic moments Critical phenomena Superconductivity Magnetic transitions Some applications to materials science Magnetic clusters Electron localization Non-uniform superconductors Nano-size effect

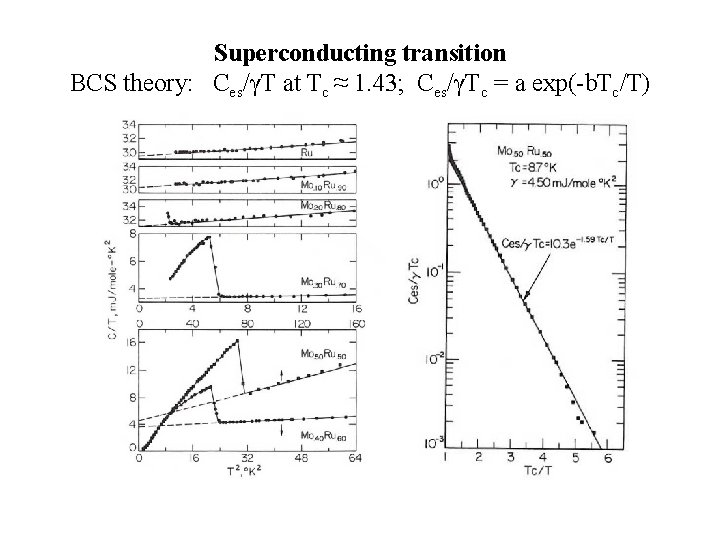
Superconducting transition BCS theory: Ces/γT at Tc ≈ 1. 43; Ces/γTc = a exp(-b. Tc/T)

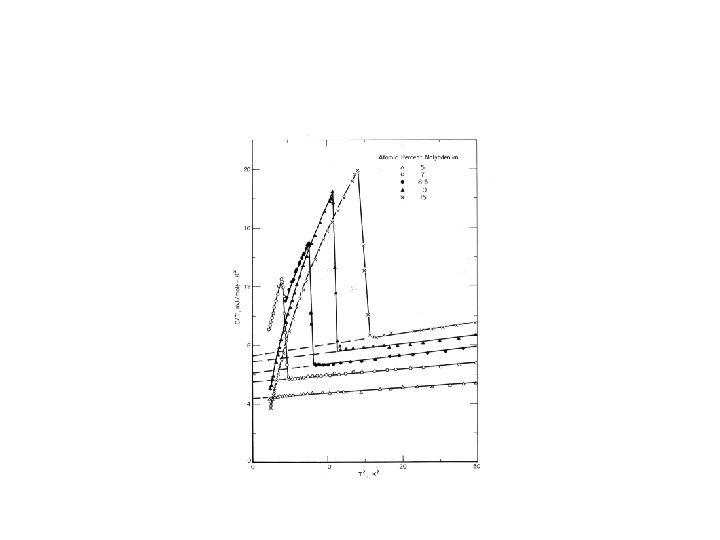
BCS theory: Tc ≈ ϴD exp[-1/D(EF)V] V: electron-phonon interaction parameter Superconducting transitions in Ti-Mo alloys (V = constant? )

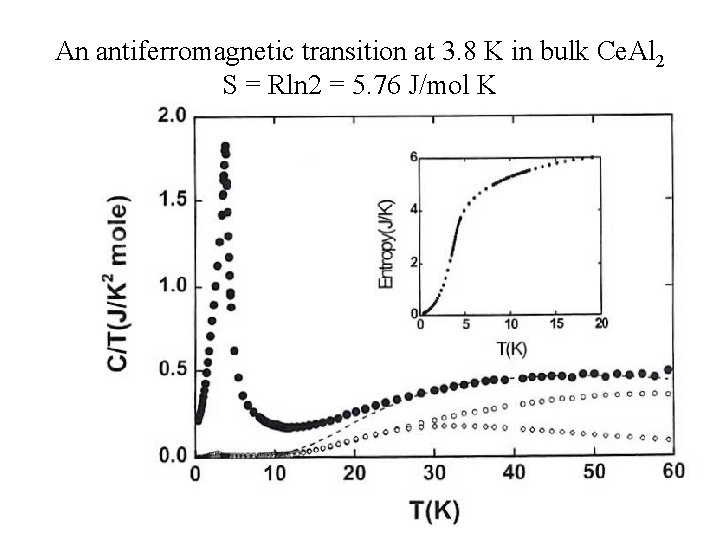
An antiferromagnetic transition at 3. 8 K in bulk Ce. Al 2 S = Rln 2 = 5. 76 J/mol K

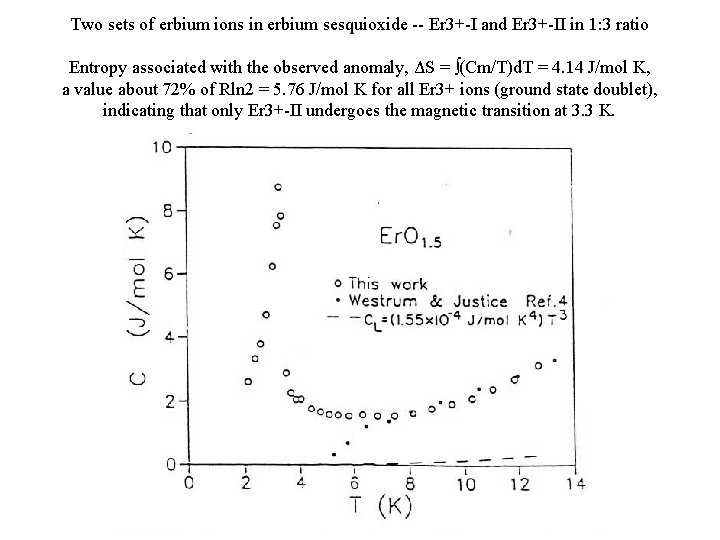
Two sets of erbium ions in erbium sesquioxide -- Er 3+-I and Er 3+-II in 1: 3 ratio Entropy associated with the observed anomaly, ΔS = ∫(Cm/T)d. T = 4. 14 J/mol K, a value about 72% of Rln 2 = 5. 76 J/mol K for all Er 3+ ions (ground state doublet), indicating that only Er 3+-II undergoes the magnetic transition at 3. 3 K.

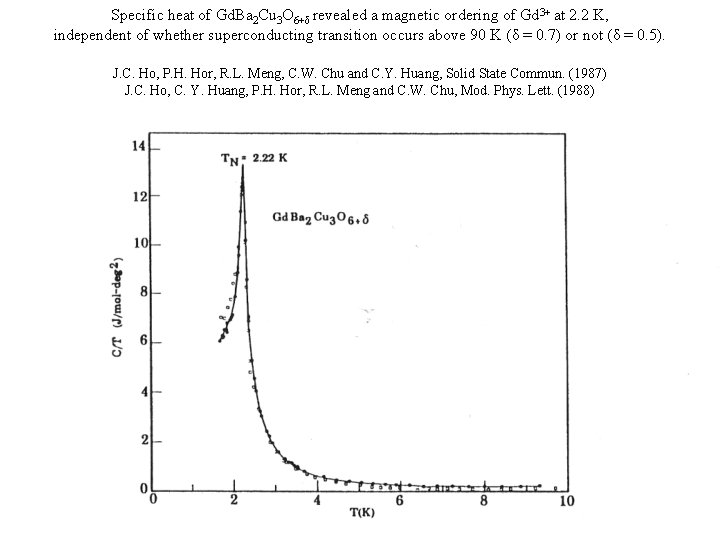
Specific heat of Gd. Ba 2 Cu 3 O 6+δ revealed a magnetic ordering of Gd 3+ at 2. 2 K, independent of whether superconducting transition occurs above 90 K (δ = 0. 7) or not (δ = 0. 5). J. C. Ho, P. H. Hor, R. L. Meng, C. W. Chu and C. Y. Huang, Solid State Commun. (1987) J. C. Ho, C. Y. Huang, P. H. Hor, R. L. Meng and C. W. Chu, Mod. Phys. Lett. (1988)

President Ronald Reagan gave the keynote address at the Conference on “Superconductivity: Challenge for the future”, Washington, D. C. , July 1987.

Specific heat and entropy in chemical thermodynamics Low temperature specific heat in solid state physics Phonon (lattice) Conduction electrons Nuclear magnetic moments Critical phenomena Superconductivity Magnetic transitions Some applications to materials science Magnetic clusters Electron localization Non-uniform superconductors Nano-size effect

Physical Review (1893) Physical Review B -- Solid State Physics (1970) Physical Review B – Condensed Matter (1978) Physical Review B -- Condensed Matter and Materials Physics

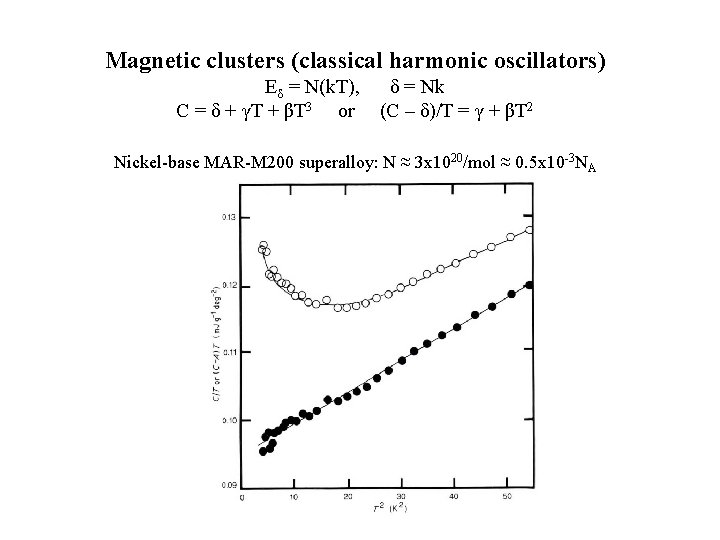
Magnetic clusters (classical harmonic oscillators) Eδ = N(k. T), δ = Nk C = δ + γT + βT 3 or (C – δ)/T = γ + βT 2 Nickel-base MAR-M 200 superalloy: N ≈ 3 x 1020/mol ≈ 0. 5 x 10 -3 NA

Professor Sir John Enderby Kt, CBE, Ph. D (London), DSc (Lough), FInst. P, FRS Vice President of Royal Society, 1999 -2004 President of Institute of Physics, 2004 -2006

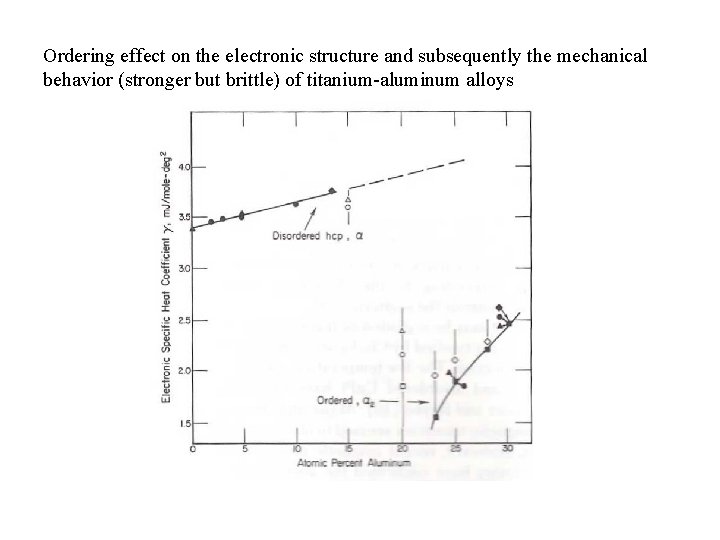
Ordering effect on the electronic structure and subsequently the mechanical behavior (stronger but brittle) of titanium-aluminum alloys

Light and strong Al-Li alloys Large electronegativity difference: 1. 47 for Al and 0. 97 for Li Intermetallic compound Al. Li has its m. p (700 o. C) extruding into the liquidus.

Detection of superconducting transitions Transport property measurements (qualitative): Electrical resistivity (impurity forming a continuous network? ) Thermodynamic property measurements (quantitative): Magnetic susceptibility (shielding effect? ) Specific heat (qualitative) fraction of superconducting component in sample (BCS theory: (Ces/γT)Tc ≈ 2. 43)

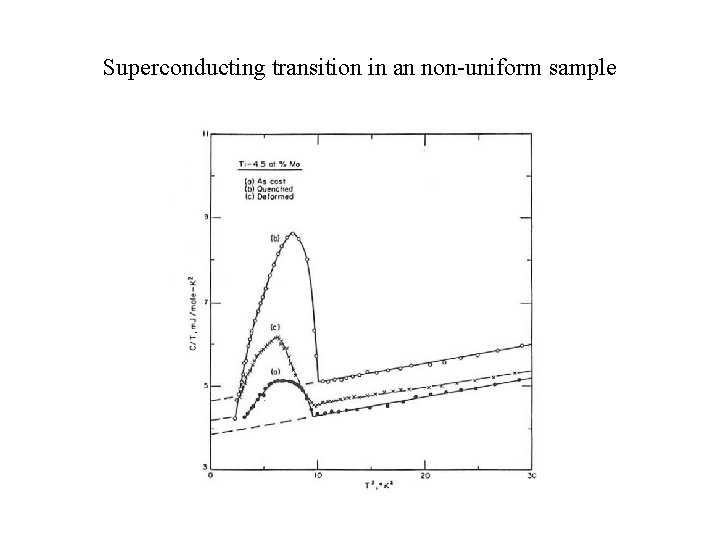
Superconducting transition in an non-uniform sample

Specific heat and entropy in chemical thermodynamics Low temperature specific heat in solid state physics Phonon (lattice) Conduction electrons Nuclear magnetic moments Critical phenomena Superconductivity Magnetic transitions Some applications to materials science Magnetic clusters Electron localization Non-uniform superconductors Nano-size effect

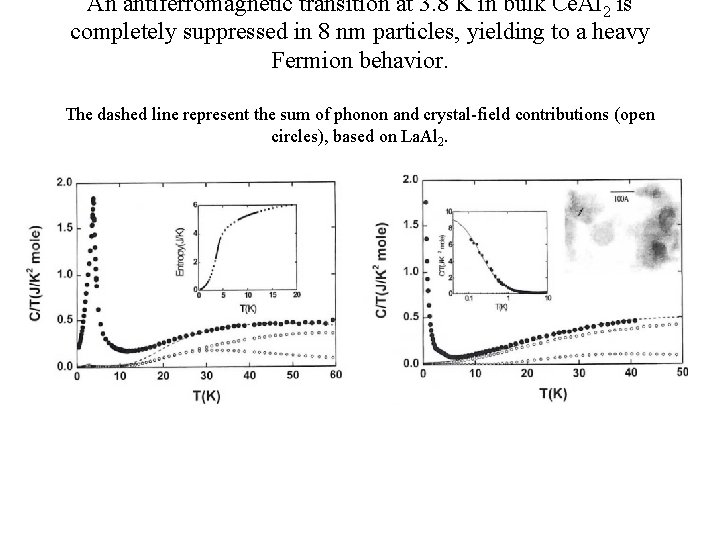
An antiferromagnetic transition at 3. 8 K in bulk Ce. Al 2 is completely suppressed in 8 nm particles, yielding to a heavy Fermion behavior. The dashed line represent the sum of phonon and crystal-field contributions (open circles), based on La. Al 2.

In conclusion, measurements of low temperature specific heat, as a thermodynamic quantity, provide some fundamental information about a solid, as well as a relatively simple and effective evaluation technique in materials science.