Low Complexity Virtual Antenna Arrays Using Cooperative Relay

Low Complexity Virtual Antenna Arrays Using Cooperative Relay Selection Aggelos Bletsas, Ashish Khisti, and Moe Z. Win Laboratory for Information and Decision Systems (LIDS) Massachusetts Institute of Technology moewin@mit. edu

Outline ü Motivation ü System Model ü Protocols with Cooperative Relay Selection ü ü ü Zero-Feedback Single-Bit Feedback (single or multiple rounds) Concluding Remarks 2

Motivation (1) ü Cooperative communications Node cooperation to improve the performance of wireless networks by coordination of terminals distributed in space. 3

Motivation (2) ü Cooperation has been widely viewed as a distributed, multiple relay, transmission problem: Ø Using distributed Phased-array techniques Ø or Using distributed Space-Time Coding ü Phased-array techniques require tracking and control of multiple carrier-phase differences ü Space-Time Coding for multiple antennas is an open area of research ü Both become less practical due to the distributed nature of the Relay Channel ü Both increase the complexity and cost of the transceiver. 4

Motivation (3) ü Phased Array and Space-Time Coding Techniques increase the complexity and cost of the transceiver Simplification of cooperative communication to minimize the required hardware complexity and cost “Distributed single-relay selection” “Can we achieve globally optimal cooperation simply by single-relay transmission? ” 5

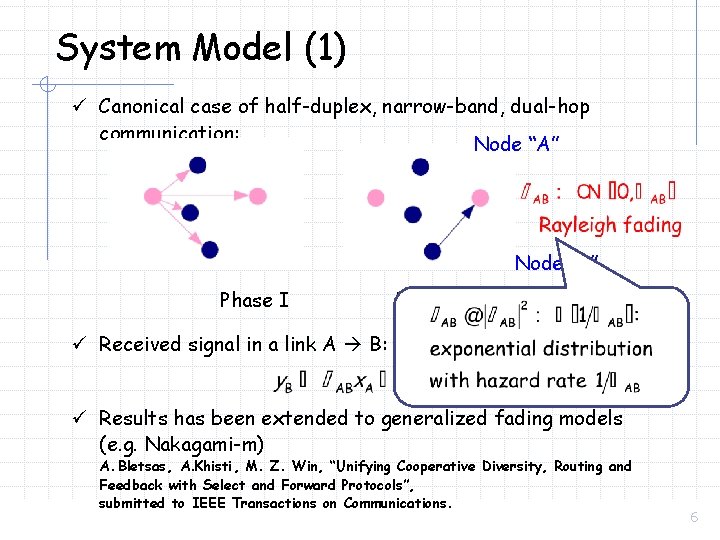
System Model (1) ü Canonical case of half-duplex, narrow-band, dual-hop communication: Node “A” Node “B” Phase II ü Received signal in a link A B: ü Results has been extended to generalized fading models (e. g. Nakagami-m) A. Bletsas, A. Khisti , M. Z. Win, “Unifying Cooperative Diversity, Routing and Feedback with Select and Forward Protocols”, submitted to IEEE Transactions on Communications. 6

System Model (2) ü Performance metric: Diversity order-multiplexing gain tradeoff (DMT) : Outage Probability as a function of rate, SNR : Rate ü DMT averages out relay topology : SNR (high SNR tool) ü DMT simplifies analysis : Rate as a function of SNR : SNR ü Diversity order reliability ü Multiplexing gain achievable throughput (degrees of freedom) 7

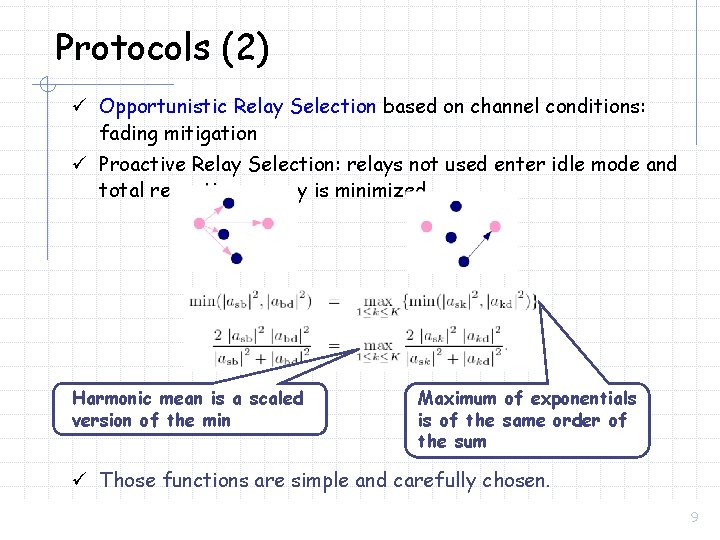
Protocols (1) ü Key idea 1: among a set of K possible relays, only one will be used ü Key idea 2: the selected, “best” relay will be chosen before source transmission (Proactive Relay selection) ü Key idea 3: the selected relay will be used only if needed (feedback availability) ü Which is the “best” relay to use? Select the relay that maximizes a function of the end-to-end channel conditions: ü 2 Opportunistic functions: min vs harmonic mean 8

Protocols (2) ü Opportunistic Relay Selection based on channel conditions: fading mitigation ü Proactive Relay Selection: relays not used enter idle mode and total reception energy is minimized Harmonic mean is a scaled version of the min Maximum of exponentials is of the same order of the sum ü Those functions are simple and carefully chosen. 9

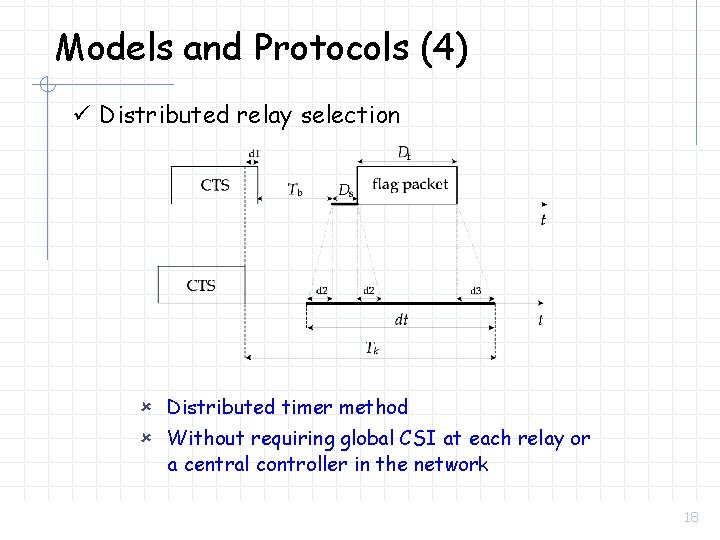
Protocols (3) ü Distributed relay selection: to find out the max element in a set, you don’t need to know the individual value of all elements in the set. Ø Ø Distributed timer method has been proposed, analyzed and implemented in simple radios. Without requiring global CSI at each relay or at a central controller in the network. A. Bletsas, “Intelligent Antenna Sharing in Cooperative Diversity Wireless Networks”, Ph. D. Dissertation, Massachusetts Institute of Technology, September 2005. ü Intuition: to select the tallest student in a classroom, you don’t need to measure each of them, but instead ask all of them to stand up and have the tallest observe the class and raise her hand. 10

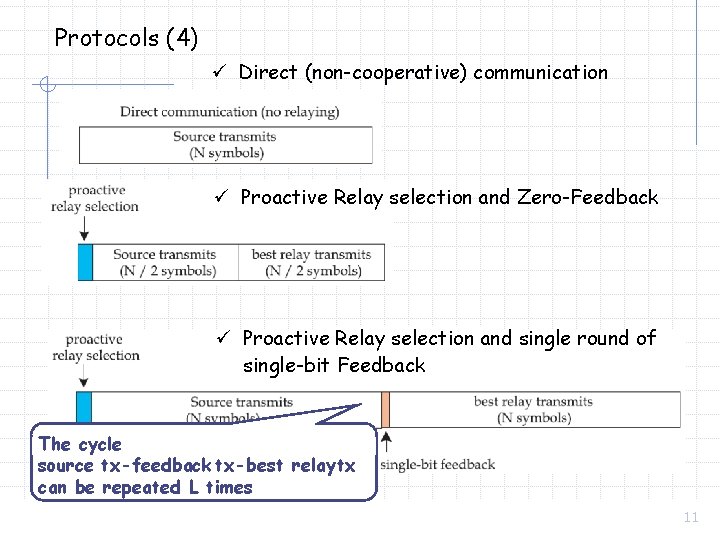
Protocols (4) ü Direct (non-cooperative) communication ü Proactive Relay selection and Zero-Feedback ü Proactive Relay selection and single round of single-bit Feedback The cycle source tx-feedback tx-best relay tx can be repeated L times 11

Discussion ü Proactive relay selection ü Simplify the receiver design and the overall network operation (which is equivalent to routing). ü May seem that selecting a single relay before the source transmission would degrade performance. ü Single relay transmission ü May seem that a single relay transmission would degrade performance. Results show that there is no performance loss! 12

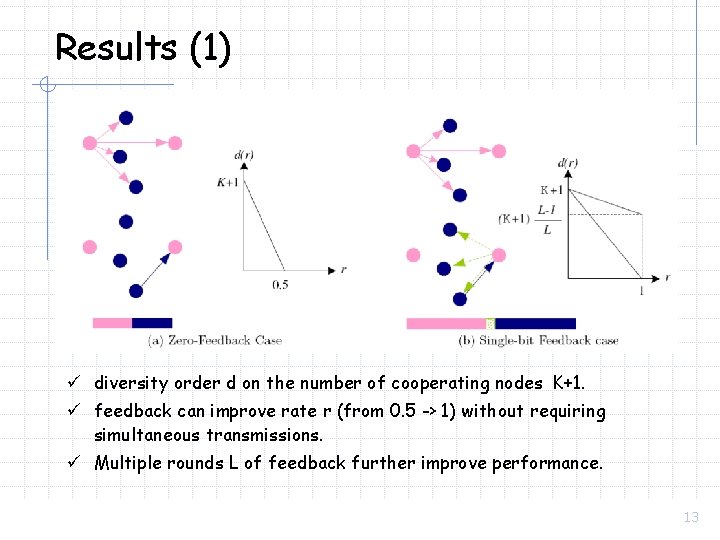
Results (1) ü diversity order d on the number of cooperating nodes K+1. ü feedback can improve rate r (from 0. 5 -> 1) without requiring simultaneous transmissions. ü Multiple rounds L of feedback further improve performance. 13

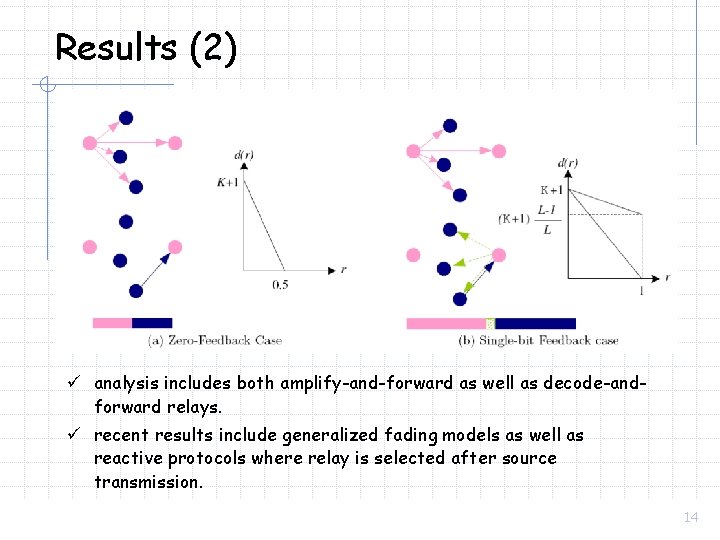
Results (2) ü analysis includes both amplify-and-forward as well as decode-andforward relays. ü recent results include generalized fading models as well as reactive protocols where relay is selected after source transmission. 14

Concluding Remarks (1) ü Put forth simple opportunistic relay selection rules for decode-and-forward (Da. F) or amplify-and-forward relays and provided DMT analysis. ü Studied the impact of feedback with multiple relays. ü Showed that single relay selection is equivalent to complex space-time coding, even though simpler. ü Proactive opportunistic relaying reduces the reception energy cost in the network. Ø Energy-efficient routing 15

Concluding Remarks (2) ü Our results reveal that relays in cooperative communications can be viewed not only as active re -transmitters but also as distributed sensors of the wireless channel. Ø Ø Cooperative relays can be useful even when they do not transmit, provided that they cooperatively listen. Cooperation benefits can be cultivated with simple radio implementation. 16

Thank You! ü This research was supported, in part, by ü The Office of Naval Research Young Investigator Award N 00014 -03 -1 -0489, ü The National Science Foundation under Grant ANI-0335256, ü The Charles Stark Draper Laboratory Robust Distributed Sensor Networks Program 17

Models and Protocols (4) ü Distributed relay selection û Distributed timer method û Without requiring global CSI at each relay or a central controller in the network 18