Lossless Compression Statistical Model Part II Arithmetic Coding

Lossless Compression Statistical Model Part II Arithmetic Coding 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 1

CONTENTS n n n Introduction to Arithmetic Coding & Decoding Algorithm Generating a Binary Code for Arithmetic Coding Higher-order and Adaptive Modeling Applications of Arithmetic Coding 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 2

Arithmetic Coding n Huffman codes have to be an integral number of bits long, while the entropy value of a symbol is almost always a faction number, theoretical possible compressed message cannot be achieved. n 2021/5/21 For example, if a statistical method assign 90% probability to a given character, the optimal code size would be 0. 15 bits. 資料壓縮 ※Unit 4 Arithmetic Coding※ 3

Arithmetic Coding n n Arithmetic coding bypasses the idea of replacing an input symbol with a specific code. It replaces a stream of input symbols with a single floatingpoint output number. Arithmetic coding is especially useful when dealing with sources with small alphabets, such as binary sources, and alphabets with highly skewed probabilities. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 4

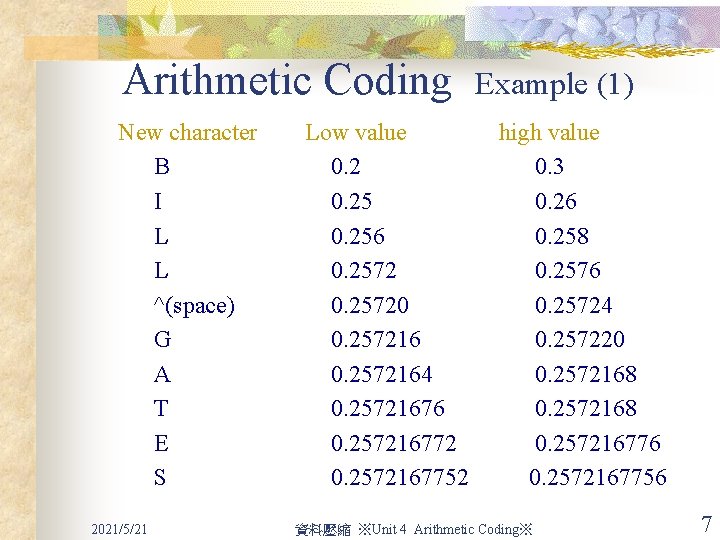
Arithmetic Coding Character probability ^(space) 1/10 A 1/10 B 1/10 E 1/10 G 1/10 I 1/10 L 2/10 S 1/10 T 1/10 Example (1) Range Suppose that we want to encode the message BILL GATES 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 5

Arithmetic Coding 0. 0 0. 1 ^ 0. 2 A 0. 3 B 0. 4 E 0. 5 G 0. 6 I 0. 2 2021/5/21 0. 256 0. 25724 0. 25 I 0. 26 L 0. 8 0. 9 S 1. 0 T 0. 25 Example (1) 0. 3 ^ 0. 2572 0. 256 0. 258 0. 2572 L 0. 26 L 0. 2576 0. 258 資料壓縮 ※Unit 4 Arithmetic Coding※ 0. 2576 6

Arithmetic Coding New character B I L L ^(space) G A T E S 2021/5/21 Low value 0. 256 0. 25720 0. 2572164 0. 25721676 0. 257216772 0. 2572167752 Example (1) high value 0. 3 0. 26 0. 258 0. 2576 0. 25724 0. 257220 0. 2572168 0. 257216776 0. 2572167756 資料壓縮 ※Unit 4 Arithmetic Coding※ 7

Arithmetic Coding n n Example (1) The final value, named a tag, 0. 2572167752 will uniquely encode the message ‘BILL GATES’. Any value between 0. 2572167752 and 0. 2572167756 can be a tag for the encoded message, and can be uniquely decoded. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 8

Arithmetic Coding n Encoding algorithm for arithmetic coding. Low = 0. 0 ; high =1. 0 ; while not EOF do range = high - low ; read(c) ; high = low + range high_range(c) ; low = low + range low_range(c) ; enddo output(low); 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 9

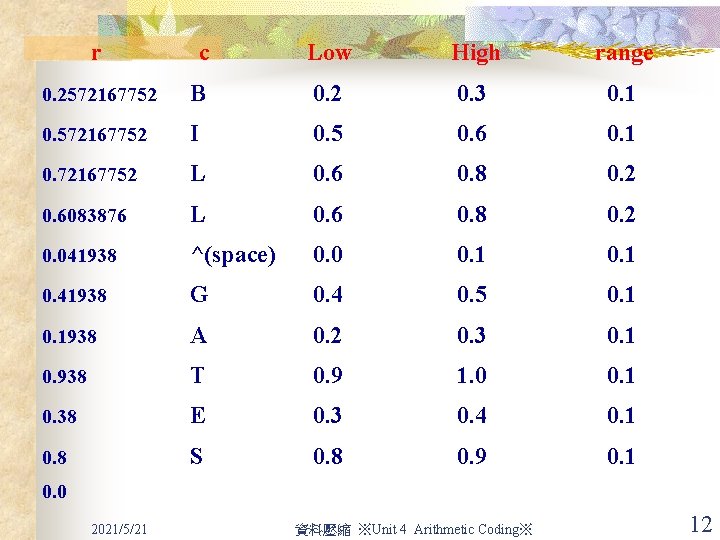
Arithmetic Coding n Decoding is the inverse process. n Since 0. 2572167752 falls between 0. 2 and 0. 3, the first character must be ‘B’. n Removing the effect of ‘B’ from 0. 2572167752 by first subtracting the low value of B, 0. 2, giving 0. 0572167752. n Then divided by the width of the range of ‘B’, 0. 1. This gives a value of 0. 572167752. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 10

Arithmetic Coding n n Then calculate where that lands, which is in the range of the next letter, ‘I’. The process repeats until 0 or the known length of the message is reached. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 11

r c Low High range 0. 2572167752 B 0. 2 0. 3 0. 1 0. 572167752 I 0. 5 0. 6 0. 1 0. 72167752 L 0. 6 0. 8 0. 2 0. 6083876 L 0. 6 0. 8 0. 2 0. 041938 ^(space) 0. 0 0. 1 0. 41938 G 0. 4 0. 5 0. 1938 A 0. 2 0. 3 0. 1 0. 938 T 0. 9 1. 0 0. 1 0. 38 E 0. 3 0. 4 0. 1 0. 8 S 0. 8 0. 9 0. 1 0. 0 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 12

Arithmetic Coding n Decoding algorithm r = input_code repeat search c such that r falls in its range ; output(c) ; r = r - low_range(c) ; r = r/(high_range(c) - low_range(c)); until r equal 0 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 13

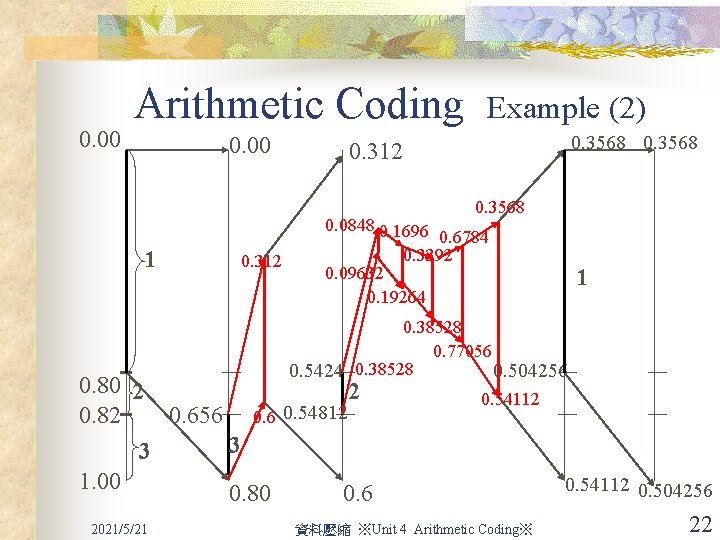
Arithmetic Coding Example (2) Suppose that we want to encode the message 1321 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 14

0. 00 Arithmetic Coding 0. 00 0. 656 1 0. 7712 0. 773504 0. 80 2 2 0. 77408 0. 82 0. 656 3 3 1. 00 0. 80 2021/5/21 Example (2) 0. 77408 資料壓縮 ※Unit 4 Arithmetic Coding※ 0. 773504 15

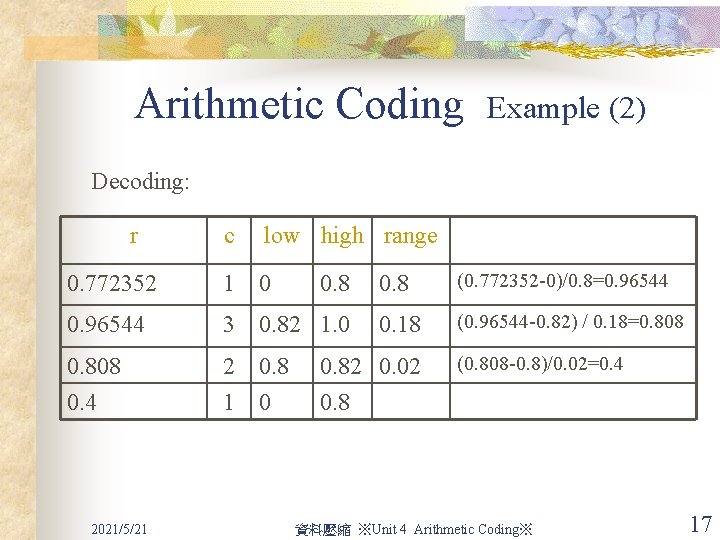
Arithmetic Coding Example (2) Encoding: New character 1 3 2 1 2021/5/21 Low value 0. 0 0. 656 0. 7712 High value 1. 0 0. 800 0. 77408 0. 773504 資料壓縮 ※Unit 4 Arithmetic Coding※ 16

Arithmetic Coding Example (2) Decoding: r c low high range 0. 772352 1 0 0. 96544 3 0. 82 1. 0 0. 808 0. 4 2 0. 8 1 0 2021/5/21 0. 8 (0. 772352 -0)/0. 8=0. 96544 0. 18 (0. 96544 -0. 82) / 0. 18=0. 808 0. 82 0. 02 0. 8 (0. 808 -0. 8)/0. 02=0. 4 資料壓縮 ※Unit 4 Arithmetic Coding※ 17

Arithmetic Coding n n n In summary, the encoding process is simply one of narrowing the range of possible numbers with every new symbol. The new range is proportional to the predefined probability attached to that symbol. Decoding is the inverse procedure, in which the range is expanded in proportion to the probability of each symbol as it is extracted. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 18

Arithmetic Coding n n n Coding rate approaches high-order entropy theoretically. Not so popular as Huffman coding because , are needed. Average bits/byte on 14 files (program, object, text, and etc. ) Huff. LZW 4. 99 4. 71 2021/5/21 LZ 77/LZ 78 2. 95 資料壓縮 ※Unit 4 Arithmetic Coding※ Arithmetic 2. 48 19

Generating a Binary Code for Arithmetic Coding n Problem: The binary representation of some of the generated floating point values (tags) would be infinitely long. We need increasing precision as the length of the sequence increases. n Solution: Synchronized rescaling and incremental encoding. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 20

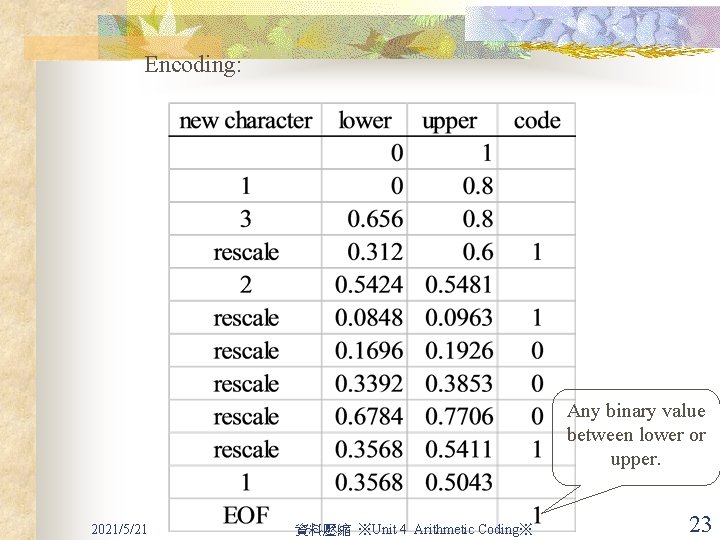
Generating a Binary Code for Arithmetic Coding n n n If the upper bound and the lower bound of the interval are both less than 0. 5, then rescaling the interval and transmitting a ‘ 0’ bit. If the upper bound and the lower bound of the interval are both greater than 0. 5, then rescaling the interval and transmitting a ‘ 1’ bit. Mapping rules: 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 21

0. 00 Arithmetic Coding 0. 00 0. 3568 0. 312 0. 0848 0. 1696 1 0. 312 Example (2) 0. 3568 0. 6784 0. 3392 0. 09632 0. 19264 1 0. 38528 0. 77056 0. 5424 0. 38528 0. 504256 0. 80 2 2 0. 82 0. 656 0. 54812 3 3 1. 00 0. 80 0. 6 2021/5/21 0. 54112 資料壓縮 ※Unit 4 Arithmetic Coding※ 0. 54112 0. 504256 22

Encoding: Any binary value between lower or upper. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 23

n Decoding the bit stream start with 1100011… n The number of bits to distinct the different symbol is bits. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 24

Higher-order and Adaptive Modeling n To have a good compression ratio results in the statistical model compression methods, the model should be n n n Accurately predicts the frequency/ probability of symbols in the data stream. A non-uniform distribution The finite context modeling provide a better prediction ability. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 25

Higher-order and Adaptive Modeling n Finite context modeling : n Calculate the probabilities for each incoming symbol based on the context (上下文) in which the symbol appears. n n The order of the model refers to the number of previous symbols that make up the context. n n 2021/5/21 e. g. In information theory, this type of finite context modeling is called Markov process/system. 資料壓縮 ※Unit 4 Arithmetic Coding※ 26

Higher-order and Adaptive Modeling n Problem: n n n As the order of the model increases linearly, the memory consumed by the model increases exponentially. e. g. for q symbols and order k, the table size will be qk. Solution: n 2021/5/21 Adaptive modeling 資料壓縮 ※Unit 4 Arithmetic Coding※ 27

Higher-order and Adaptive Modeling n Adaptive modeling n n n 2021/5/21 In adaptive data compression, both the compressor and decompressor start with the same model. The compressor encodes a symbol using the existing model, then it updates the model to account for the new symbol. The decompressor likewise decodes a symbol using the existing model, then it updates the model. 資料壓縮 ※Unit 4 Arithmetic Coding※ 28

Higher-order and Adaptive Modeling n n n Adaptive data compression has a slight disadvantage in that it starts compressing with less than optimal statistics. By subtracting the cost of transmitting the statistics with the compressed data, however, an adaptive algorithm will usually perform better than a fixed statistical model. Adaptive compression also suffers in the cost of updating the model. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 29

n Higher-order and Adaptive Modeling Encoding phase low = 0. 0 ; high = 1. 0 ; while not EOF do read(c) ; range = high - low ; high = low + range *high_ range(context, c); low = low + range *low_ range(context, c); update_model(context, c); context = c ; enddo output(low); 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 30

Higher-order and Adaptive Modeling n Instead of just having a single context table, we now have a set of q context tables. n Every symbol is encoded using the context table from the previously seen symbol, and only the statistics for the selected context get updated after the symbol is seen. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 31

Higher-order and Adaptive Modeling n Decoding phase r = input_code ; repeat search c from context_table [context] s. t. r falls in its range ; output(c) ; range = high_ range(context, c) - low_ range(context, c) ; r = r/ range ; update_model(context, c) ; context = c ; until r equal 0. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 32

Applications The JBIG Standard JBIG --- Joint Bi-Level Image Processing Group JBIG was issued in 1993 by ISO/IEC for the progressive lossless compression of binary and low-precision gray-level images (typically, having less than 6 bits/pixel). The major advantages of JBIG over other existing standards are its capability of progressive encoding and its superior compression efficiency. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 33

The JBIG Standard Context-based arithmetic coder The core of JBIG is an adaptive context-based arithmetic coder. If the probability of encountering a black pixel p is 0. 2 and the probability of encountering a white pixel q is 0. 8. Using a single arithmetic coder, the entropy is 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 34

The JBIG Standard Context-based arithmetic coder Group the data into Set A (80%) and Set B (20%), using two coders pw = 0. 95, pb = 0. 05, HA = 0. 286 pw = 0. 3, pb = 0. 7, HB = 0. 881, then, the average H = HA *. 8+HB *. 2 = 0. 405. The number of possible patterns is 1024. The JBIG coder uses 1024 or 4096 coders Pixel to be coded 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 35

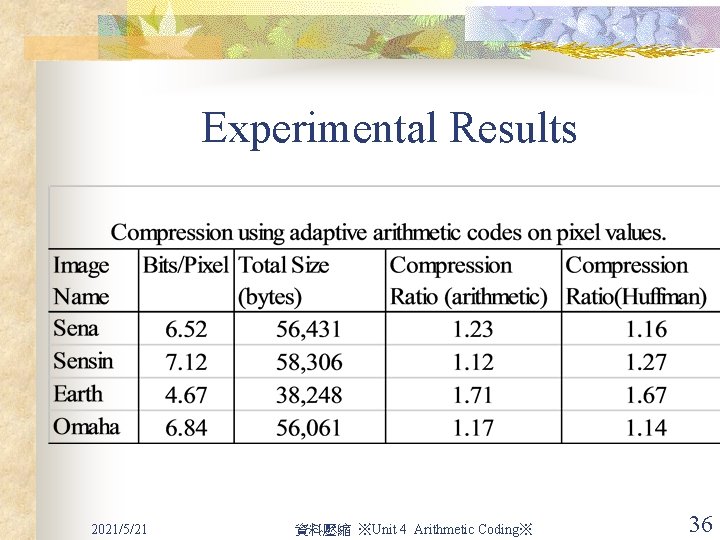
Experimental Results 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 36

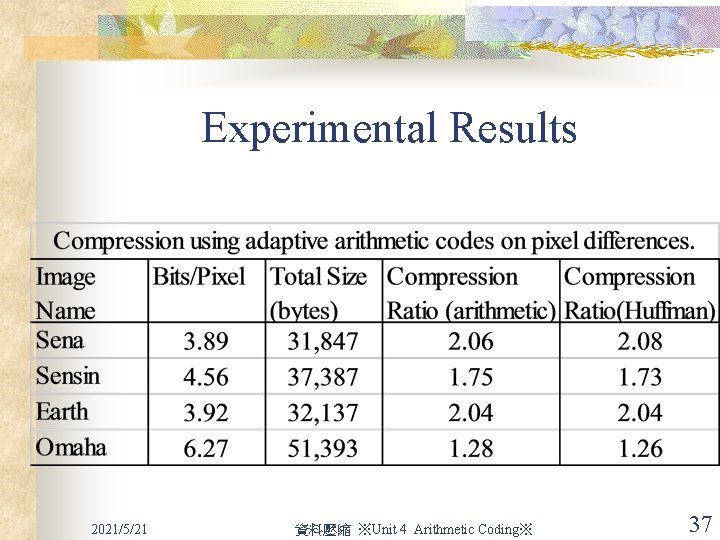
Experimental Results 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 37

Conclusions n Compression-ratio tests show that statistical modeling can perform at least as well as dictionary - based methods. But the high order programs are at present somewhat impractical because of their resource requirements. n JPEG, MPEG-1/2 uses Huffman and arithmetic coding – preprocessed by DPCM n JPEG-LS n JPEG 2000, MPEG-4 uses arithmetic coding only n Order-3 : the best performance for Unix. 2021/5/21 資料壓縮 ※Unit 4 Arithmetic Coding※ 38