Lossless Compression of FloatingPoint Geometry Martin Isenburg Peter

Lossless Compression of Floating-Point Geometry Martin Isenburg Peter Lindstrom Jack Snoeyink UNC Chapel Hill LLNL Livermore UNC Chapel Hill

Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Meshes and Compression • connectivity face 1 1 2 3 face 2 2 1 4 3 m * 32 bits face 3 3 2 5 146 MB 3 MB facem • geometry vertex 1 ( x, y, z ) 127 MB vertex ( x, y, z ) 2 3 n * 32 bits vertex 3 ( x, y, z ) 25 MB vertexn 20 uniform quantization UNC power-plant 12, 748, 510 11, 070, 509 triangles vertices

Floating-Point Numbers • have varying precision • largest exponent least precise 23 bits of precision 0 4 8 16 32 64 23 bits of precision 128 x - axis - 4. 095 190. 974

Samples per Millimeter 16 bit 18 bit 327 1311 2. 7 m 20 bit 22 bit 24 bit 20 cm 97 388 1553 195 m 5 22 86

No quantizing possible … • stubborn scientists / engineers – “Do not touch my data !!!” • data has varying precision – specifically aligned with origin • not enough a-priori information – no bounding box – unknown precision – streaming data source

Mesh Compression • Geometry Compression [[Deering, 95] – Fast Rendering – Progressive Transmission – Maximum. Compression

Mesh Compression • Geometry Compression [[Deering, 95] – Fast Rendering – Progressive Transmission – Maximum. Compression • Connectivity • Geometry

Mesh Compression • Geometry Compression [[Deering, 95] – Fast Rendering – Progressive Transmission – Maximum. Compression • Connectivity • Geometry – lossy – lossless

Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Geometry Compression • Classic approaches [95 – 98]: – linear prediction Geometry Compression Java 3 D [Deering, 95] Geometric Compression through topological surgery [Taubin & Rossignac, 98] MPEG - 4 Triangle Mesh Compression Virtue 3 D [Touma & Gotsman, 98]

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral re-meshing space-dividing vector-quantization angle-based delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral Spectral Compression of Mesh Geometry re-meshing [Karni & Gotsman, 00] space-dividing vector-quantization angle-based expensive numerical computations delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral Progressive Geometry Compression re-meshing [Khodakovsky et al. , 00] space-dividing vector-quantization angle-based modifies mesh prior to compression delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral Geometric Compression for interactive transmission re-meshing [Devillers & Gandoin, 00] space-dividing vector-quantization angle-based poly-soups; complex geometric algorithms delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral Vertex data compression for triangle meshes re-meshing [Lee & Ko, 00] space-dividing vector-quantization angle-based local coord-system + vector-quantization delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral Angle-Analyzer: A trianglequad mesh codec re-meshing [Lee, Alliez & Desbrun, 02] space-dividing vector-quantization angle-based dihedral + internal = heavy trigonometry delta coordinates

Geometry Compression • Classic approaches [95 – 98]: – linear prediction • Recent approaches [00 – 03]: – – – spectral High-Pass Quantization for Mesh Encoding re-meshing [Sorkine et al. , 03] space-dividing vector-quantization angle-based basis transformation with Laplacian matrix delta coordinates

Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Predictive Coding 1. 2. 3. 4. quantize positions with b bits predict from neighbors compute difference compress with entropy coder floating point (1. 314, -0. 204, 0. 704) integer (1008, 68, 718)

Predictive Coding 1. 2. 3. 4. quantize positions with b bits predict from neighbors compute difference compress with entropy coder prediction rule prediction (1004, 71, 723) prediction rule prediction (1. 276, -0. 182, 0. 734)

Predictive Coding 1. 2. 3. 4. quantize positions with b bits predict from neighbors compute difference compress with entropy coder position (1008, 68, 718) prediction (1004, 71, 723) position (1. 314, -0. 204, 0. 704) corrector (4, -3, -5) prediction (1. 276, -0. 182, 0. 734) ?

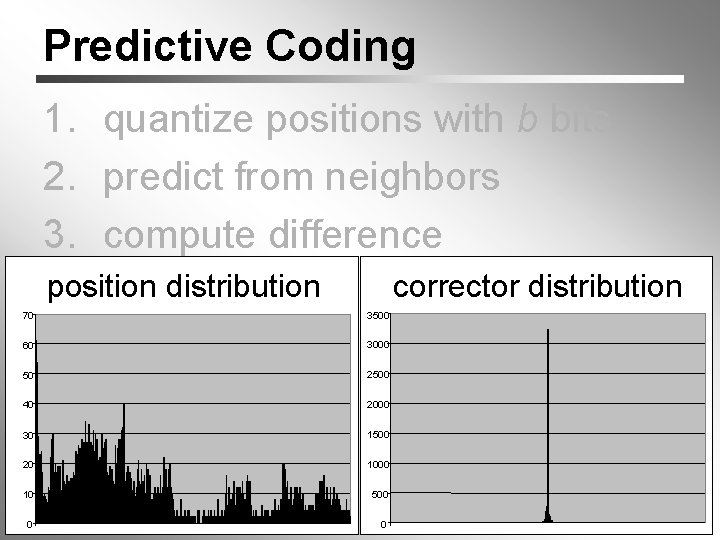
Predictive Coding 70 1. quantize positions with b bits 2. predict from neighbors 3. compute difference position distribution correctorcoder distribution 4. compress with entropy 3500 60 3000 50 2500 40 2000 30 1500 20 1000 10 500 0 0

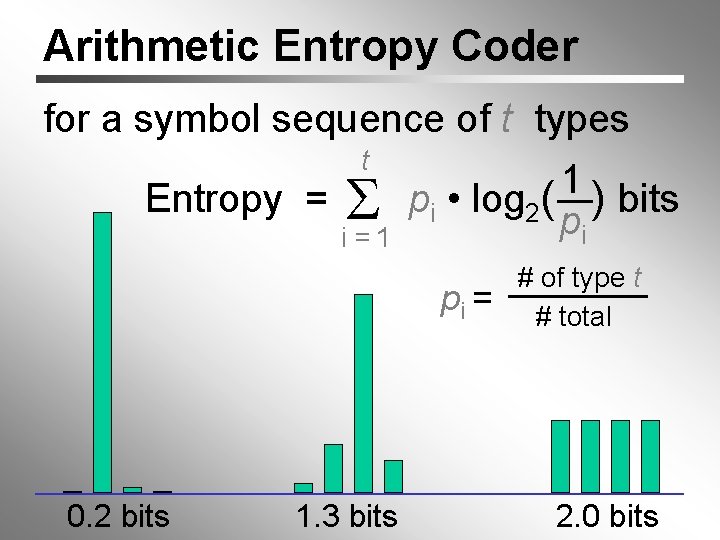
Arithmetic Entropy Coder for a symbol sequence of t types Entropy = t i =1 1 pi • log 2( ) bits pi pi = 0. 2 bits 1. 3 bits # of type t # total 2. 0 bits

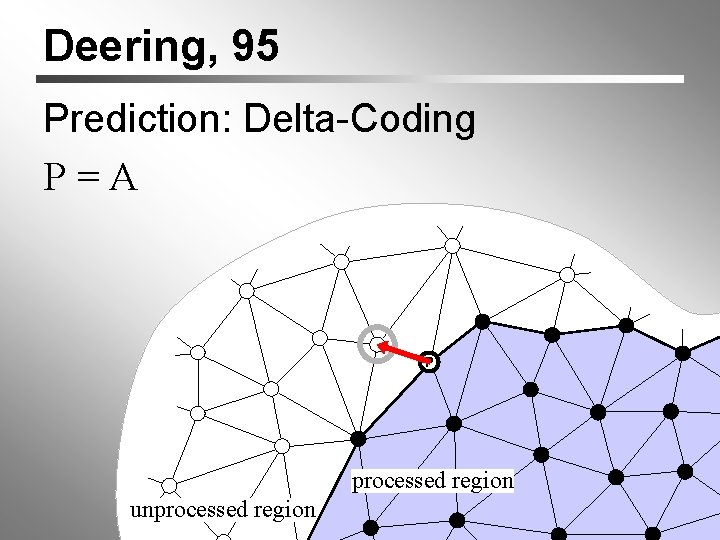
Deering, 95 Prediction: Delta-Coding P=A P A processed region unprocessed region

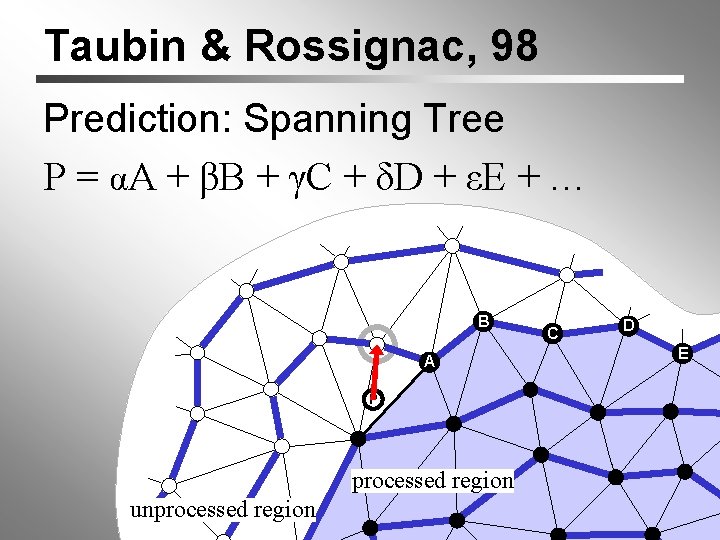
Taubin & Rossignac, 98 Prediction: Spanning Tree P = αA + βB + γC + δD + εE + … B A P processed region unprocessed region C D E

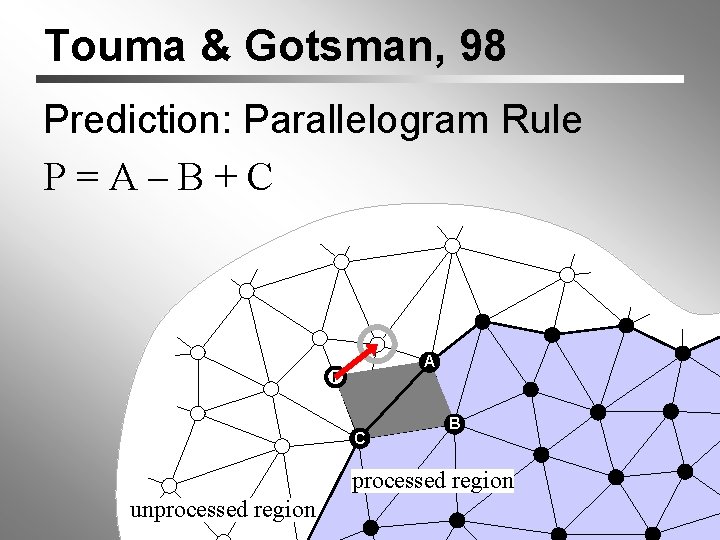
Touma & Gotsman, 98 Prediction: Parallelogram Rule P=A–B+C A P C B processed region unprocessed region

Talk Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Corrective Vectors ? position (1008, 68, 718) prediction (1004, 71, 723) compute difference vector with integer arithmetic position (1. 314, -0. 204, 0. 704) compute difference vector with floating-point arithmetic ? corrector (4, -3, -5) prediction (1. 276, -0. 182, 0. 734) corrector (0. 038, -0. 022, -0. 030)

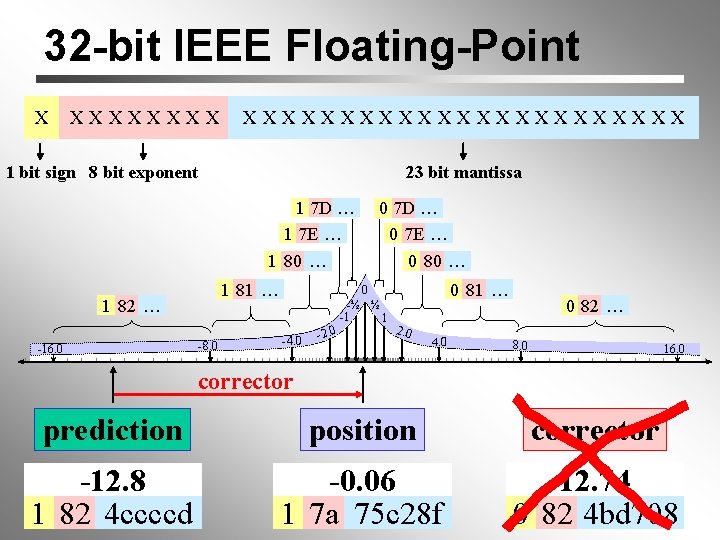
32 -bit IEEE Floating-Point X XXXXXXXXXXXXXXX 1 bit sign 8 bit exponent 23 bit mantissa 1 7 D … 1 7 E … 0 7 D … 0 7 E … 1 80 … 1 81 … 1 82 … -16. 0 - 8. 0 0 80 … 0 81 … 0 -½ ½ -1 1 - 4. 0 - 2. 0 4. 0 0 82 … 8. 0 16. 0 corrector prediction position corrector -12. 8 1 82 4 ccccd -0. 06 1 7 a 75 c 28 f 12. 74 0 82 4 bd 708

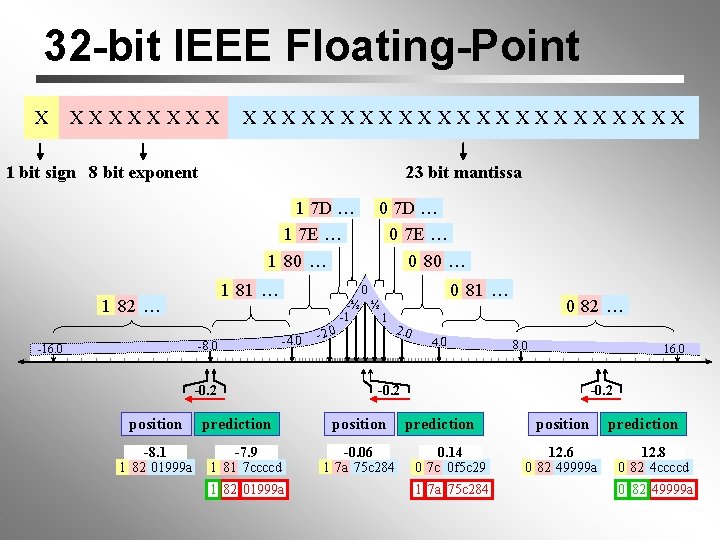
32 -bit IEEE Floating-Point X XXXXXXXXXXXXXXX 1 bit sign 8 bit exponent 23 bit mantissa 1 7 D … 1 7 E … 0 7 D … 0 7 E … 1 80 … 1 81 … 1 82 … - 8. 0 -16. 0 -8. 1 1 82 01999 a 0 81 … 0 -½ ½ -1 1 - 4. 0 -0. 2 position 0 80 … prediction -7. 9 1 81 7 ccccd 1 82 01999 a - 2. 0 4. 0 0 82 … 8. 0 16. 0 -0. 2 position -0. 06 1 7 a 75 c 284 -0. 2 prediction 0. 14 0 7 c 0 f 5 c 29 1 7 a 75 c 284 position 12. 6 0 82 49999 a prediction 12. 8 0 82 4 ccccd 0 82 49999 a

Floating-Point Corrections (1) 0 position prediction 12. 6 0 82 49999 a 12. 8 0 82 4 ccccd 82 49999 a 0 compress 82 0 49999 a 0 4 ccccd 0 -033333 82 4 ccccd use context 82

Floating-Point Corrections (2) 1 position prediction -8. 1 1 82 01999 a -7. 9 1 81 7 ccccd 82 01999 a 1 compress 82 1 01999 a 0 1 0 01999 a 81 7 ccccd use context 81 use context 82

Floating-Point Corrections (3) 1 position prediction -0. 06 1 7 a 75 c 284 0. 14 0 7 c 0 f 5 c 29 7 a 75 c 284 0 compress 7 a 1 75 c 284 1 0 0 75 c 284 7 c 0 f 5 c 29 use context 7 c use context 7 a

Talk Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Results [bpv] model buddha david power plant lucy raw gzip -9 ours ratio 96. 0 55. 8 56. 1 23. 7 78. 7 49. 9 34. 7 29. 1 44. 4 0. 90 0. 62 1. 21 0. 56

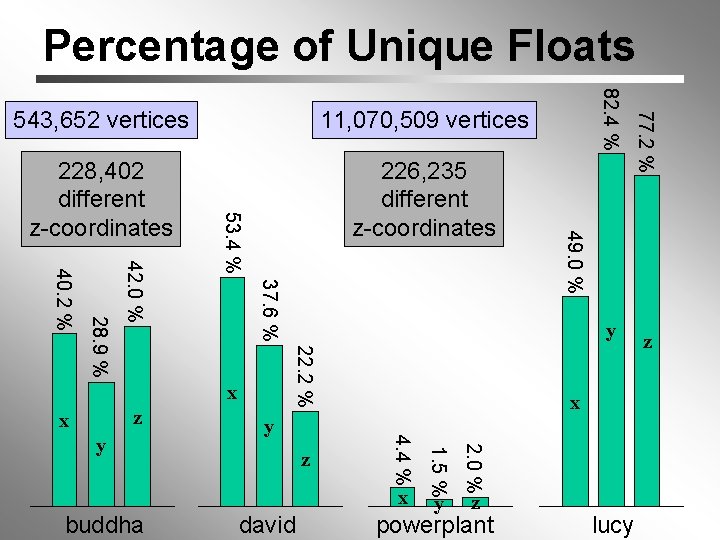
Percentage of Unique Floats 37. 6 % 42. 0 % z x y buddha david y 2. 0 % x 1. 5 % z x 4. 4 % y y 22. 2 % 28. 9 % 40. 2 % x z powerplant 77. 2 % 226, 235 different z-coordinates 82. 4 % 228, 402 different z-coordinates 49. 0 % 11, 070, 509 vertices 53. 4 % 543, 652 vertices lucy z

Completing, not competing !!! model buddha david power plant lucy bit-rate [bpv] 16 bit 20 bit 24 bit lossless 21. 8 12. 5 11. 6 14. 6 32. 2 23. 2 18. 5 26. 5 44. 0 34. 1 24. 2 39. 1 49. 9 34. 7 29. 1 44. 4 compression ratio [%] buddha david power plant lucy 45 26 24 30 54 39 31 44 61 47 34 54 52 36 30 46

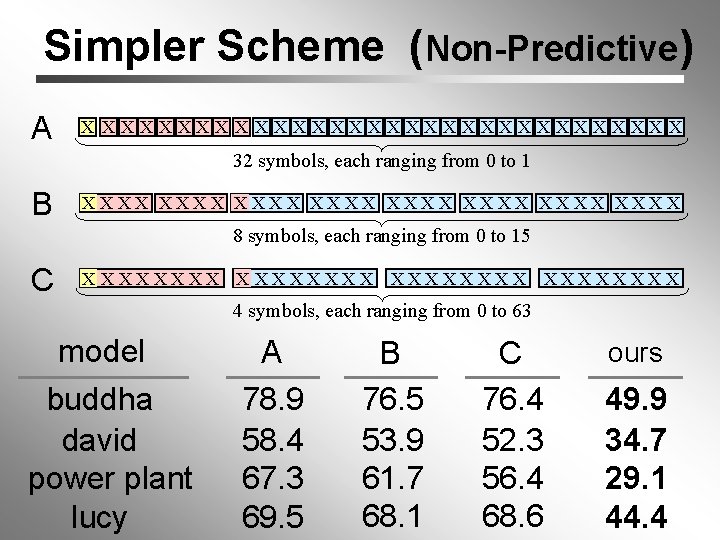
Simpler Scheme (Non-Predictive) A X XXXXXXXXXXXXXXX 32 symbols, each ranging from 0 to 1 B XXXX XXXX 8 symbols, each ranging from 0 to 15 C X XXXXXXXX 4 symbols, each ranging from 0 to 63 model buddha david power plant lucy A 78. 9 58. 4 67. 3 69. 5 B 76. 5 53. 9 61. 7 68. 1 C 76. 4 52. 3 56. 4 68. 6 ours 49. 9 34. 7 29. 1 44. 4

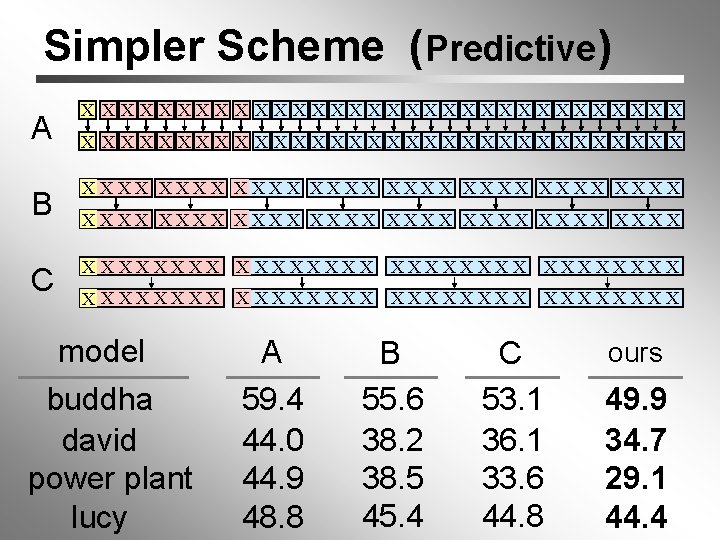
Simpler Scheme (Predictive) A X XXXXXXXXXXXXXXXXXXXXXXX B XXXX XXXX C X XXXXXXXX XXXX XXXX X XXXXXXXX model buddha david power plant lucy A 59. 4 44. 0 44. 9 48. 8 B 55. 6 38. 2 38. 5 45. 4 C 53. 1 36. 1 33. 6 44. 8 ours 49. 9 34. 7 29. 1 44. 4

Talk Overview • Motivation • Geometry Compression • Predictive Schemes • Corrections in Floating-Point • Results • Conclusion

Summary • efficient predictive compression of floating-point in a lossless manner – predict in floating-point – break predicted and actual float into several components – compress differences separately – use exponent to switch contexts • completing, not competing

Current / Future Work • investigate trade-offs – compression versus throughput • optimize implementation – run faster / use less memory • improve scheme for “sparse” data • quantize without bounding box – guarantee precision – learn bounding box

Acknowledgments funding: • LLNL • DOE contract No. W-7405 -Eng-48 models: • Digital Michelangelo Project • UNC Walkthru Group • Newport News Shipbuilding