Lossless Compression I Introduction Compress methods are key

Lossless Compression - I

Introduction § Compress methods are key enabling techniques for multimedia applications. § Raw media takes much storage and bandwidth – A raw video with 30 frame/sec, resolution of 640 x 480, 24 bit color One second of video 30 * 640 * 480 * 3 = 27. 6480 Mbytes One hour video is about 100 Gbytes

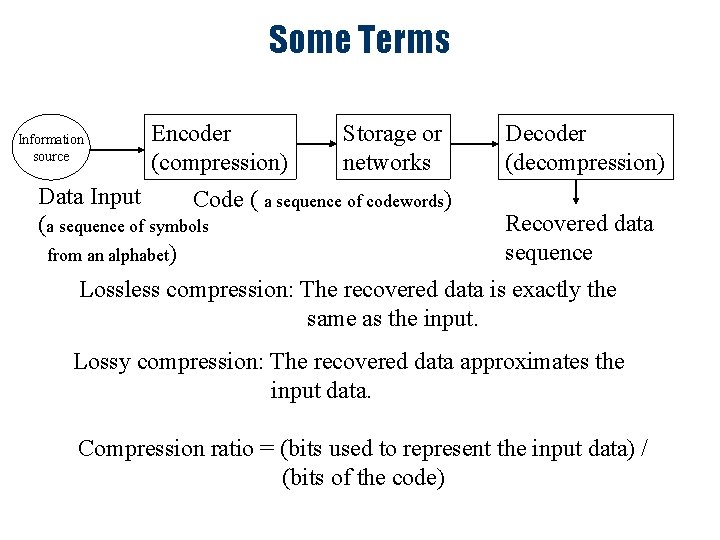
Some Terms Information source Encoder (compression) Storage or networks Decoder (decompression) Data Input Code ( a sequence of codewords) Recovered data (a sequence of symbols sequence from an alphabet) Lossless compression: The recovered data is exactly the same as the input. Lossy compression: The recovered data approximates the input data. Compression ratio = (bits used to represent the input data) / (bits of the code)

Entropy § The number of bits needed to encode a media source is lower-bounded by its “Entropy”. § Self information of an event A is defined as -logb. P(A) where P(A) is the probability of event A. If b equals 2, the unit is “bits”. If b is 10, the unit is “hartleys”

Example § A source outputs two symbols (the alphabet has 2 symbols) 0 or 1. P(0) = 0. 25, P(1) = 0. 75. Information we get when receiving a 0 is log_2 (1/0. 25) = 2 bit ; when receiving a 1 is log_2 (1/0. 75) = 0. 4150 bit.

Properties of Self Information § The letter with smaller probability has high self information. § The information we get when receiving two independent letters are summation of each of the self information. -log 2 P(sa, sb) = -log 2 P(sa)P(sb) = [-log 2 P(sa)] + [- log 2 P(sa)]

Entropy § An source has symbols {s 1, s 2, …, sn}, and the symbols are independent, the average self -information is H= å 1 n P(si)log 2(1/P(si)) bits § H is called the Entropy of the source. § The number of bits per symbol needed to encode a media source is lower-bounded by its “Entropy”.

Entropy (cont) § Example: A source outputs two symbols (the alphabet has 2 letters) 0 or 1. P(0) = 0. 25, P(1) = 0. 75. H = 0. 25 * log_2 (1/0. 25) + 0. 75 * log_2(1/0. 75) = 0. 8113 bits We need at least 0. 8113 bits per symbol in encoding.

The Entropy of an Image § An grayscale image with 256 possible levels. A={0, 1, 2, …, 255}. Assuming the pixels are independent and the grayscales are have equal probabilities, H = 256 * 1/256 *log 2(1/256) = 8 bits § What about an image with only 2 levels 0 and 255? Assuming, P(0) = 0. 5 and P(255) = 0. 5. H = 1 bit

Estimate the Entropy aaabbbbccccdd Assuming the symbols are independent: P(a) = 3/13 P(b) = 4/13 P(c) = 4/13 P(d) = 2/13 H = [-P(a)log_2 P(a)] + [-P(b)log_2 P(b)] + [-P(c)log_2 P(c)] + [-P(d)log_2 P(d)] = 1. 95 bits

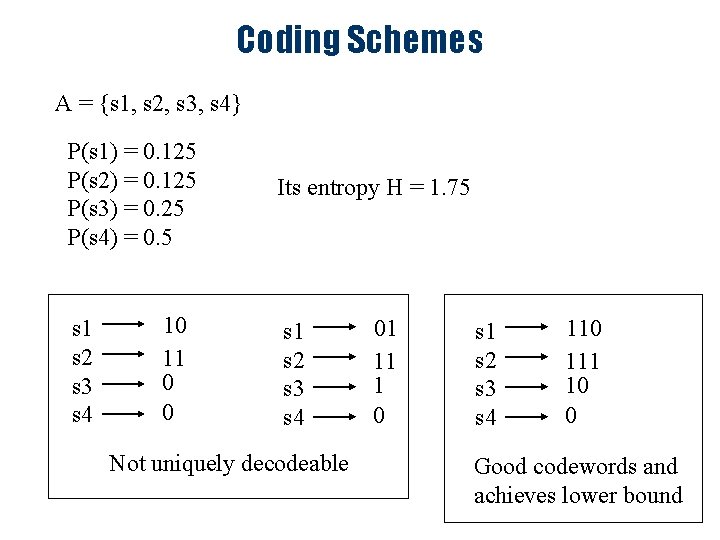
Coding Schemes A = {s 1, s 2, s 3, s 4} P(s 1) = 0. 125 P(s 2) = 0. 125 P(s 3) = 0. 25 P(s 4) = 0. 5 s 1 s 2 s 3 s 4 10 11 0 0 Its entropy H = 1. 75 s 1 s 2 s 3 s 4 Not uniquely decodeable 01 11 1 0 s 1 s 2 s 3 s 4 110 111 10 0 Good codewords and achieves lower bound

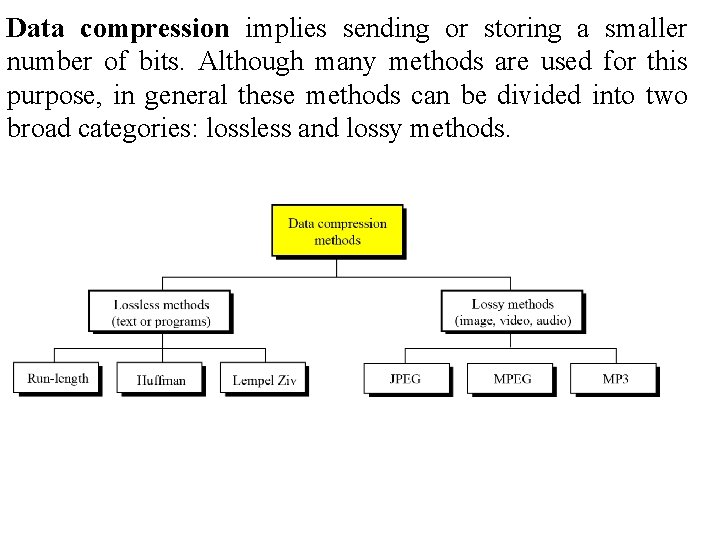
Data compression implies sending or storing a smaller number of bits. Although many methods are used for this purpose, in general these methods can be divided into two broad categories: lossless and lossy methods.

LOSSLESS COMPRESSION In lossless data compression, the integrity of the data is preserved. The original data and the data after compression and decompression are exactly the same because, in these methods, the compression and decompression algorithms are exact inverses of each other: no part of the data is lost in the process. Redundant data is removed in compression and added during decompression. Lossless compression methods are normally used when we cannot afford to lose any data.

Run-length encoding is probably the simplest method of compression. It can be used to compress data made of any combination of symbols. It does not need to know the frequency of occurrence of symbols and can be very efficient if data is represented as 0 s and 1 s. The general idea behind this method is to replace consecutive repeating occurrences of a symbol by one occurrence of the symbol followed by the number of occurrences. The method can be even more efficient if the data uses only two symbols (for example 0 and 1) in its bit pattern and one symbol is more frequent than the other.

CR=Size of original data/size of compressed data CR=36/12