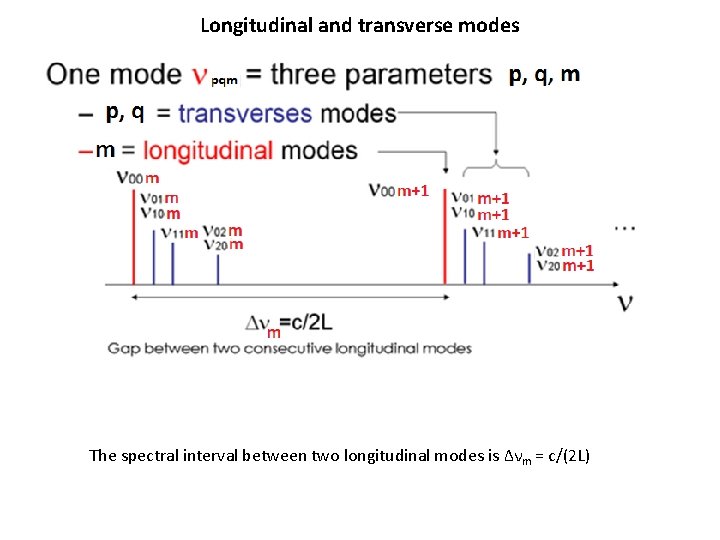
Longitudinal and transverse modes In the case of

Longitudinal and transverse modes In the case of a rectangular parallelepipedic cavity (the sides of the box have height h (x-axis), width w (y-axis), and length L (z-axis), the resonant frequencies are given by : νpqm = (c/2) [(p/h)2 + (q/w)2 +(m/L)2 ] (1/2) where c is the speed of light in vacuum and p, q, m are integers. When L >> h, w and if we take h=w = a to simplify the formula , we obtain : νpqm = (c/2)(m/L) [1 + (p 2+q 2)/a 2 (L 2/m 2)] (1/2) or after a Taylor expansion νpqm = (c/2)(m/L) + (p 2+q 2)/a 2 (c. L/4 m) The frequencies of the longitudinal modes (TEM 00 q) are (see figure 2): (this type of mode are also sometimes called “spectral modes”) νm = (c/2)(m/L).

Longitudinal and transverse modes The spectral interval between two longitudinal modes is Δνm = c/(2 L)

Longitudinal and transverse modes A laser with a single well-defined frequency (corresponding to a given value of m) is a “single-longitudinal- mode laser” : only one longitudinal mode could oscillate, and the laser consequently exhibits a high spectral purity (and then an important coherence length). In a “single-transverse-mode laser”, only the TEM 00 q modes oscillate. The spectral interval between two transverse modes (q and m fixed) is : Δνp = (2 p+1) [c. L / (4 ma 2)]

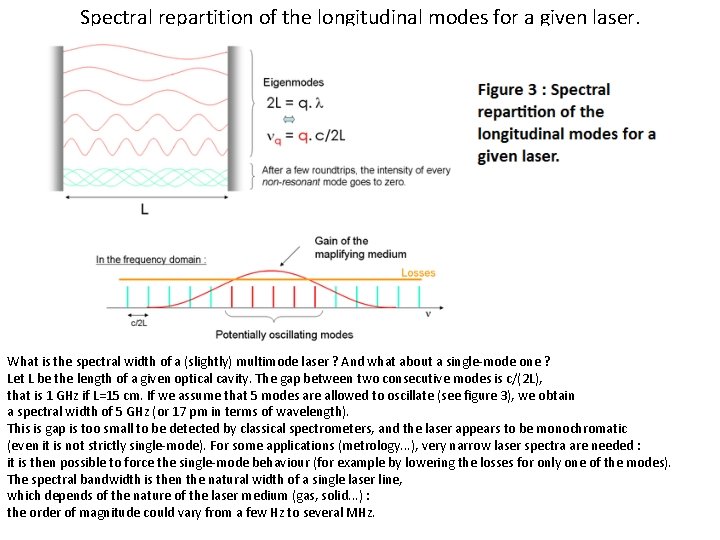
Spectral repartition of the longitudinal modes for a given laser. What is the spectral width of a (slightly) multimode laser ? And what about a single-mode one ? Let L be the length of a given optical cavity. The gap between two consecutive modes is c/(2 L), that is 1 GHz if L=15 cm. If we assume that 5 modes are allowed to oscillate (see figure 3), we obtain a spectral width of 5 GHz (or 17 pm in terms of wavelength). This is gap is too small to be detected by classical spectrometers, and the laser appears to be monochromatic (even it is not strictly single-mode). For some applications (metrology. . . ), very narrow laser spectra are needed : it is then possible to force the single-mode behaviour (for example by lowering the losses for only one of the modes). The spectral bandwidth is then the natural width of a single laser line, which depends of the nature of the laser medium (gas, solid. . . ) : the order of magnitude could vary from a few Hz to several MHz.

Κυλινδρική κοιλότητα Ένταση σε κυλινδρικές συντεταγμένες: ρ = 2 r 2/w 2, w είναι το spot size (FWHM? ) του θεμελιώδους τρόπουTEM 00. Eμφανίζονται τα associated Laguerre polynomials: Τα οποία σχετίζονται με τα Laguerre polynomials: TEMpl όπου p, l δείκτες κόμβων (nodes) ακτινικά και κατά μήκος ημίσειας περιφερείας δηλαδή γωνιακά The overall size of the mode is determined by the Gaussian beam radius w, and this may increase or decrease with the propagation of the beam, however the modes preserve their general shape during propagation. Higher order modes are relatively larger compared to the TEM 00 mode, and thus the fundamental Gaussian mode of a laser may be selected by placing an appropriately sized aperture in the laser cavity.

the first few Laguerre polynomials

Ορθογώνια Παραλληλεπίπεδη Κοιλότητα Ένταση σε καρτεσιανές συντεταγμένες: Όπου w είναι το spot size (FWHM? ) του θεμελιώδους τρόπουTEM 00 και εμφανίζονται τα πολυώνυμα Hermite: Ο τρόπος TEM 00 είναι ο ίδιος με τον TEM 00 της κυλινδρικής κοιλότητας. As before, higher-order modes have a larger spatial extent than the 00 mode. The overall intensity profile of a laser's output may be made up from the superposition of any of the allowed transverse modes of the laser's cavity, though often it is desirable to operate only on the fundamental mode.

the first eleven physicists' Hermite polynomials

Refs and images from http: //www. optiqueingenieur. org/en/courses/OPI_ang_M 01_C 03/co/Contenu_02. html http: //laser. physics. sunysb. edu/~alex/tmodes/webreport. html http: //en. wikipedia. org/wiki/Transverse_mode