Longest Increasing Subsequence Input a sequence of numbers

Longest Increasing Subsequence Input: a sequence of numbers Output: an increasing subsequence Objective: maximize length of the subsequence Example: 2 3 1 7 4 6 9 5

Longest Increasing Subsequence Input: a sequence of numbers Output: an increasing subsequence Objective: maximize length of the subsequence Heart of the solution:

Longest Increasing Subsequence Input: a sequence of numbers Output: an increasing subsequence Objective: maximize length of the subsequence Heart of the solution: S[k] =

Longest Increasing Subsequence Input: a sequence of numbers Output: an increasing subsequence Objective: maximize length of the subsequence Heart of the solution: S[k] = the maximum length of an increasing subsequence of the first k numbers ending with the k-th number

Longest Increasing Subsequence Input: a sequence of numbers a 1, a 2, …, an Output: an increasing subsequence Objective: maximize length of the subsequence Heart of the solution: S[k] = the maximum length of an increasing subsequence of the first k numbers ending with the k-th number S[k] = 1 + maximum S[i] where i < k satisfies ai < ak

Longest Increasing Subsequence LONGEST-INCR-SUBSEQ (a 1, …, an) 1. for k=1 to n do 2. S[k] = 1 3. for j=1 to k-1 do 4. if aj<ak and S[k]<S[j]+1 then 5. 6. 7. S[k] = S[j]+1 end if end for 8. end for 9. return maxk S[k]

Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication

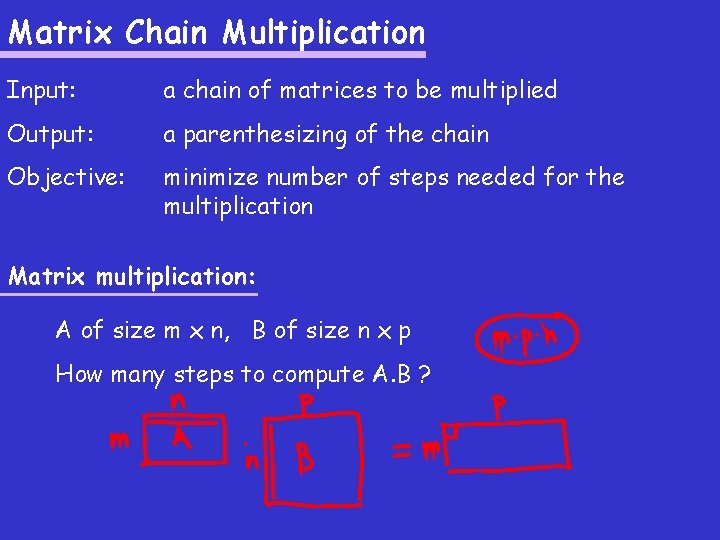
Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication Matrix multiplication: A of size m x n, B of size n x p How many steps to compute A. B ?

Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication Example: 4 2 5 1 2 3

Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication Heart of the solution:

Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication Heart of the solution: S[j, k] =

Matrix Chain Multiplication Input: a chain of matrices to be multiplied Output: a parenthesizing of the chain Objective: minimize number of steps needed for the multiplication Heart of the solution: S[j, k] = the minimum number of steps required to multiply matrices from the j-th to the k-th

Matrix Chain Multiplication MATRIX-CHAIN-MULTIPLICATION (a 1, …, an+1) 1. for j=1 to n do S[j, j] = 0 2. for d=1 to n do 3. for j=1 to n-d do 4. k = j+d 5. S[j, k] = 1 6. for i=j to k-1 7. tmp = S[j, i]+S[i+1, k]+aj. ai+1. ak+1 8. if S[j, k] > tmp then S[j, k] = tmp 9. return S[1, n]