Logistic Regression Rong Jin Logistic Regression Model o

Logistic Regression Rong Jin

Logistic Regression Model o In Gaussian generative model: o Generalize the ratio to a linear model n Parameters: w and c

Logistic Regression Model o In Gaussian generative model: o Generalize the ratio to a linear model n Parameters: w and c

Logistic Regression Model o The log-ratio of positive class to negative class o Results

Logistic Regression Model o The log-ratio of positive class to negative class o Results

Logistic Regression Model o Assume the inputs and outputs are related in the log linear function o Estimate weights: MLE approach

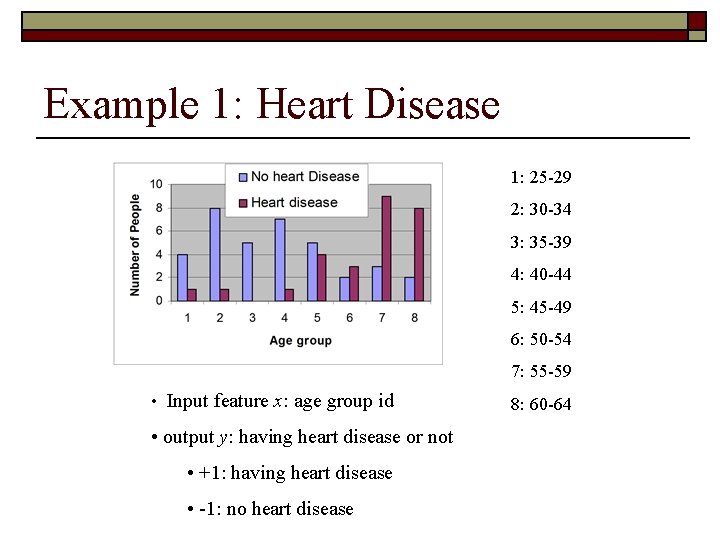
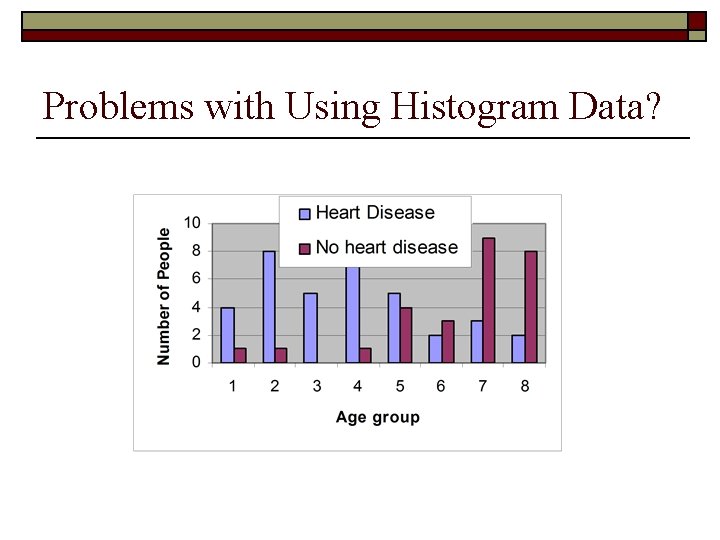
Example 1: Heart Disease 1: 25 -29 2: 30 -34 3: 35 -39 4: 40 -44 5: 45 -49 6: 50 -54 7: 55 -59 • Input feature x: age group id • output y: having heart disease or not • +1: having heart disease • -1: no heart disease 8: 60 -64

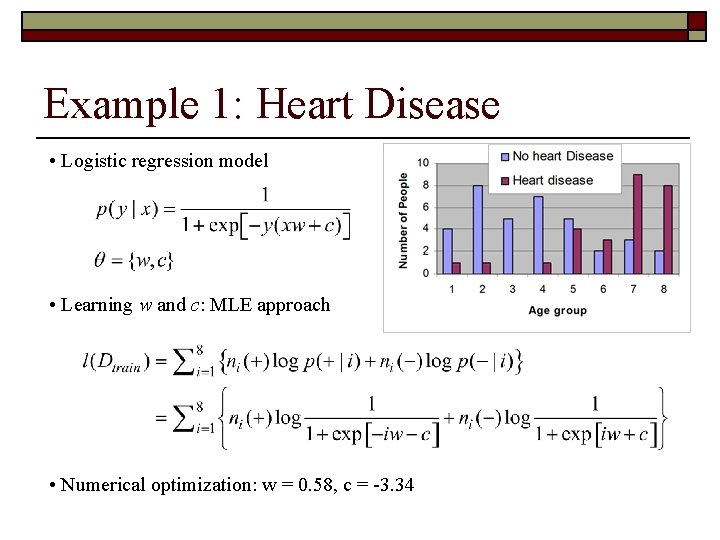
Example 1: Heart Disease • Logistic regression model • Learning w and c: MLE approach • Numerical optimization: w = 0. 58, c = -3. 34

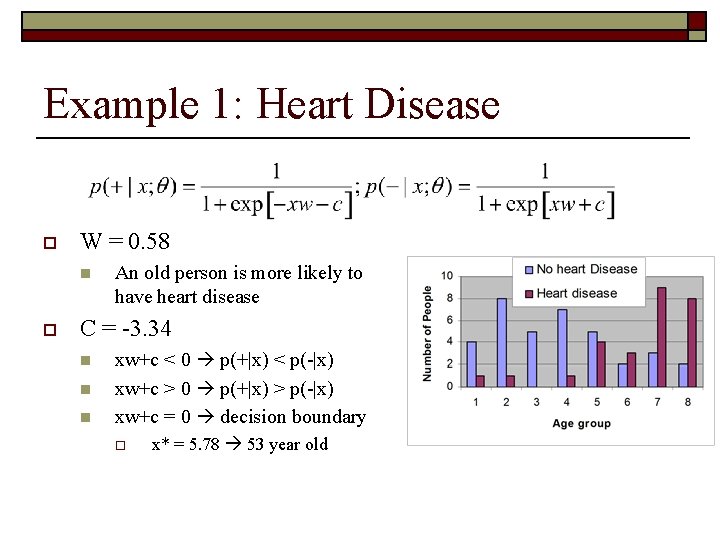
Example 1: Heart Disease o W = 0. 58 n o An old person is more likely to have heart disease C = -3. 34 n n n xw+c < 0 p(+|x) < p(-|x) xw+c > 0 p(+|x) > p(-|x) xw+c = 0 decision boundary o x* = 5. 78 53 year old

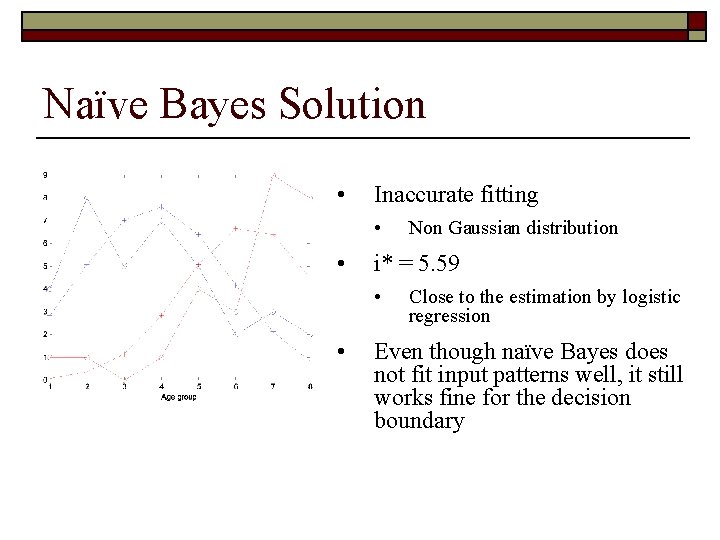
Naïve Bayes Solution • Inaccurate fitting • • i* = 5. 59 • • Non Gaussian distribution Close to the estimation by logistic regression Even though naïve Bayes does not fit input patterns well, it still works fine for the decision boundary

Problems with Using Histogram Data?

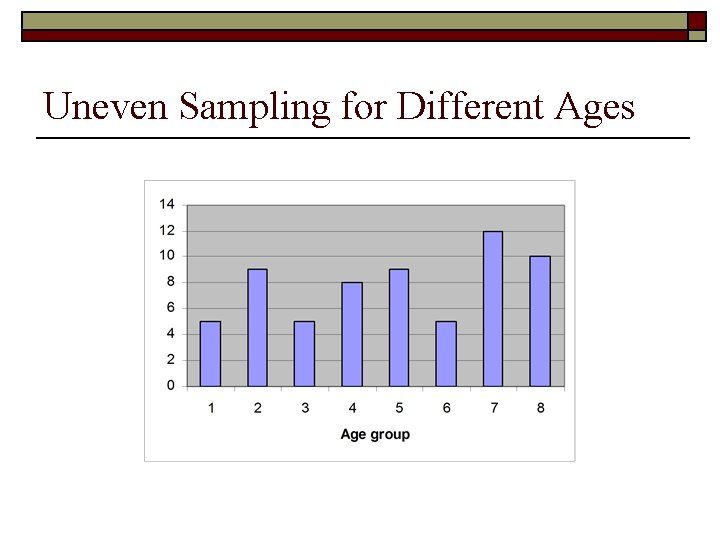
Uneven Sampling for Different Ages

Solution w = 0. 63, c = -3. 56 i* = 5. 65

Solution w = 0. 63, c = -3. 56 i* = 5. 65 < 5. 78

Solution w = 0. 63, c = -3. 56 i* = 5. 65 < 5. 78

Example: Text Classification o o Learn to classify text into predefined categories Input x: a document n n o Output y: if the document is politics or not n o Represented by a vector of words Example: {(president, 10), (bush, 2), (election, 5), …} +1 for political document, -1 for not political document Training data:

Example 2: Text Classification o Logistic regression model n Every term ti is assigned with a weight wi o Learning parameters: MLE approach o Need numerical solutions

Example 2: Text Classification o Logistic regression model n Every term ti is assigned with a weight wi o Learning parameters: MLE approach o Need numerical solutions

Example 2: Text Classification o Weight wi n n o wi > 0: term ti is a positive evidence wi < 0: term ti is a negative evidence wi = 0: term ti is irrelevant to the category of documents The larger the | wi |, the more important ti term is determining whether the document is interesting. Threshold c

Example 2: Text Classification o Weight wi n n o wi > 0: term ti is a positive evidence wi < 0: term ti is a negative evidence wi = 0: term ti is irrelevant to the category of documents The larger the | wi |, the more important ti term is determining whether the document is interesting. Threshold c

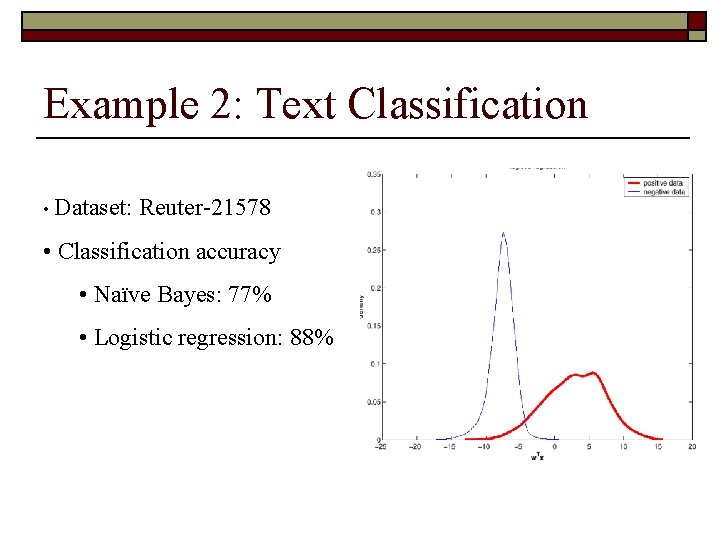
Example 2: Text Classification • Dataset: Reuter-21578 • Classification accuracy • Naïve Bayes: 77% • Logistic regression: 88%

Why Logistic Regression Works better for Text Classification? o Optimal linear decision boundary n Generative model o o o Weight ~ logp(w|+) - logp(w|-) Sub-optimal weights Independence assumption n n Naive Bayes assumes that each word is generated independently Logistic regression is able to take into account of the correlation of words

Discriminative Model o Logistic regression model is a discriminative model n o Models the conditional probability p(y|x), i. e. , the decision boundary Gaussian generative model n Models p(x|y), i. e. , input patterns of different classes

Comparison Generative Model Discriminative Model • Model P(x|y) • Model P(y|x) directly • Model the input patterns • Usually fast converge • Cheap computation • Robust to noise data But • Usually performs worse • Model the decision boundary • Usually good performance But • Slow convergence • Expensive computation • Sensitive to noise data

Comparison Generative Model Discriminative Model • Model P(x|y) • Model P(y|x) directly • Model the input patterns • Usually fast converge • Cheap computation • Robust to noise data But • Usually performs worse • Model the decision boundary • Usually good performance But • Slow convergence • Expensive computation • Sensitive to noise data

A Few Words about Optimization o o Convex objective function Solution could be non-unique

Problems with Logistic Regression? How about words that only appears in one class?

Overfitting Problem with Logistic Regression o Consider word t that only appears in one document d, and d is a positive document. Let w be its associated weight o Consider the derivative of l(Dtrain) with respect to w will be infinite !

Overfitting Problem with Logistic Regression o Consider word t that only appears in one document d, and d is a positive document. Let w be its associated weight o Consider the derivative of l(Dtrain) with respect to w will be infinite !

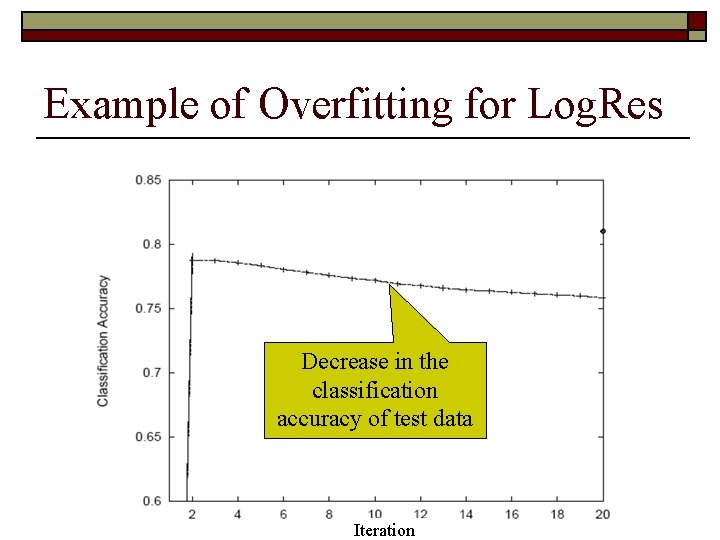
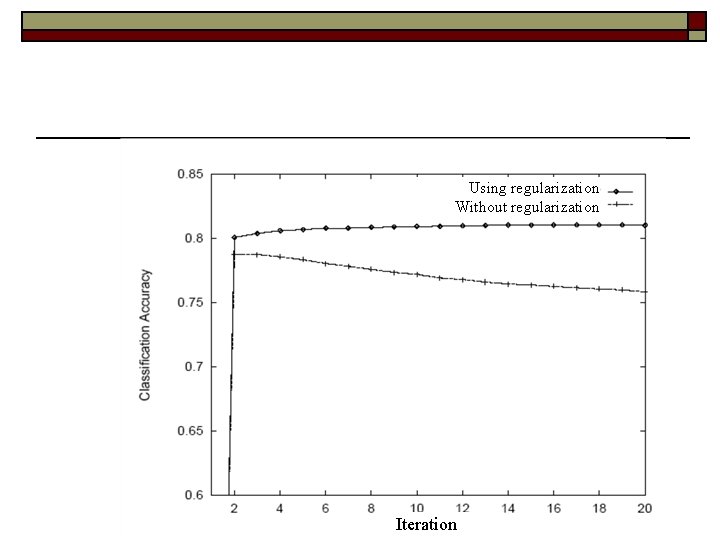
Example of Overfitting for Log. Res Decrease in the classification accuracy of test data Iteration

Solution: Regularization o Regularized log-likelihood o s||w||2 is called the regularizer n n Favors small weights Prevents weights from becoming too large

The Rare Word Problem o Consider word t that only appears in one document d, and d is a positive document. Let w be its associated weight

The Rare Word Problem o Consider the derivative of l(Dtrain) with respect to w o When s is small, the derivative is still positive But, it becomes negative when w is large o

The Rare Word Problem o Consider the derivative of l(Dtrain) with respect to w o When w is small, the derivative is still positive But, it becomes negative when w is large o

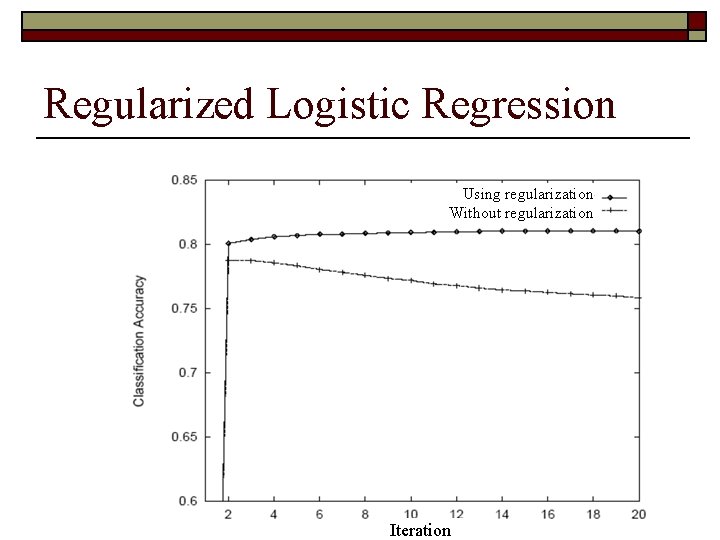
Regularized Logistic Regression Using regularization Without regularization Iteration

Interpretation of Regularizer o Many interpretation of regularizer n n n Bayesian stat. : model prior Statistical learning: minimize the generalized error Robust optimization: min-max solution

Regularizer: Robust Optimization o o assume each data point is unknown-but-bounded in a sphere of radius s and center xi find the classifier w that is able to classify the unknown-butbounded data point with high classification confidence

Sparse Solution o o What does the solution of regularized logistic regression look like ? A sparse solution n Most weights are small and close to zero

Sparse Solution o o What does the solution of regularized logistic regression look like ? A sparse solution n Most weights are small and close to zero

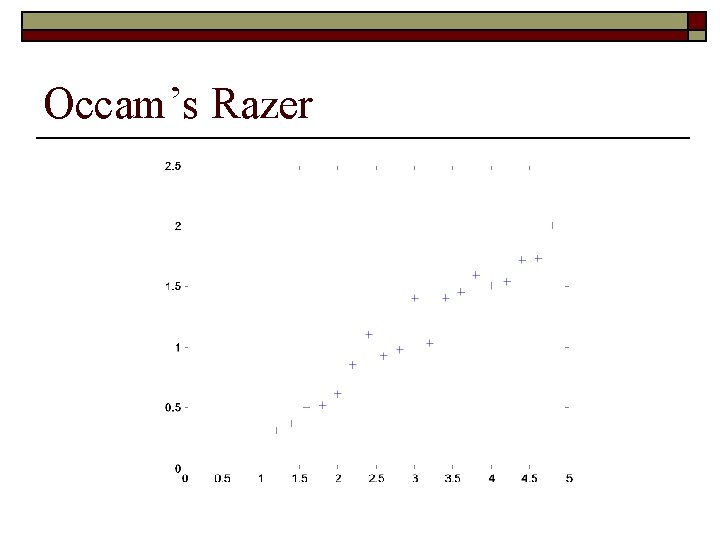
Why do We Need Sparse Solution? o Two types of solutions 1. 2. o Many non-zero weights but many of them are small Only a small number of non-zero weights, and many of them are large Occam’s Razor: the simpler the better n n n A simpler model that fits data unlikely to be coincidence A complicated model that fit data might be coincidence Smaller number of non-zero weights less amount of evidence to consider simpler model case 2 is preferred

Occam’s Razer

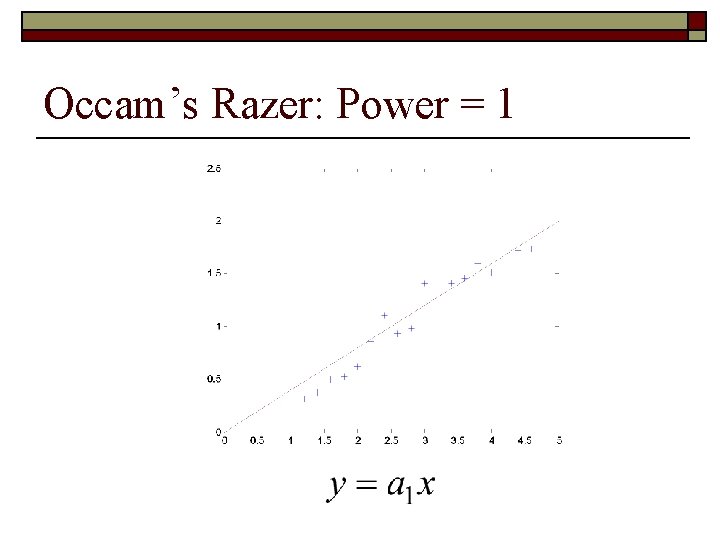
Occam’s Razer: Power = 1

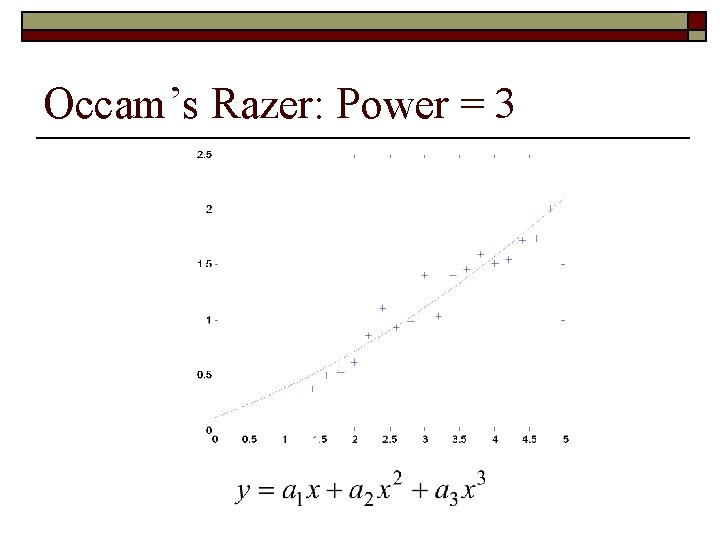
Occam’s Razer: Power = 3

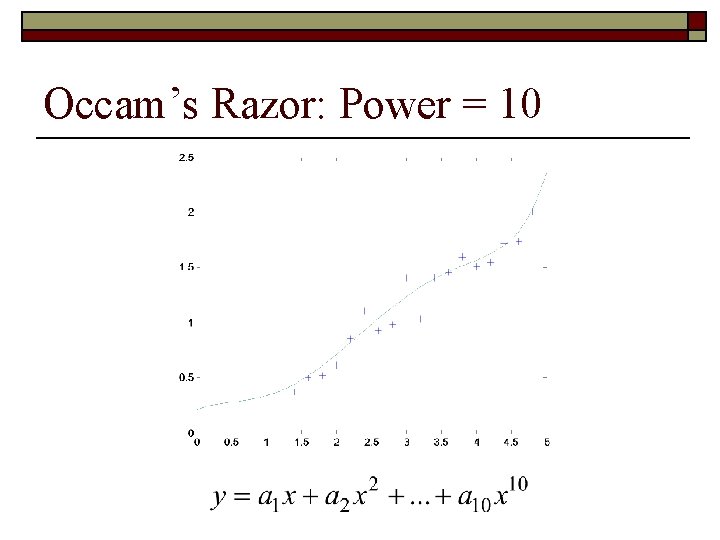
Occam’s Razor: Power = 10

Finding Optimal Solutions o o Concave objective function No local maximum n Many standard optimization algorithms work

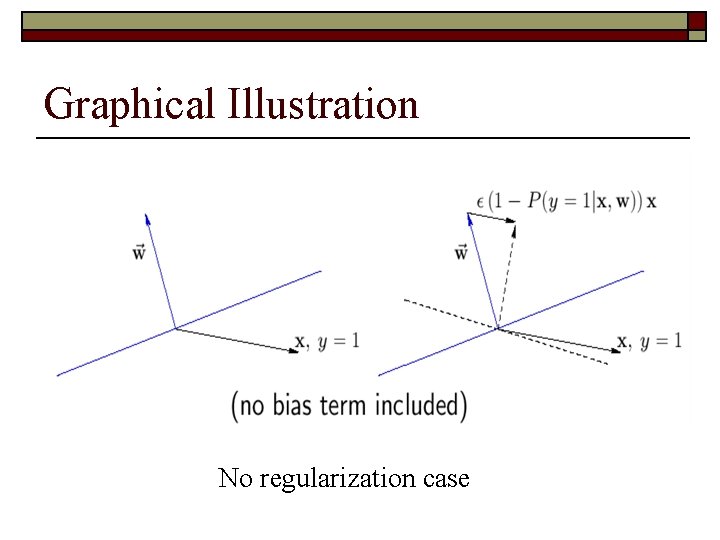
Gradient Ascent o o Maximize the log-likelihood by iteratively adjusting the parameters in small increments In each iteration, we adjust w in the direction that increases the log-likelihood (toward the gradient) Predication Errors Preventing weights from being too large

Graphical Illustration No regularization case

Gradient Ascent o o Maximize the log-likelihood by iteratively adjusting the parameters in small increments In each iteration, we adjust w in the direction that increases the log-likelihood (toward the gradient)

Using regularization Without regularization Iteration

When should Stop? o The gradient ascent learning method converges when there is no incentive to move the parameters in any particular direction: