Logistic Regression Rong Jin Logistic Regression Generative models

Logistic Regression Rong Jin

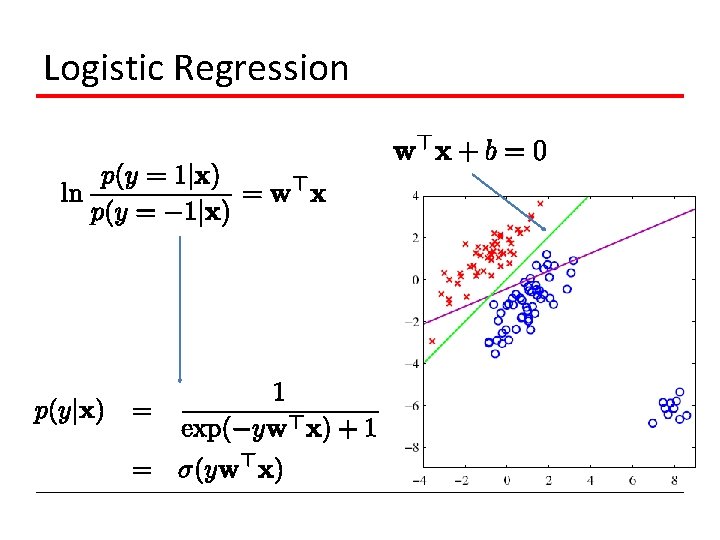
Logistic Regression • Generative models often lead to linear decision boundary • Linear discriminatory model • Directly model the linear decision boundary • w is the parameter to be decided

Logistic Regression

Logistic Regression Learn parameter w by Maximum Likelihood Estimation (MLE) • Given training data

Logistic Regression • Convex objective function, global optimal Classification error • Gradient descent

Logistic Regression • Convex objective function, global optimal Classification error • Gradient descent

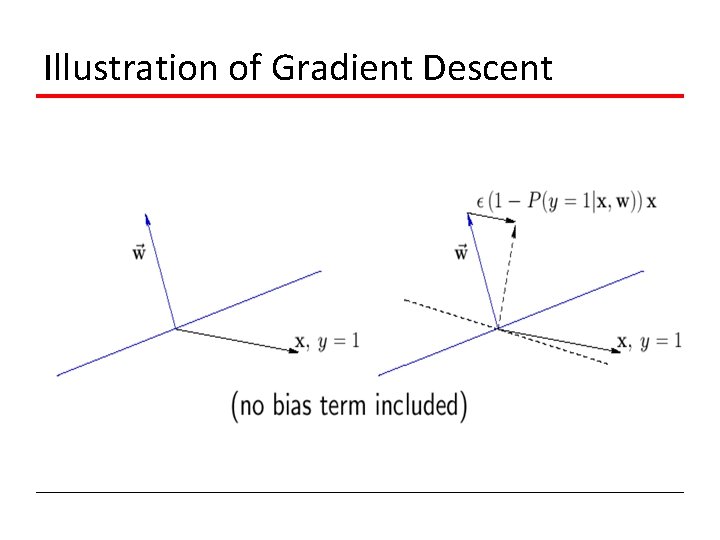
Illustration of Gradient Descent

How to Decide the Step Size ? • Back track line search

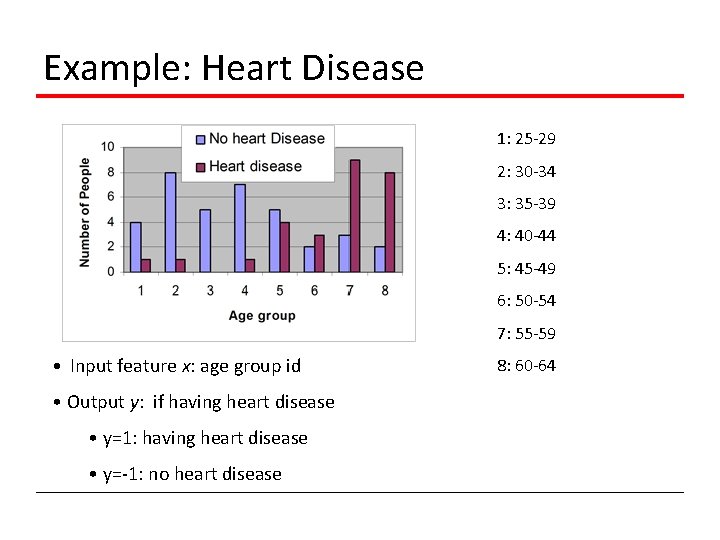
Example: Heart Disease 1: 25 -29 2: 30 -34 3: 35 -39 4: 40 -44 5: 45 -49 6: 50 -54 7: 55 -59 • Input feature x: age group id • Output y: if having heart disease • y=1: having heart disease • y=-1: no heart disease 8: 60 -64

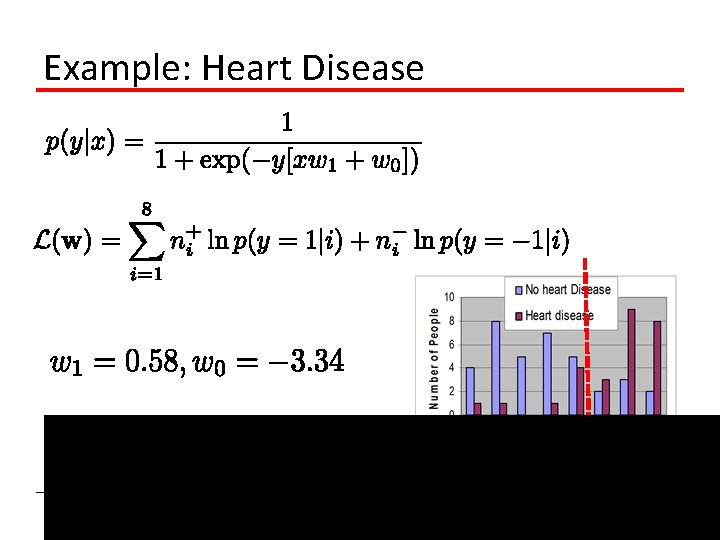
Example: Heart Disease

Example: Text Categorization Learn to classify text into two categories • Input d: a document, represented by a word histogram • Output y= 1: +1 for political document, -1 for nonpolitical document

Example: Text Categorization • Training data

Example 2: Text Classification • Dataset: Reuter-21578 • Classification accuracy • Naïve Bayes: 77% • Logistic regression: 88%

Logistic Regression vs. Naïve Bayes • Both are linear decision boundaries • Naïve Bayes: • Logistic regression: learn weights by MLE • Both can be viewed as modeling p(d|y) • Naïve Bayes: independence assumption • Logistic regression: assume an exponential family distribution for p(d|y) (a broad assumption)

Logistic Regression vs. Naïve Bayes

Discriminative vs. Generative Discriminative Models Model P(y|x) Pros • Usually good performance Cons • Slow convergence • Expensive computation • Sensitive to noise data Generative Models Model P(x|y) Pros • Usually fast converge • Cheap computation • Robust to noise data Cons • Usually performs worse

Overfitting Problem Consider text categorization • What is the weight for a word j appears in only one training document dk?

Overfitting Problem

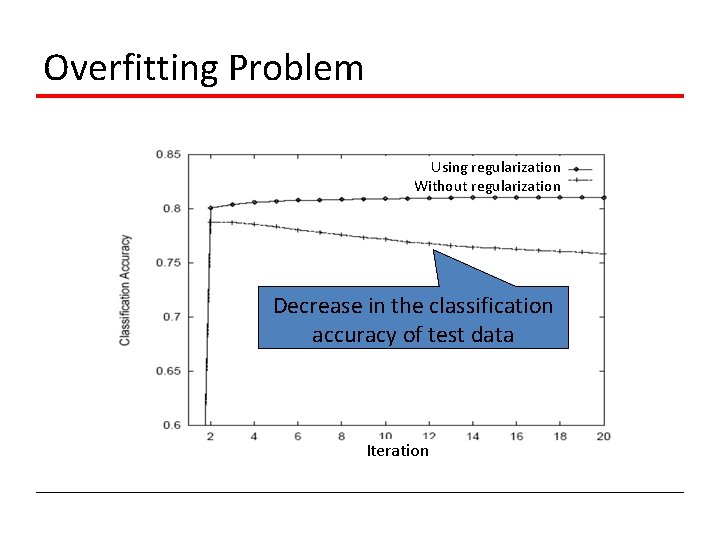
Overfitting Problem Using regularization Without regularization Decrease in the classification accuracy of test data Iteration

Solution: Regularization Regularized log-likelihood The effects of regularizer • Favor small weights • Guarantee bounded norm of w • Guarantee the unique solution

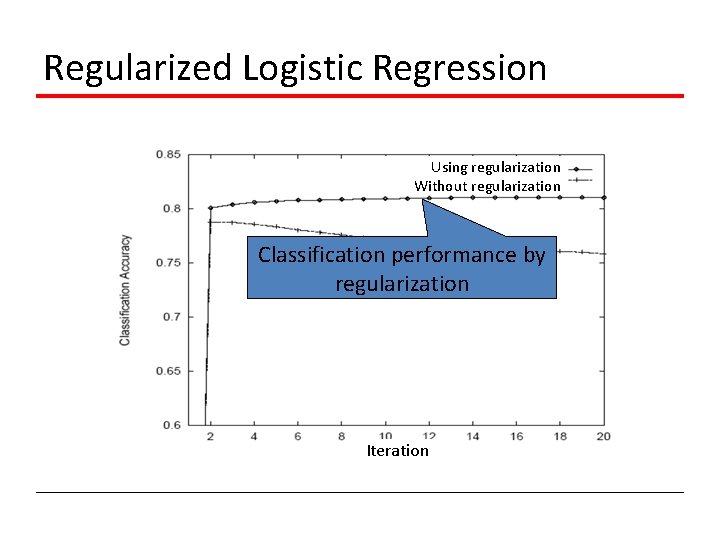
Regularized Logistic Regression Using regularization Without regularization Classification performance by regularization Iteration

Regularization as Robust Optimization • Assume each data point is unknown but bounded in a sphere of radius r and center xi

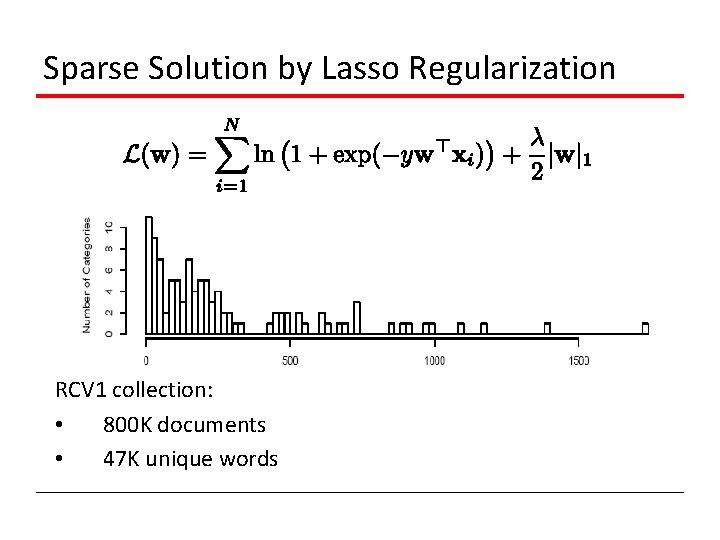
Sparse Solution by Lasso Regularization RCV 1 collection: • 800 K documents • 47 K unique words

Sparse Solution by Lasso Regularization How to solve the optimization problem? • Subgradient descent • Minimax

Bayesian Treatment • Compute the posterior distribution of w • Laplacian approximation

Bayesian Treatment • Laplacian approximation

Multi-class Logistic Regression • How to extend logistic regression model to multi-classification ?

Conditional Exponential Model • Let classes be Normalization factor (partition function) • Need to learn

Conditional Exponential Model • Learn weights ws by maximum likelihood estimation • Any problem ?

Modified Conditional Exponential Model