Logistic Regression 1 Sociology 8811 Lecture 4 Copyright

Logistic Regression 1 Sociology 8811 Lecture 4 Copyright © 2007 by Evan Schofer Do not copy or distribute without permission

Announcements • Lab Assignment #1 due on Monday • Get in the habit of bringing a calculator to class • It isn’t absolutely necessary, but it will help with interpreting logistic regression coefficients…

Reasons for advanced methods • OLS regression is great… why do we need to learn more? • Answer: You need a “toolbox” of methods to deal with common situations • 1. Different types of variables require different tools • Crosstabs = useful for examining the relationship among 2 categorical variables • Correlation and OLS regression = good for identifying linear relationships among interval variables • We’ll learn appropriate techniques for other combinations of variables – Ex: Logistic regression for dichotomous dependent variables.

Reasons for advanced methods • 2. Some types of data create problems for standard tools like OLS regression – Ex: Often we like to observe cases repeatedly over time… but this can violate OLS assumptions – You need “time-series” regression models • 3. Sometimes you want to accomplish tasks beyond simply looking for relationships among variables • Ex: Network analysis; latent class models; geometric data analysis – Not covered in this class…

Upcoming Topics • • • Logistic Regression Count Models Event History Analysis Multilevel models (e. g. , HLM) Structural equation models with latent variables (SEM)

Review: Types of Variables • Continuous variable = can be measured with infinite precision • Age: we may round off, but great precision is possible • Discrete variable = can only take on a specific set of values • Typically: Positive integers or a small set of categories • Ex: # children living in a household; Race; gender • Note: Dichotomous = discrete with 2 categories.

Review: Types of Variables • And, don’t forget about measurement scales: • Nominal: Categories that can’t be ordered • Note: Also called “categorical” variables • Ex: Religion; race; geographic state of residence • Ordinal: Orderable categories • Ex: Social class; College “rankings”; Most attitudinal measures (Do you approve of… on a 1 -5 scale) • Interval/Continuous: Ordered, with consistent differences across units • Ex: Age; Cholesterol level; Income (in dollars).

Review: OLS Regression • Question: What kinds of variables can be analyzed with OLS regression? – Basic correlation and regression was designed for 2 interval/ratio variables • Does fat consumption correlate with cholesterol level? – Also: It is easy to incorporate nominal/categorical independent variables • Strategy: Use dummy variables in regression • Ex: Is gender associated with cholesterol level? – Also: OLS is “robust” and works reasonably well with many ordinal measures (ideally 5+ categories) • Ex: Are environmental attitudes associated with approval of the president?

Example 1: OLS Regression • Example: Study time and student achievement. – X variable: Average # hours spent studying per day – Y variable: Score on reading test Case X Y 1 2. 6 28 2 1. 4 13 3 . 65 19 4 4. 1 31 5 . 25 6 1. 9 16 8 Y axis 30 20 10 0 X axis 0 1 2 3 4

Example 2: Dichotomous Variable • Ex: Did students pass the test (score > 18)? • Does OLS regression make sense here? Case X Y 1 2. 6 1 2 1. 4 0 3 . 65 1 4 4. 1 1 5 . 25 0 6 1. 9 0 Y axis Pass (1) Fail (0) X axis 0 1 2 3 4

OLS & Dichotomous Variables • Problem: OLS regression wasn’t really designed for dichotomous dependent variables! • Two possible outcomes (typically labeled 0 & 1) • What kinds of problems come up? – Linearity assumption doesn’t hold up – Error distribution is not normal – The model offers nonsensical predicted values • Instead of predicting pass (1) or fail (0), the regression line might predict -. 5.

The Linear Probability Model (LPM) • Solution #1: Use OLS regression anyway! • Dependent variable = the probability that a case scores 1 (as opposed to 0) • In previous example, 1 = passed test; 0 = failed. – We’ll assume that the probability changes as a linear function of independent variables: • Note: This assumption may not be appropriate

Linear Probability Model (LPM) • The LPM may yield reasonable results • Often good enough to get a “crude look” at your data • Results tend to be better if data is well behaved – Ex: If there are decent numbers of cases in each category of the dependent variable. • Interpretation: – Coefficients (b) reflect the increase in probability of Y=1 for each unit change in X – Constant (a) reflects the base probability of Y=1 if all X variables are zero – Significance tests are done; but may not be trustworthy due to OLS assumption violations.

LPM Example: Own a gun? • Stata OLS output: . regress gun male educ income south liberal Source | SS df MS -------+---------------Model | 18. 3727851 5 3. 67455703 Residual | 173. 628391 844. 205720843 -------+---------------Total | 192. 001176 849. 226149796 Number of obs F( 5, 844) Prob > F R-squared Adj R-squared Root MSE = = = 850 17. 86 0. 0000 0. 0957 0. 0903. 45356 ---------------------------------------gun | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------+--------------------------------male |. 1637871. 0314914 5. 20 0. 000. 1019765. 2255978 educ | -. 0153661. 00525 -2. 93 0. 004 -. 0256706 -. 0050616 income |. 0379628. 0071879 5. 28 0. 000. 0238546. 0520711 south |. 1539077. 0420305 3. 66 0. 000. 0714111. 2364043 liberal | -. 0313841. 011572 -2. 71 0. 007 -. 0540974 -. 0086708 _cons |. 13901. 1027844 1. 35 0. 177 -. 0627331. 3407531 --------------------------------------- Interpretation: Each additional year of education decreases probability of gun ownership by. 015. What about other vars?

LPM Example: Own a gun? • OLS results can yield predicted probabilities • Just plug in values of constant, X’s into linear equation • Ex: A conservative, poor, southern male: ---------------------------------------gun | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------+--------------------------------male |. 1637871. 0314914 5. 20 0. 000. 1019765. 2255978 educ | -. 0153661. 00525 -2. 93 0. 004 -. 0256706 -. 0050616 income |. 0379628. 0071879 5. 28 0. 000. 0238546. 0520711 south |. 1539077. 0420305 3. 66 0. 000. 0714111. 2364043 liberal | -. 0313841. 011572 -2. 71 0. 007 -. 0540974 -. 0086708 _cons |. 13901. 1027844 1. 35 0. 177 -. 0627331. 3407531 ---------------------------------------

LPM Example: Own a gun? • Predicted probability for a female Ph. D student • Highly educated northern liberal female ---------------------------------------gun | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------+--------------------------------male |. 1637871. 0314914 5. 20 0. 000. 1019765. 2255978 educ | -. 0153661. 00525 -2. 93 0. 004 -. 0256706 -. 0050616 income |. 0379628. 0071879 5. 28 0. 000. 0238546. 0520711 south |. 1539077. 0420305 3. 66 0. 000. 0714111. 2364043 liberal | -. 0313841. 011572 -2. 71 0. 007 -. 0540974 -. 0086708 _cons |. 13901. 1027844 1. 35 0. 177 -. 0627331. 3407531 ---------------------------------------

LPM: Weaknesses • Model yields nonsensical predicted values • Probabilities should always fall between 0 and 1. • Assumptions of OLS regression are violated • Linearity • Homoskedasticity (Equal error variance across values of X): error = low near 0, 1 & high at other values. • Normality of error distribution – Coefficients (b) are not biased; but not “best” (i. e. , lowest possible sampling variance) – Variances & Standard errors will be inaccurate • Hypothesis tests (t-tests, f-tests) can’t be trusted

Logistic Regression • Better Alternative: Logistic Regression • Also called “Logit” • A non-linear form of regression that works well for dichotomous dependent variables • Other non-linear formulations also work (e. g. , probit) • Based on “odds” rather than probability • Rather than model P(Y=1), we model “log odds” of Y=1 • “Logit” refers to the natural log of an odds… – Logistic regression is regression for a logit • Rather than a simple variable “Y” (OLS) • Or a probability (the Linear Probability Model).

Probability & Odds • Probability of event A defined as p(A): • Example: Coin Flip… probability of “heads” • 1 outcome is “heads”, 2 total possible outcomes • P(“heads”) = 1 / 2 =. 5 • Odds of A = Number of outcomes that are A, divided by number of outcomes that are not A • Odds of “heads” = 1 / 1 = 1. 0 • Also equivalent to: probability of event over probability of it not happening: p/(1 -p) = (. 5 / 1 -. 5) = 1. 0

Logistic Regression • We can convert a probability to odds: • “Logit” = natural log (ln) of an odds • Natural log means base “e”, not base 10 – We can model a logit as a function of independent variables: • Just as we model Y or a probability (the LPM)

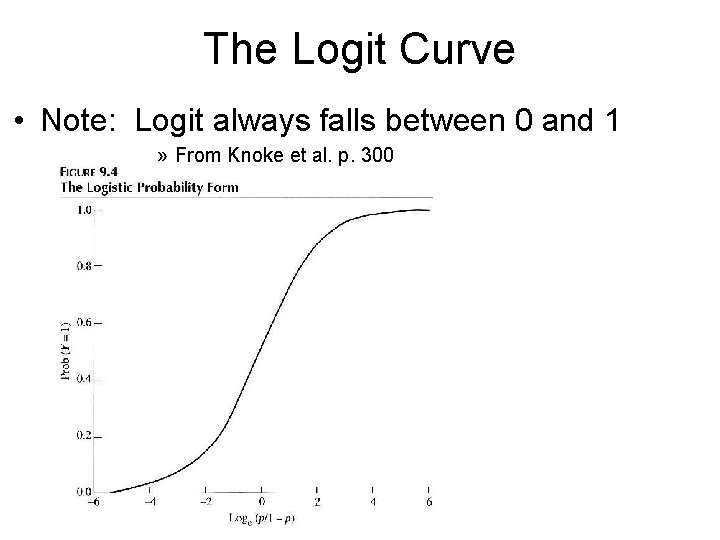
The Logit Curve • Note: Logit always falls between 0 and 1 » From Knoke et al. p. 300

Logistic Regression • Note: We can solve for “p” and reformulate the model: • Why model this rather than a probability? – Because it is a useful non-linear transformation • It always generates Ps between 0 and 1, regardless of the values of X variables • Note: probit transformation has similar effect.

Logistic Regression: Estimation • Estimation: We can model the logit • Recall: “Hat” = estimate… • Solution requires Maximum Likelihood Estimation (MLE) • In OLS there was an algebraic solution • Here, we allow the computer to “search” for the best values of coefficients (“a” and “b”s) to fit observed data.

Logistic Regression: Estimation • Properties of Maximum Likelihood Estimation – See Long & Freese 2003: 69, Long 1997: 54 for a summary • “Consistent, efficient and asymptotically normal as N approaches infinity. ” Large N = better! – Rules of thumb regarding sample size • N > 500 = fine; N < 100 can be worrisome – Results aren’t necessarily wrong if N<100; – But it is a possibility; and hard to know when problems crop up • Plus ~10 cases per independent variable • Eliason (1993) suggests minimum N~60 for up to 5 IVs – Higher N is needed if data are problematic due to: • Multicollinearity • Limited variation in dependent variable.

Logistic Regression • Benefits of Logistic regression: • You can now effectively model probability as a function of X variables • You don’t have to worry about violations of OLS assumptions • Predictions fall between 0 and 1 • Downsides – You lose the “simple” interpretation of linear coefficients • In a linear model, effect of each unit change in X on Y is consistent • In a non-linear model, the effect isn’t consistent… • Also, you can’t compute some stats (e. g. , R-square).

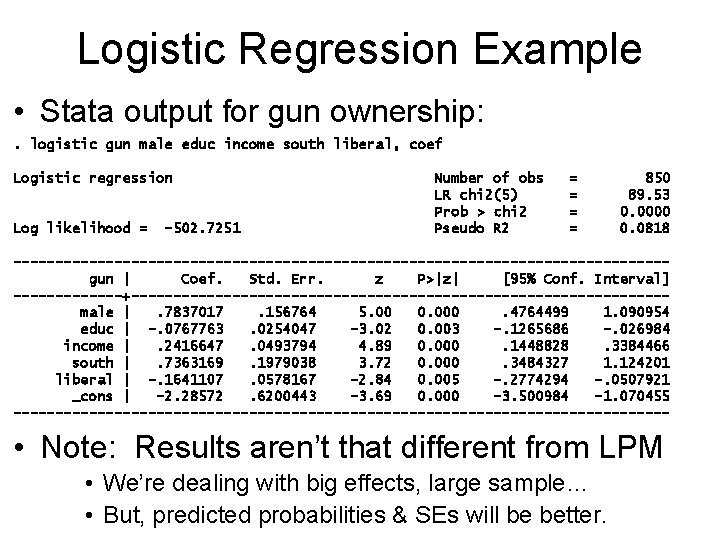
Logistic Regression Example • Stata output for gun ownership: . logistic gun male educ income south liberal, coef Logistic regression Log likelihood = -502. 7251 Number of obs LR chi 2(5) Prob > chi 2 Pseudo R 2 = = 850 89. 53 0. 0000 0. 0818 ---------------------------------------gun | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------+--------------------------------male |. 7837017. 156764 5. 00 0. 000. 4764499 1. 090954 educ | -. 0767763. 0254047 -3. 02 0. 003 -. 1265686 -. 026984 income |. 2416647. 0493794 4. 89 0. 000. 1448828. 3384466 south |. 7363169. 1979038 3. 72 0. 000. 3484327 1. 124201 liberal | -. 1641107. 0578167 -2. 84 0. 005 -. 2774294 -. 0507921 _cons | -2. 28572. 6200443 -3. 69 0. 000 -3. 500984 -1. 070455 --------------------------------------- • Note: Results aren’t that different from LPM • We’re dealing with big effects, large sample… • But, predicted probabilities & SEs will be better.

Interpreting Coefficients • Raw coefficients (bs) show effect of 1 -unit change in X on the log odds of Y=1 – Positive coefficients make “Y=1” more likely • Negative coefficients mean “less likely” – But, effects are not linear • Effect of unit change on p(Y=1) isn’t same for all values of X! – Rather, Xs have a linear effect on the “log odds” • But, it is hard to think in units of “log odds”, so we need to do further calculations • NOTE: log-odds interpretation doesn’t work on Probit!

Interpreting Coefficients • Best way to interpret logit coefficients is to exponentiate them • This converts from “log odds” to simple “odds” • Exponentiation = opposite of natural log – On calculator use “ex” or “inverse ln” function – Exponentiated coefficients are called odds ratios • An odds ratio of 3. 0 indicates odds are 3 times higher for each unit change in X – Or, you can say the odds increase “by a factor of 3”. • An odds ratio of. 5 indicates odds decrease by ½ for each unit change in X. – Odds ratios < 1 indicate negative effects.

Interpreting Coefficients • Example: Do you drink coffee? • Y=1 indicates coffee drinkers; Y=0 indicates no coffee • Key independent variable: Year in grad program – Observed “raw” coefficient: b = 0. 67 • A positive effect… each year increases log odds by. 67 • But how big is it really? – Exponentiation: e. 67= 1. 95 • Odds increase multiplicatively by 1. 95 • If a person’s initial odds were 2. 0 (2: 1), an extra year of school would result in: 2. 0*1. 95 = 3. 90 • The odds nearly DOUBLE for each unit change in X – Net of other variables in the model…

Interpreting Coefficients • Exponentiated coefficients (“odds ratios”) operate multiplicatively • Effect on odds is found by multiplying coefficients – eb of 1. 0 means that a variable has no effect • Multiplying anything by 1. 0 results in same value – eb > 1. 0 means that the variable has a positive effect on the odds of “Y=1” • eb < 1. 0 means that the variable has a negative effect • Hint: Papers may present results as “raw” coefficients or odds ratios • It is important to be aware of what you’re looking at • If all coeffs are positive, you’re looking at odds ratios!

Interpreting Coefficients • To further aid interpretation, we can: convert exponentiated coefficients to % change in odds – Calculate: (exponentiated coef - 1)*100% • Ex: (e. 67 – 1) * 100% = (1. 95 – 1) * 100% = 95% • Interpretation: Every unit change in X (year of school) increases the odds of coffee drinking by 95% • What about a 2 -point change in X? • Is it 2 * 95%? No!!! You must multiply odds ratios: • (1. 95 * 1. 95 – 1) * 100% = (3. 80 – 1) * 100 = +280% – 3 -point change = (1. 95 * 1. 95 – 1) * 100% • N-point change = (ORn – 1) * 100%

Interpreting Coefficients • What is the effect of a 1 -unit decrease in X? • No, you can’t flip sign… it isn’t -95% – You must invert odds ratios to see opposite effect • Additional year in school = (1. 95 – 1) * 100% = +95% • One year less: (1/1. 95 – 1)*100 =(. 512 -1)*100= -48. 7% • What is the effect of two variables together? • To combine odds ratios you must multiply – Ex: Have a mean advisor; b=. 1. 2; OR = e 1. 2 = 3. 32 • Effect of 1 additional year AND mean advisor: • (1. 95 * 3. 32 – 1)*100 = (6. 47 – 1) * 100% = 547% increase in odds of coffee drinking…

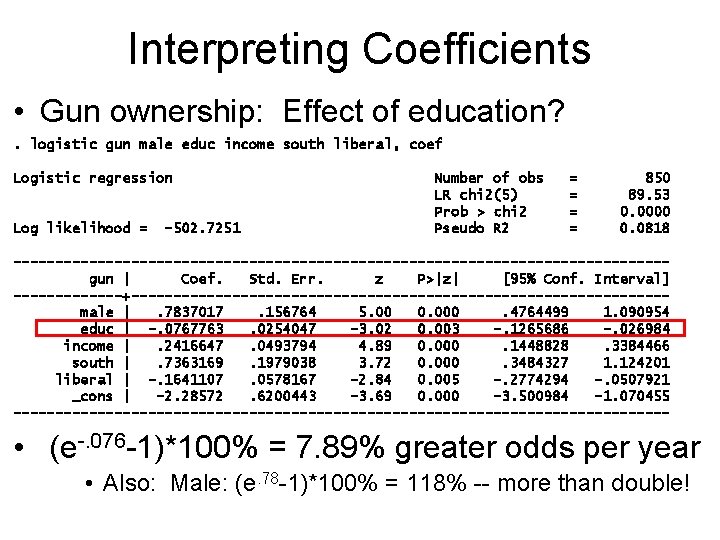
Interpreting Coefficients • Gun ownership: Effect of education? . logistic gun male educ income south liberal, coef Logistic regression Log likelihood = -502. 7251 Number of obs LR chi 2(5) Prob > chi 2 Pseudo R 2 = = 850 89. 53 0. 0000 0. 0818 ---------------------------------------gun | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------+--------------------------------male |. 7837017. 156764 5. 00 0. 000. 4764499 1. 090954 educ | -. 0767763. 0254047 -3. 02 0. 003 -. 1265686 -. 026984 income |. 2416647. 0493794 4. 89 0. 000. 1448828. 3384466 south |. 7363169. 1979038 3. 72 0. 000. 3484327 1. 124201 liberal | -. 1641107. 0578167 -2. 84 0. 005 -. 2774294 -. 0507921 _cons | -2. 28572. 6200443 -3. 69 0. 000 -3. 500984 -1. 070455 --------------------------------------- • (e-. 076 -1)*100% = 7. 89% greater odds per year • Also: Male: (e. 78 -1)*100% = 118% -- more than double!

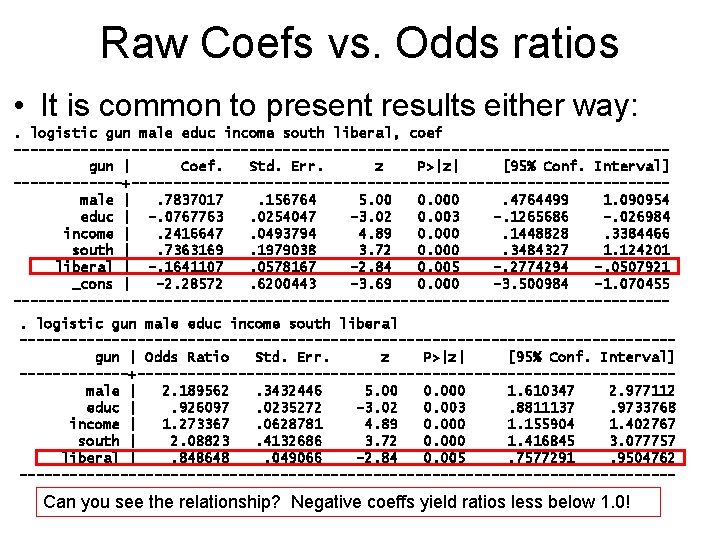
Raw Coefs vs. Odds ratios • It is common to present results either way: . logistic gun male educ income south liberal, coef ---------------------------------------gun | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------+--------------------------------male |. 7837017. 156764 5. 00 0. 000. 4764499 1. 090954 educ | -. 0767763. 0254047 -3. 02 0. 003 -. 1265686 -. 026984 income |. 2416647. 0493794 4. 89 0. 000. 1448828. 3384466 south |. 7363169. 1979038 3. 72 0. 000. 3484327 1. 124201 liberal | -. 1641107. 0578167 -2. 84 0. 005 -. 2774294 -. 0507921 _cons | -2. 28572. 6200443 -3. 69 0. 000 -3. 500984 -1. 070455 ---------------------------------------. logistic gun male educ income south liberal ---------------------------------------gun | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------+--------------------------------male | 2. 189562. 3432446 5. 00 0. 000 1. 610347 2. 977112 educ |. 926097. 0235272 -3. 02 0. 003. 8811137. 9733768 income | 1. 273367. 0628781 4. 89 0. 000 1. 155904 1. 402767 south | 2. 08823. 4132686 3. 72 0. 000 1. 416845 3. 077757 liberal |. 848648. 049066 -2. 84 0. 005. 7577291. 9504762 --------------------------------------- Can you see the relationship? Negative coeffs yield ratios less below 1. 0!

Predicted Probabilities • To determine predicted probabilities, first compute the predicted Logit value: • Then, plug logit values back into P formula:

LPM Example: Own a gun? • Predicted probability for a female Ph. D student • Highly educated northern liberal female ---------------------------------------gun | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------+--------------------------------male |. 7837017. 156764 5. 00 0. 000. 4764499 1. 090954 educ | -. 0767763. 0254047 -3. 02 0. 003 -. 1265686 -. 026984 income |. 2416647. 0493794 4. 89 0. 000. 1448828. 3384466 south |. 7363169. 1979038 3. 72 0. 000. 3484327 1. 124201 liberal | -. 1641107. 0578167 -2. 84 0. 005 -. 2774294 -. 0507921 _cons | -2. 28572. 6200443 -3. 69 0. 000 -3. 500984 -1. 070455 ---------------------------------------

Predicted Probabilities • Predicted probabilities are a great way to make findings accessible to a reader – Often people make bar graphs of probabilities – 1. Show predicted probabilities for real cases • Ex: probability of civil war for Ghana vs. Sweden – 2. Show probabilities for “hypothetical” cases that exemplify key contrasts in your data • Ex: Guns: Southern male vs. female Ph. D student – 3. Show a change in critical independent variable would affect predicted probability • Ex: Guns: What would happen to southern male who went and got a Ph. D?

Hypothesis tests • Testing hypotheses using logistic regression • H 0: There is no effect of year in grad program on coffee drinking • H 1: Year in grad school is associated with coffee – Or, one-tail test: Year in school increases probability of coffee – MLE estimation yields standard errors… like OLS – Test statistic: 2 options; both yield same results • t = b/SE… just like OLS regression • Wald test (Chi-square, 1 df); essentially the square of t – Reject H 0 if Wald or t > critical value • Or if p-value less than alpha (usually. 05).