LOGIKA PROPOSISI Logika Pernyataan Pengertian Proposisi adalah pernyataanpernyataan

LOGIKA PROPOSISI (Logika Pernyataan)

Pengertian • Proposisi adalah pernyataan-pernyataan yang berbeda pada suatu argument, dan pernyataan tersebut mempunyai property nilai, yang hanya benar saja atau salah saja, serta tidak ada nilai lain yang dimungkinkan. Pernyataan apa saja yang mempunyai nilai BENAR atau SALAH disebut proposisi

• Membicarakan tentang pernyatan tunggal dan kata hubungnya sehinga didapat pernyataan majemuk. • Kalimat deklaratif, tabel nilai

Tabel Kebenaran • Logika adalah ilmu tentang penalaran • Penalaran Berarti mencari bukti validitas dari suatu argument, mencari konsistensi dari pernyataan-pernyataan, dan membahas materi tentang kebenaran dan ketidakbenaran. • Logika hanya berhubungan dengan bentuk-bentuk (form) logika dari argument-argument, serta penarikan kesimpulan tentang validitas dari argument tersebut. • Logika tidak mempermasalahkan arti sebenarnya dari pernyataan tersebut, ataupun isi (content) dari pernyataan

• Penekanan logika pada penarikan kesimpulan tentang validitas suatu argument untuk mendapatkan kebenaran yang bersifat abstrak, yang dibangun dengan memakai kaidah-kaidah dasar logika tentang kebenaran dan ketidakbenaran yang menggunakan perangkai logika, yaitu: o Dan (and) o Atau (or) o Tidak (not) o Jika…maka… (if…then…) o …jika dan hanya jika… (…if and only if…)

Perangkai Logika atau Operator • Setiap perangkai pada logika memiliki nilai kebenarannya masing sesuai jenis perangkai logika yang digunakan. • Untuk mengetahui nilai kebenarannya, digunakan aturan dengan memakai table kebenaran. • Perangkai logika atau operator dalam bentuk symbol dipergunakan untuk membuat bentuk-bentuk logika atau ekspresi logika. • Di sini hanya digunakan konstanta proposional T untuk True dan F untuk False, bukan B dan atau S.

Perangkai-perangkai logika yang digunakan adalah:

Konjungsi [Ʌ] • Konjungsi (conjunction) adalah kata lain dari perangka “dan (and)” • Tabel Kebenaran Konjungsi: A F F T B F T F AɅB F F F T T T

Disjungsi [V] • Tanda v digunakan sama dengan perangkai “atau (or)”. • Tabel kebenaran disjungsi: A F F T B F T F AVB F T T T

Negasi [¬] • Negasi (negation) digunakan untuk menggantikan perangkai “tidak(not)” • Tabel Kebenaran negasi: A F T ¬A T F

Implikasi [→] • Implikasi (implication) menggantikan perangkai “jika…maka… (if…then…) • Tabel kebearan implikasi: A F F T B F T F A→B T T F T T T

Ekuivalensi [↔] • Ekuivalensi (equivalence) menggantikan perangkai “…jika dan hanya jika… (…. if and only if…. )”. • Tabel kebenaran ekuivalensi: A F F T B F T F A↔B T F F T T T

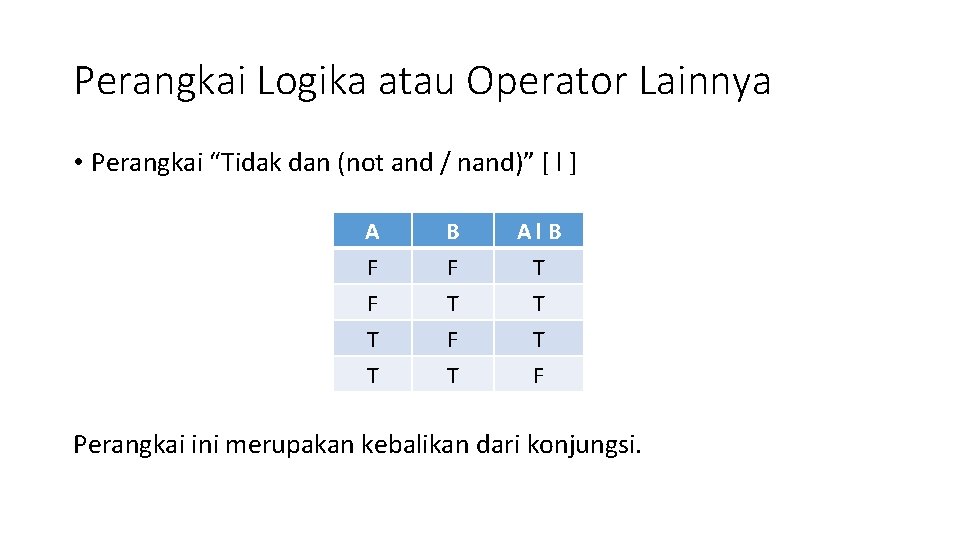
Perangkai Logika atau Operator Lainnya • Perangkai “Tidak dan (not and / nand)” [ l ] A F F T B F T F Al. B T T T F Perangkai ini merupakan kebalikan dari konjungsi.

• Perangkai “tidak atau (not or / nor)” [↓] A F F T B F T F A↓B T F F T T F • Perangkai ini merupakan kebalikan dari disjungsi.

• Perangkai XOR (exlusive or) • Perangkai ini merupakan kebalikan dari ekuivalensi.