LOGIKA PERNYATAAN DAN BUKAN PERNYATAAN LOGICAL PROPOSITION AND

LOGIKA PERNYATAAN DAN BUKAN PERNYATAAN

LOGICAL PROPOSITION AND NOT PROPOSITION

LOGIKA Standar Kompetensi Menerapkan logika matematika dalam pemecahan masalah yang berkaitan dengan pernyataan majemuk dan pernyataan berkuantor Kompetensi Dasar 1. Mendiskripsikan pernyataan dan bukan pernyataan (kalimat terbuka). 2. Mendiskripsikan ingkaran, konjungsi, disjungsi, implikasi, biimplikasi, dan ingkarannya. 3. Mendiskripsikan invers, konvers, dan Kontraposisi. 4. Menerapkan modus ponens, modus tollens dan prinsip silogisme dalam menarik kesimpulan. Hal. : LOGIKA Adaptif

LOGICAL Competence Standard Applying mathematic logical in solving a problem related to compound statement and quantor statemen. Basic Competence 1. Describing statement and not statement (open sentence). 2. Describing negation, conjunction, disjunction, implication, biimplication, and its negation. 3. Describing inverse, converse, and contraposition. 4. Applying Ponens modus, Tollens modus, and Syllogism principle in drawing conclusion. Hal. : LOGIKA Adaptif

LOGIKA Indikator: 1. Membedakan pernyataan dan kalimat terbuka. 2. Menentukan nilai kebenaran suatu pernyataan. 3. Mendeskripsikan ingkaran, konjungsi, disjungsi, implikasi, biimplikasi dan ingkarannya. 4. Mendiskripsikan invers, konvers, dan kontraposisi. Hal. : LOGIKA Adaptif

LOGICAL Indicator: 1. Differentiate between statement and open sentence. 2. Define the truth value of a statement. 3. Describing negation, conjunction, disjunction, implication, biimplication and its negation. 4. Describing inverse, converse, and contraposition. Hal. : LOGIKA Adaptif

PERNYATAAN DAN BUKAN PERNYATAAN A. PERNYATAAN Pernyataan adalah kalimat yang hanya bernilai benar saja atau salah saja, tidak bisa sekaligus benar dan salah Suatu pernyataan biasanya dilambangkan dengan huruf kecil seperti : a, b, c , dll. Contoh: a : 2 adalah bilangan genap (bernilai benar) b : 4 habis dibagi 3 (bernilai salah) Pernyataan yang benar dikatakan mempunyai nilai kebenaran B (benar), sedangkan pernyataan yang salah dikatakan mempunyai nilai kebenaran S (salah). Kata nilai kebenaan dilambangkan dengan (tau). Contoh: a: 8 adalah bilangan genap, merupakan pernyataan yang benar, (a)=B p : 5 lebih kecil dari 4, merupakan pernyataan yang salah, (p)=S Hal. : LOGIKA Adaptif

Proposition is a sentence which can explain something true or false. A proposition is usually symbolized by small letter, such as a, b, c, etc. Examples: a : 2 is an even number (true) b : 4 can be divided by 3 (false) The truth proposition has truth value T (true), while the false proposition has the truth value F (false). The truth value of proposition can be denoted as (tau) Examples: a : 8 is an even number, it is a truth proposition, (a) = T p : 5 is less than 4, it is a false proposition, (p) = F Hal. : LOGIKA Adaptif

KALIMAT TERBUKA B. KALIMAT TERBUKA Kalimat terbuka adalah yang memuat peubah/variable, sehingga belum dapat ditentukan nilai kebenarannya (benar/salah) Contoh: 2. itu adalah benda cair A. NEGASI Jika p merupakan sebuah pernyataan, maka ingkaran atau negasi dari p ditulis dengan lambang ~p. Contoh: p: 7 adalah bilangan prima , maka ~p: 7 bukan bilangan prima q : 3+2 sama dengan 6 , maka ~q: 3+2 tidak sama dengan 6 Tabel kebenaran Hal. : p ~p B S S B LOGIKA Adaptif

Open Sentences (Not Proposition) Open sentences containing variables, so can not be determined the truth value yet. Examples : 1. 2. It is liquid A. NEGATION If p is a proposition, then the negation of p is written by ~p and it is read as not p or p is not true. Examples : p : 7 is prime number, then ~p: 7 is not prime number q : 3+2 is equal to 6, then ~q: 3+2 is not equal to 6 The truth table p T F Hal. : F T LOGIKA Adaptif

DISJUNGSI B. DISJUNGSI Disjungsi adalah gabungan dari dua pernyataan yang dirangkai dengan menggunakan kata hubung atau. Disjungsi pernyataan p dan pernyataan q, ditulis dengan lambang: Tabel kebenaran disjungsi adalah sebagai berikut: P q B B S S B S Hal. : B B B S “ Ingatlah “ “ Siswa harus membawa pencil dan bolpoint “ LOGIKA Adaptif

Disjunction is two proposition which uses a connective “OR” Proposition disjunction of p and q, denoted as read as p or q The truth table of disjunction is as follows: Hal. : p q T T S S T F Sentences to remember : T T T F “ students, you have to bring pencil or pen ” LOGIKA Adaptif

KONJUNGSI C. KONJUNGSI Konjungsi adalah pernyataan yang dibentuk dari dua pernyataan yang dirangkai dengan kata hubung atau. Konjungsi pernyataan p dan pernyataan q, ditulis dengan lambang: Dibaca p dan q Tabel kebenaran P q B B S S B S Hal. : “ Ingatlah “ “ Siswa harus membawa pencil dan bolpoint “ B S S S LOGIKA Adaptif

Conjunction is a kind of compound proposition, which uses a connective “AND” Conjunction of proposition p and q denoted as The truth table of p q B B S S B S Hal. : B S S S and read p dan q Sentences to remember : “ students, you have to bring book and pen ” LOGIKA Adaptif

IMPLIKASI D. IMPLIKASI Implikasi adalah pernyataan majemuk yang dibentuk dari dua pernyataan p dan pernyataan q dalam bentuk jika p maka q Implikasi jika p maka q ditulis dengan lambang: Dibaca jika p maka q atau p hanya jika q q jika p p syarat cukup bagi q q syarat perlu bagi p Tabel kebenaran implikasi adalah sebagai berikut: P q B B S S B S Hal. : Kalimat untuk mengingat : “ jika kamu lulus ujian maka kamu saya beri hadiah “ B S B B LOGIKA Adaptif

Implication is a compound proposition which is formed from two proposition of p and q denoted as if p then q The implication if p then q is denoted as The truth table of implication is as follows: Read if p then q or p only if q q if p p is sufficient condition for q q is necessary condition for p Hal. : LOGIKA p q T T F F T F T T Adaptif

BIIMPLIKASI E. BIIMPLIKASI Biimplikasi dari pernyataan-pernyataan p dan q dapat dituliskan sebagai berikut: dibaca : p jika dan hanya jika q Jika p maka q dan jika q maka p p syarat perlu dan cukup bagi q q syarat perlu dan cukup bagi p Tabel kebenaran Hal. : P q B B S S B S B S S B LOGIKA Adaptif

Biimplication from propositions p and q can be denoted as and read as • • p if and only if q If p then q and if q then p p is necessary condition and enough for q q is necessary condition and enough for p The truth table : Hal. : p q T T F F T F LOGIKA T F F T Adaptif

PERNYATAAN MAJEMUK Pernyataan majemuk adalah pernyataan yang dibentuk dari beberapa pernyataan tunggal (componen) yang dirangkai dengan menggunakan kata hubung logika. Contoh pernyataan majemuk: 1. 2. Contoh: Tentukan nilai kebenaran dari Untuk menentukan nilai kebenaran, biasanya menggunakan tabel kebenaran P q B B S S B S B B B S B Jadi nilai kebenaran dari Atau ditulis: Hal. : B B B S adalah B, B, B, S BBBS LOGIKA Adaptif

Compound Proposition Compound proposition is a proposition formed from a few single sentences. They are AND (Λ), OR (V), IF …, THEN …( =>), AND IF ONLY IF … ( ) The examples compound proposition 1. 2. Examples : Determine the truth value of To determine the truth value, usually using the truth table : p q ~q (pv~q)=>p T T F T T T F F T T F Hal. : So, the truth value of (pv~q) => p is T, T, T, F or denoted as : LOGIKA TTTF Adaptif

TAUTOLOGI Tautologi adalah sebuah pernyataan majemuk yang selalu benar untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya. Contoh: Tunjukkan bahwa pernyataan majemuk Tabel p B B S S Jadi pernyataan q (pvq) B S B B B S adalah sebuah tautologi B B merupakan tautologi KONTRADIKSI Kontradiksi adalah sebuah pernyataan majemuk yang selalu salah untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya. Hal. : LOGIKA Adaptif

Tautology is a compound proposition which always true for all possible valuation of proposition component Example : adalah sebuah tautologi Show that the compound proposition Table p q (pvq) T T F F T F T T T F So the proposition p => (pvq) T T is Tautology Kontradiction is a compound proposition which always false for all possible valuation of proposition component Hal. : LOGIKA Adaptif

PERNYATAAN MAJEMUK DUA BUAH PERNYATAAN MAJEMUK YANG EKUIVALEN Dua buah penyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk itu memiliki nilai kebenaran yang sama untuk semua kemungkinan nilai kebenaran pernyataan komponen-komponennya Lambang dari dua buah pernyataan majemuk yang equivalen adalah Ekuivalen Hal. : LOGIKA Adaptif

PERNYATAAN MAJEMUK Lanjutan p : Mama mengantar adik , q : Saya belajar (p V q) : Mama mengantar adik atau saya belajar ~(p V q) : (~p ~q) =Mama tidak mengantar adik dan saya tidak belajar p : Saya naik kelas , q : Saya dapat hadiah p q : Jika Saya naik kelas maka Saya dapat hadiah ~(p q) =(p ~q) : Saya naik kelas dan Saya tidak dapat hadiah Saya naik kelas tetapi Saya tidak dapat hadiah Hal. : LOGIKA Adaptif

The Equivalence of Two Compound Proposition The two compound proposition is called equivalent if those two compound sentences have the same truth value for all possible valuation of proposition component The equivalence of two compound proposition is denoted by p ≡ q Equivalent Hal. : LOGIKA Adaptif

The Equivalence of Two Compound Proposition Next p : Mother takes my sister , q : I am studying (p V q) : Mother takes my sister or, I am studying ~(p V q) : (~p ~q) = Mother doesn’t take my sister and I am not studying p : I pass to the next grade , q : I get present p q : If I pass the next grade then I get present ~(p q) =(p ~q) : I pass to the next grade and I don’t get present I pass to the next grade but I don’t get present Hal. : LOGIKA Adaptif
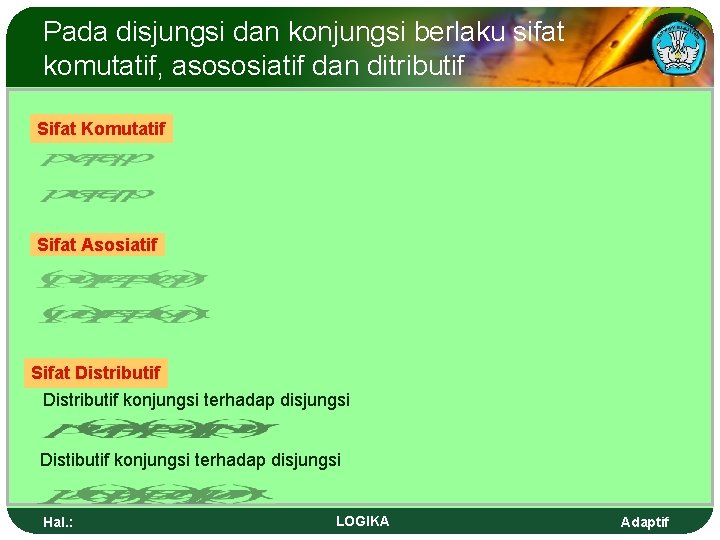
Pada disjungsi dan konjungsi berlaku sifat komutatif, asososiatif dan ditributif Sifat Komutatif Sifat Asosiatif Sifat Distributif konjungsi terhadap disjungsi Distibutif konjungsi terhadap disjungsi Hal. : LOGIKA Adaptif

The Equivalence of Two Compound Proposition In disjunction and conjuction, they have commulative law, associative law, and distributive law. Commutative Law Associative Law Distributive conjunction to disjunction Hal. : LOGIKA Adaptif

. HUBUNGAN KONVERS, INVERS, DAN KONTRAPOSISI DENGAN IMPLIKASI Jika kita mempunyai sebuah implikasi , maka kita bisa membuat beberapa buah implikasi yang lain, yaitu , disebut konvers dari implikasi , disebut invers dari implikasi , disebut kontraposisi dari implikasi p q B B B ~q p q S S B B B S B B S S S B B B B Hal. : ~p ~q ~p q p ~p ~q ≡ Implikasi ekuivalen dengan kontraposisinya ≡ Konvers ekuivalen dengan invers LOGIKA Adaptif

The Correlation Between Converse, Inverse, Controposition and Implication If we have an implication , then we can mate another implication, they are : , is called converse from implication , is called inverse from implication , is called contraposition from implication Hal. : p q ~p ~q p q ~q ~p q p ~p ~q B B S S B B S B B S S B B B ≡ Implication equivalent with its contraposition ≡ Converse equivalent with its inverse LOGIKA Adaptif

KUANTOR UNIVERSAL Semua siswa Kelas X SMA Satu pandai. Kata semua atau setiap merupakan kuantor universal (umum) Lambang dari kuator universal adalah: dibaca, untuk semua x berlakulah p(x) atau dibaca, untuk semua x anggota S berlakulah p(x) Hal. : LOGIKA Adaptif

Universal Quantor All students of grade X of senior high school 1 are clever The words “All” every are universal equator (general) The symbol of universal equator are : Read as for all x, we have p(x) or Read as, for all x is S member, we have p(x) Hal. : LOGIKA Adaptif

KUANTOR EKSISTENSIAL Lanjutan KUANTOR EKSISTENSIAL Beberapa siswa kelas X SMA Satu pandai. Kata beberapa atau ada merupakan kuantor eksistensial (khusus) Misalkan: U=himpunan semua siswa SMA di Jakarta A=himpunan semua siswa SMA Satu B=himpunan semua siswa kelas X SMA satu yang pandai Pernyataan “Beberapa siswa kelas X SMA Satu pandai”, dapat ditulis dengan lambang berikut: dibaca: Beberapa siswa SMA Satu pandai, atau Sekurang-kurangnya ada seorang siswa kelas X SMA Satu yang pandai. Hal. : LOGIKA Adaptif

Universal Quantor Existential Quantor A few students of grade X of senior high school are clever. The word “a few” or “there are/there is” are exsistential quantor (specific) Examples: U = a set of all students of senior high school in Jakarta A = a set of all students of senior high school 1 B = a set of all grade X students of senior high school 1 who are clever The proposition of “a few of grade X students of senior high school ! are clever”, can be denoted by Read : a few students of senior high school 1 are clever, OR at least a student of grade X of senior high school 1 is clever Hal. : LOGIKA Adaptif

INGKARAN PERNYATAAN BERKUANTOR Contoh: p : Semua siswa Satu rajin belajar ~p : Ada siswa Satu yang tidak rajin belajar q : Ada siswa Satu yang rumahnya di Kelapa Gading ~q : Semua siswa Satu rumahnya tidak di Kelapa Gading r : Jika semua siswa kelas satu naik kelas maka Saya senang ~r : Semua siswa kelas satu naik kelas dan Saya tidak senang ~r : Semua siswa kelas satu naik kelas tetapi Saya tidak senang Hal. : LOGIKA Adaptif

NEGATION OF QUANTORED STATEMENT Negation of quantored statement Example: p : All the first grade students are diligent ~p : There is one students who is not diligent q : There is one students whose house is in Kelapa Gading ~q : All of the first grade students’ house are not in Kelapa Gading r : If all the first grade students pass to the next grade, then I am happy ~r : All the first grade students pass to the next grade and I am not happy ~r : All the first grade students pass to the next grade but I am not happy Hal. : LOGIKA Adaptif

Drawing Conclusion The statements which have the truth value is called premise Then, using logical principle it can be drawn a new statement ( conclusion) Drawing conclusion is also called argumentation An argumentation is called legal if the premises are true, then the conclusion are also true Hal. : LOGIKA Adaptif

Penarikan kesimpulan Pernyataan yang diketahui nilai kebenarannya disebut premis Kemudian dengan menggunakan prinsip logika dapat diturunkan pernyataan baru (kesimpulan/ konklusi) Penarikan kesimpulan tersebut sering juga disebut argumentasi Suatu argumentasi dikatakan sah jika premis-premisnya benar, maka konklusinya juga benar Hal. : LOGIKA Adaptif
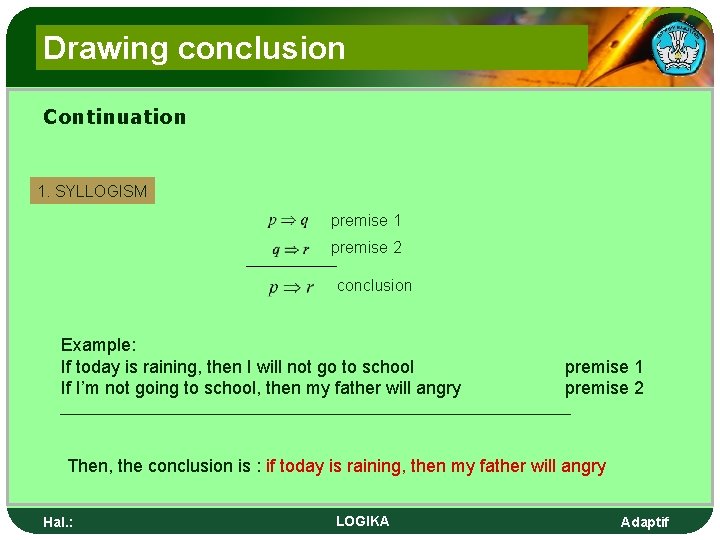
Drawing conclusion Continuation 1. SYLLOGISM premise 1 premise 2 conclusion Example: If today is raining, then I will not go to school If I’m not going to school, then my father will angry premise 1 premise 2 Then, the conclusion is : if today is raining, then my father will angry Hal. : LOGIKA Adaptif

Penarikan kesimpulan Lanjutan 1. SILLOGISME premis 1 premis 2 kesimpulan/konklusi Contoh: Jika hari ini hujan, maka saya tidak berangkat ke sekolah Jika saya tidak berangkat sekolah, maka ayah akan marah premis 1 premis 2 Maka konklusinya adalah: Jika hari ini hujan, maka ayah akan marah Hal. : LOGIKA Adaptif
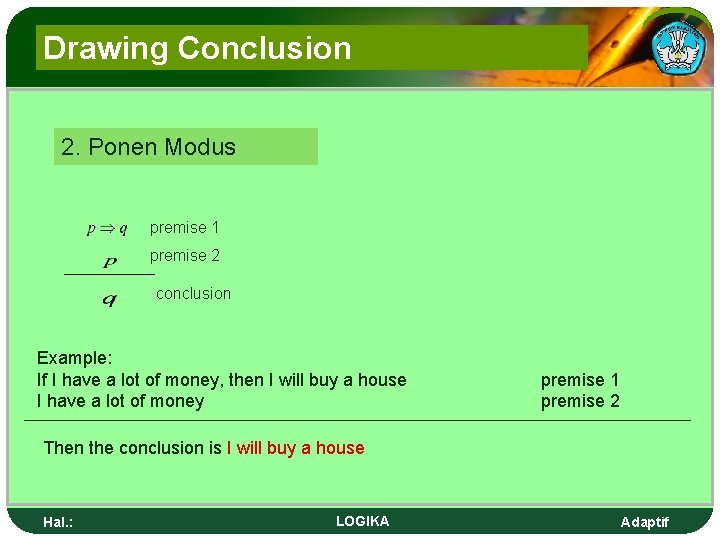
Drawing Conclusion 2. Ponen Modus premise 1 premise 2 conclusion Example: If I have a lot of money, then I will buy a house I have a lot of money premise 1 premise 2 Then the conclusion is I will buy a house Hal. : LOGIKA Adaptif

Penarikan kesimpulan 2. Modus ponen premis 1 premis 2 kesimpulan/konklusi Contoh: Jika saya punya uang banyak, maka saya akan membeli rumah Saya punya uang banyak premis 1 premis 2 Maka konklusinya adalah Saya akan membeli rumah Hal. : LOGIKA Adaptif
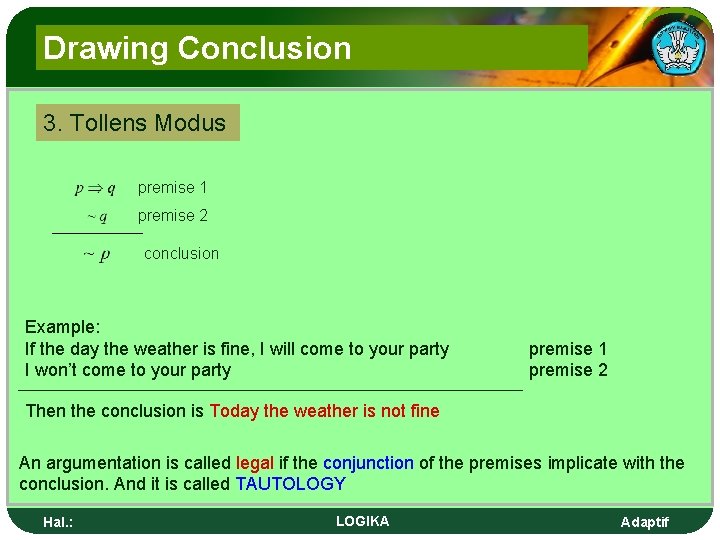
Drawing Conclusion 3. Tollens Modus premise 1 premise 2 conclusion Example: If the day the weather is fine, I will come to your party I won’t come to your party premise 1 premise 2 Then the conclusion is Today the weather is not fine An argumentation is called legal if the conjunction of the premises implicate with the conclusion. And it is called TAUTOLOGY Hal. : LOGIKA Adaptif

Penarikan kesimpulan 3. Modus tollens premis 1 premis 2 kesimpulan/konklusi Contoh: Jika hari ini cuaca cerah , maka saya datang ke pestamu Saya tidak datang ke pestamu premis 1 premis 2 Maka konklusinya adalah Hari ini cuaca tidak cerah Suatu argumentasi dikatakan sah jika konjungsi dari premis-premisnya berimplikasi dengan konklusinya merupakan TAUTOLOGI Hal. : LOGIKA Adaptif
No Lazy student! Or STUDY IN THE WHOLE LIFE Hal. : LOGIKA Adaptif
Jangan Malas ATAU Belajarlah sepanjang hayat Hal. : LOGIKA Adaptif
- Slides: 46