LOGIKA MATEMATIKA Pernyataan Tautologi Kontradiksi dan Kontingensi Pernyataan

LOGIKA MATEMATIKA

Pernyataan Tautologi, Kontradiksi, dan Kontingensi Pernyataan Majemuk Pernyataan Berkuantor Konvers, Invers, dan Kontraposisi Penarikan Kesimpulan

A. Pernyataan (kalimat tertutup): suatu kalimat yang mempunyai nilai benar saja atau salah saja, tetapi tidak sekaligus benar dan salah Kalimat terbuka: suatu kalimat yang belum dapat ditentukan nilainya benar saja atau salah saja. Karena terdapat variabel

Negasi dari pernyataan adalah suatu pernyataan baru yang diperoleh dari pernyataan semula sedemikian sehingga bernilai benar jika pernyataan semula salah dan bernilai salah jika pernyataan semula benar Menuliskan negasi suatu kalimat artinya menuliskan kata tidak atau bukan sesudah subjek atau sebelum predikat kalimat yang dinegasikan.

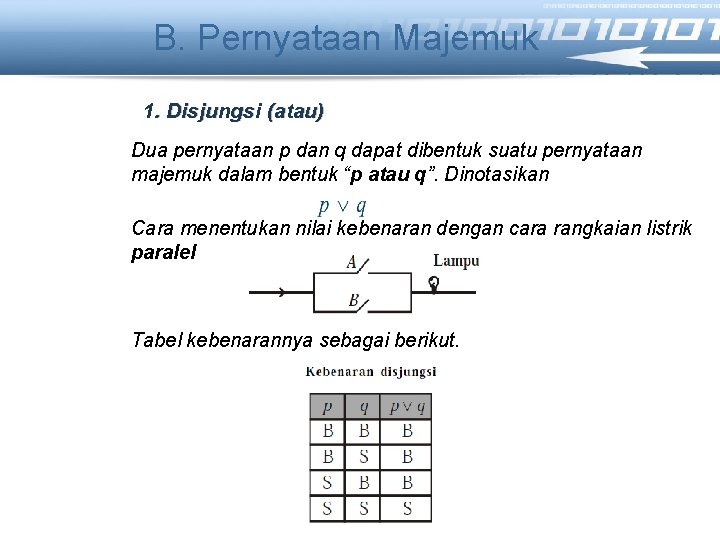
B. Pernyataan Majemuk 1. Disjungsi (atau) Dua pernyataan p dan q dapat dibentuk suatu pernyataan majemuk dalam bentuk “p atau q”. Dinotasikan Cara menentukan nilai kebenaran dengan cara rangkaian listrik paralel Tabel kebenarannya sebagai berikut.

Contoh soal Tentukan nilai kebenaran dari pernyataan majemuk berikut! a. 3 bilangan prima atau 5 bilangan genap b. 7 ‒ 2 = 9 atau 7 + 2 = 5 a. 3 bilangan prima bernilai BENAR 5 bilangan genap bernilai SALAH Karena ada yang bernilai benar, maka pernyataan majemuk “ 3 bilangan prima atau 5 bilangan genap” bernilai BENAR b. 7 ‒ 2 = 9 bernilai SALAH 7 + 2 = 5 bernilai SALAH Karena tidak ada yang bernilai benar maka pernyataan majemuk “ 7 ‒ 2 = 9 atau 7 + 2 = 5” bernilai SALAH

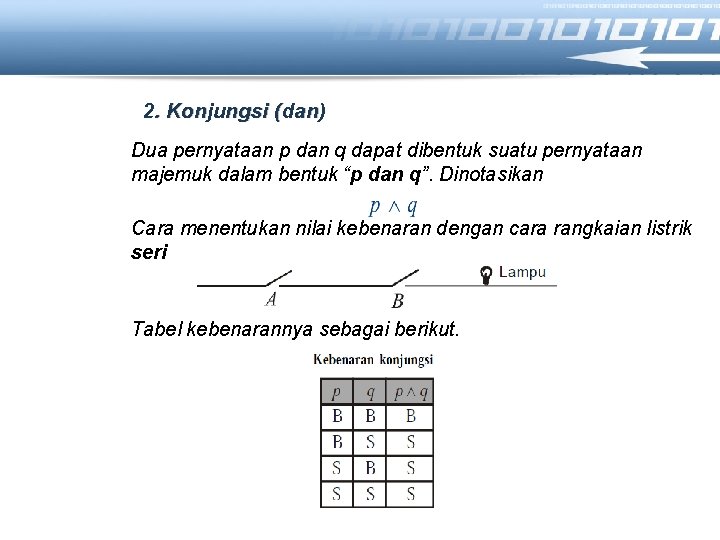
2. Konjungsi (dan) Dua pernyataan p dan q dapat dibentuk suatu pernyataan majemuk dalam bentuk “p dan q”. Dinotasikan Cara menentukan nilai kebenaran dengan cara rangkaian listrik seri Tabel kebenarannya sebagai berikut.

Contoh soal Tentukan nilai kebenaran dari pernyataan-pernyataan berikut! a. 6 bilangan prima dan 3 bilangan ganjil b. 2 bilangan prima dan 2 bilangan genap a. 6 bilangan prima bernilai SALAH 3 bilangan ganjil bernilai BENAR Karena ada yang bernilai SALAH, maka pernyataan “ 6 bilangan prima dan 3 bilangan ganjil” bernilai SALAH b. 2 bilangan prima bernilai BENAR 2 bilangan genap bernilai BENARtidak ada yang bernilai SALAH, maka pernyataan “ 2 Karena bilangan prima dan 2 bilangan genap” bernilai BENAR

2. Negasi dari Disjungsi dan Konjungsi Negasi dari disjungsi dan konjungsi adalah pernyataan baru yang nilai kebenarannya berlawanan dengan disjungsi dan konjungsi Berlawanan Dengan demikian Berlawanan

Contoh soal Tentukan negasi dari: a. Ali makan atau Tuti menangis b. 2 + 3 = 5 dan 2 × 3 = 6 a. Negasi dari “Ali makan atau Tuti menangis” adalah “Ali tidak makan dan Tuti tidak menangis” b. Negasi dari “ 2 + 3 = 5 dan 2 × 3 = 6” adalah “ 2 + 3 ≠ 5 atau 2 × 3 ≠ 6”

4. Implikasi Dua pernyataan p dan q dapat dibentuk suatu pernyataan majemuk dalam bentuk “jika p maka q”. Dinotasikan Tabel kebenarannya sebagai berikut.

Contoh soal Tentukan nilai kebenaran pernyataan majemuk berikut! a. Jika 2 + 3 = 5, maka 4 + 5 = 7 b. Jika 2 + 2 = 6, maka 3 + 2 = 5

5. Biimplikasi Dua pernyataan p dan q dapat dibentuk suatu pernyataan majemuk dalam bentuk “p jika dan hanya jika q”. Dinotasikan Tabel kebenarannya sebagai berikut.

Contoh soal Tentukan nilai kebenaran pernyataan-pernyataan berikut! a. 2 + 2 = 4 3+4=8 b. 2 + 3 = 6 2+4=8

Biimplikasi mempunyai makna ekuivalen. Ekuivalen dinotasikan “Contoh ≡” soal sama

6. Negasi dari Implikasi dan Biimplikasi Dengan menggunakan tabel kebenaran maka diperoleh sama Dengan demikian berlawanan

Contoh soal Tentukan negasi dari : a. Jika Ali pergi maka Tuti menangis b. 2 + 2 = 4 3+3=6 a. Negasi dari “Jika Ali pergi, maka Tuti menangis” adalah “Ali pergi dan Tuti tidak menangis”

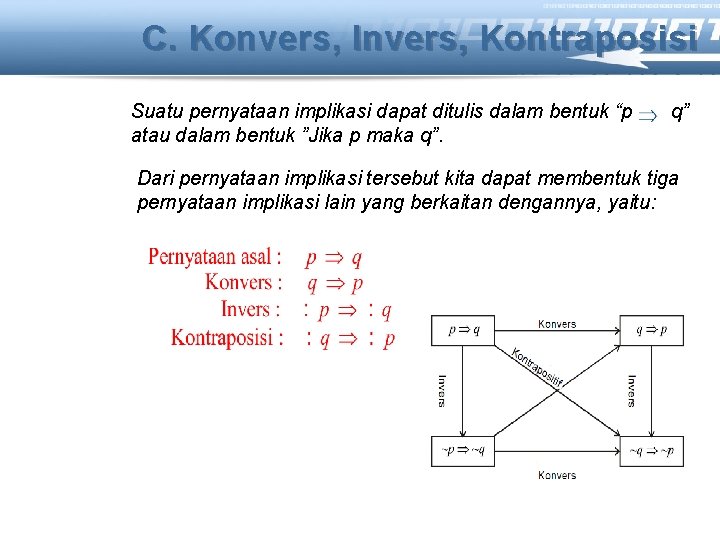
C. Konvers, Invers, Kontraposisi Suatu pernyataan implikasi dapat ditulis dalam bentuk “p atau dalam bentuk ”Jika p maka q”. q” Dari pernyataan implikasi tersebut kita dapat membentuk tiga pernyataan implikasi lain yang berkaitan dengannya, yaitu:

Contoh soal Tuliskan konvers, invers, dan kontraposisi dari pernyataan “Jika saya makan, maka saya kenyang”! Pernyataan asal : Jika saya makan, maka saya kenyang Konvers : Jika saya kenyang, maka saya makan Invers : Jika saya tidak makan, maka saya tidak kenyang Kontrapositif : Jika saya tidak kenyang, maka saya tidak makan

Tunjukkan dalam tabel kebenaran bahwa implikasi dan kontraposisi mempunyai nilai kebenaran yang sama (ekuivalen) sama Implikasi ekuivalen kontraposisi.

D. Tautologi, Kontradisi, dan Kontingensi Pernyataan majemuk yang selalu bernilai benar disebut tautologi dan yang selalu bernilai salah disebut kontradiksi. Pernyataan majemuk yang bukan tautologi atau kontradiksi disebut kontingensi.

Contoh soal Nyatakan pernyataan-pernyataan di bawah ini merupakan tautologi, kontradiksi, atau kontingensi! a. Semua nilai kebenarannya salah sehingga merupakan kontradiksi b. Pada pernyataan terdapat nilai benar dan salah sehingga kontingensi c. Semua nilai keberarannya benar sehingga merupakan tautologi

E. Pernyataan Berkuantor Kuantor berarti pengukur kuantitas atau jumlah. Kata yang merupakan kuantor di antaranya semua, seluruh, setiap, tanpa kecuali, ada, beberapa, dan sebagainya KUANTOR KHUSUS (EKSISTENSIAL) KUANTOR UMUM (UNIVERSAL)

1. Kuantor Khusus (eksistensial) Kuantor khusus (kuantor eksistensial) artinya pengukur jumlah yang menunjukkan keberadaan. Contohnya ada, beberapa, terdapat, atau sekurang-kurangnya satu. Kuantor khusus dilambangkan dengan Jika P(x) adalah kalimat terbuka pada suatu himpunan semesta S, maka dengan menambahkan kuantor khusus akan diperoleh pernyataan: dibaca ada x anggota S sehingga berlaku P(x).

Contoh soal Tentukan nilai kebenaran dari: “Beberapa binatang berkaki dua” Karena beberapa binatang seperti ayam, bebek, merpati berkaki dua, maka pernyataan “Beberapa binatang berkaki dua” bernilai benar.

2. Kuantor Umum (universal) Contoh kuantor umum(kuantor universal) di antaranya untuk semua, untuk setiap, untuk tiap-tiap, seluruh, atau tanpa kecuali. Kuantor umum dilambangkan dengan Jika P(x) adalah kalimat terbuka pada suatu himpunan semesta S, maka dengan menambahkan kuantor umum akan diperoleh pernyataan: dibaca semua x anggota S sehingga berlaku P(x).

Contoh soal Tentukan nilai kebenaran dari:

3. Negasi Pernyataan Kuantor Negasi (ingkaran) pernyataan berkuantor dapat ditentukan dengan mudah yakni dengan menambahkan kata tidak di depan kuantor. Contoh soal Tentukan negasi dari pernyataan: a. Semua siswa memakai seragam b. Ada bilangan prima yang genap a. p : Semua siswa memakai seragam ~p : Tidak semua siswa memakai seragam b. q : Ada bilangan prima yang genap ~q : Tidak ada bilangan prima yang genap

Bentuk lain dari negasi pernyataan berkuantor dapat diperoleh dengan bantuan diagram venn Tentukan negasi dari pernyataan : a. Semua A adalah B b. Ada A merupakan B a. Misalkan: p = Semua A adalah B ~p = Tidak semua A adalah B Dari diagram venn di atas: pernyataan “tidak semua A adalah B” ekuivalen dengan “ada A yang bukan B”.

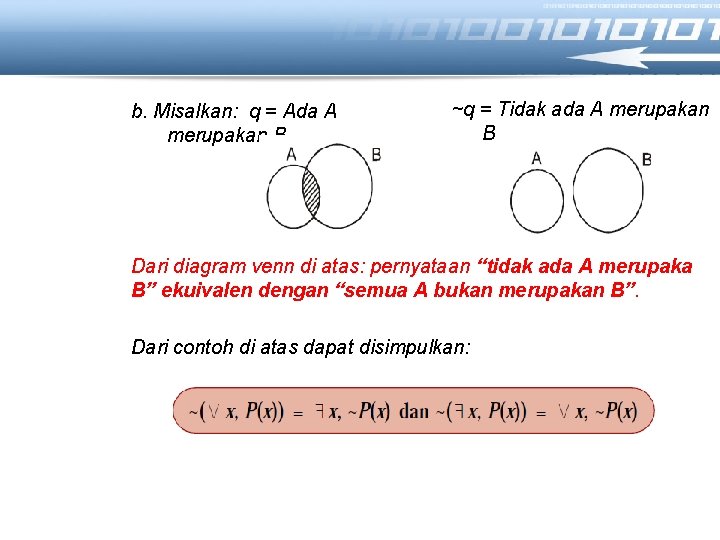
b. Misalkan: q = Ada A merupakan B ~q = Tidak ada A merupakan B Dari diagram venn di atas: pernyataan “tidak ada A merupaka B” ekuivalen dengan “semua A bukan merupakan B”. Dari contoh di atas dapat disimpulkan:

Contoh soal Tentukan negasi pernyataan: a. Semua segitiga sama sisi merupakan segitiga sama kaki b. Ada pohon pisang sedang berbuah a. p : Semua segitiga sama sisi merupakan segitiga sama kaki ~p : Tidak semua segitiga sama sisi merupakan segitiga sama kaki ~p : Ada segitiga sama sisi bukan merupakan segitiga sama kaki

Lanjutan b. q : Ada pohon pisang sedang berbuah ~q : Tidak ada pohon pisang sedang berbuah ~q : Semua pohon pisang tidak sedang berbuah

F. Penarikan Kesimpulan Proses penarikan kesimpulan dikatakan sah (valid) jika implikasi dari konjungsi premis-premis dengan kesimpulan atau konklusi merupakan tautologi 1. Modus Ponens Jika p q bernilai benar dan p bernilai benar, maka dari tabel didapat bahwa q bernilai benar. Rumusan modus ponens tersebut ditulis sebagai: Premis 1 : Jika p maka q (benar) Premis p 2: atau (benar) Konklusi : q (benar)

Contoh soal Tentukan kesimpulan dari pernyataan-pernyataan berikut! Jika x bilangan prima maka x mempunyai dua faktor, 7 bilangan prima. Premis 1 : Jika x bilangan prima maka x mempunyai dua faktor Premis 2 : 7 bilangan prima Konklusi : 7 mempunyai dua faktor.

2. Modus Tollens Jika p q bernilai benar dan ~q bernilai benar (q bernilai salah), maka dari tabel didapat bahwa ~p bernilai benar. Rumusan modus tollens tersebut ditulis sebagai: Premis 1 : Jika p maka q (benar) Premis 2 : ~q (benar) Konklusi : ~q (benar) atau

Contoh soal Tentukan kesimpulan dari pernyataan-pernyataan berikut! Jika suatu segitiga sama sisi maka segitiga tersebut sama kaki, segitiga ABC tidak sama kaki Premis 1 : Jika suatu segitiga samasisi, maka segitiga tersebut samakaki Premis 2 : Segitiga ABC tidak samakaki Konklusi : samasisi Segitiga ABC tidak

3. Silogisme Jika p maka q bernilai benar dan jika q maka r bernilai benar, maka jika p maka r bernilai benar. Rumusan silogisme tersebut ditulis sebagai berikut Premis 1 : Jika p maka q (benar) Premis 2 : Jika q maka r (benar) Konklusi : Jika p maka r (benar) atau

Thank You !!!