Logika dan Sistem Digital ALJABAR BOOELAN Tujuan Perkuliahan

Logika dan Sistem Digital ALJABAR BOOELAN

Tujuan Perkuliahan Mahasiswa dapat memahami dan menjelaskan tentang : • Latar Belakang dan Hukum Aljabar Boolean • Fungsi Boolean • Bentuk Kanonik SOP dan POS

Agenda Chapter 1 – Aljabar Boolean 1. Pendahuluan Aljabar Boolean 2. Hukum Aljabar Boolean 3. Penyederhanaan Dengan Aljabar Boolean Chapter 2 – Fungsi Kanonik

History Aljabar Boolean Cabang matematika George Boole • George Boole memaparkan aturan-aturan dasar logika (dikenal dengan Logika Boolean) • Tahun 1938, Claude Shannon memperlihatkan penggunaan Aljabar Boolean untuk merancang rangkaian sirkuit yang menerima masukan 0 dan 1 1854 • Aljabar Boolean digunakan secara luas dalam perancangan rangkaian pensaklaran, rangkaian digital dan rangkaian IC komputer

Postulat Boolean Dalam mengembangkan sistem Aljabar Boolean perlu memulainya dengan asumsi – asumsi yakni Postulat Boolean dan Teorema Aljabar Boolean. 0. 0=0 0. 1=0 1. 0=0 1. 1=1 0+0=0 0+1=1 1+0=1 1+1=1 =1 =0 di turunkan dari fungsi AND. di turunkan dari fungsi OR. di turunkan dari fungsi NOT.

Prinsip Dualitas Dalil Aljabar Boolean dan Prinsip Dualitas • Aljabar Boolean menggunakan aturan-aturan yang diturunkan dari asumsi dasar (aksioma/dalil/postulat). 1 x. 2 x. 3 x. 4 x. 0. 0=0 1. 1=1 0. 1=1. 0=0 Jika a = 0 , maka a’ = 1 1 y. 2 y. 3 y. 4 y. 1+1=1 0+0=0 1+0=0+1=1 Jika a = 1 , maka a’ = 0 • Dalil dituliskan berpasangan untuk menunjukkan prinsip dualitas. - Jika diberikan sebarang ekspresi logika, dual dari ekspresi tersebut dapat dibentuk dengan mengganti semua (+) dengan (. ) atau sebaliknya, serta mengganti 0 dengan 1 atau sebaliknya. - Dalil (y) merupakan dual dari dalil (x) dan sebaliknya - Dual dari pernyataan benar adalah juga benar

Hukum Aljabar Boolean (1) Berikut ini adalah hukum-hukum aljabar boolean : 1. Hukum identitas: (i). a+0=a (ii). a 1 = a 2. Hukum idempoten: (i). a + a = a (ii). a a = a 3. Hukum komplemen: (i). a + a’ = 1 (ii). a. a’ = 0 4. Hukum dominansi: (i). a. 0 = 0 (ii). a + 1 = 1 5. Hukum involusi: (i). (a’)’ = a 6. Hukum penyerapan: (i) a + a. b = a a + a. b’ = a (ii) a. (a + b) = a 7. Hukum komutatif: (i). a + b = b + a (ii). a. b = b. a 8. Hukum asosiatif: (i). a + (b + c) = (a + b) + c (ii). a. (b. c) = (a. b). c 9. Hukum distributif: (i). a + (b. c) = (a + b). (a + c) (ii). a. (b + c) = a. b + a. c 10. Hukum De Morgan: (i). (a + b)’ = a’. b’ (ii). (a. b)’ = a’ + b’ 11. Hukum 0/1 (i). 0’ = 1 (ii). 1’ = 0 12. Penggabungan (i). a. b + a. b’ = a (ii). ( a + b’ ) = a

Hukum Aljabar Boolean (2) Pembuktian Hukum 6. (i) dengan cara induksi adalah sbb : • Tabel kebenaran untuk a + a. b = a a b a+a. b 0 0 0 1 1 1 Dari tabel diatas nila a + a. b = a

Hukum Aljabar Boolean (3) Contoh Kasus : Sederhanakan : a. (a. b+c) Penyelesaian : a. (a. b+c) =a. a. b+a. c =a. (b+c) (Distributif) (Idempoten) (Distributif)

Aljabar Boolean (1) Pembuktian hukum aljabar boolean dengan perhitungan aljabar : Buktikan bahwa : (i) a + a’. b = a + b (ii) a. (a’ + b) = a. b Penyelesaian : (i) a + a’. b = (a + a. b) + a’. b = a + (a. b + a’. b) = a + (a + a’). b =a+1. b =a+b (ii) adalah dual dari (i) (Penyerapan) (Asosiatif) (Distributif) (Komplemen) (Identitas)

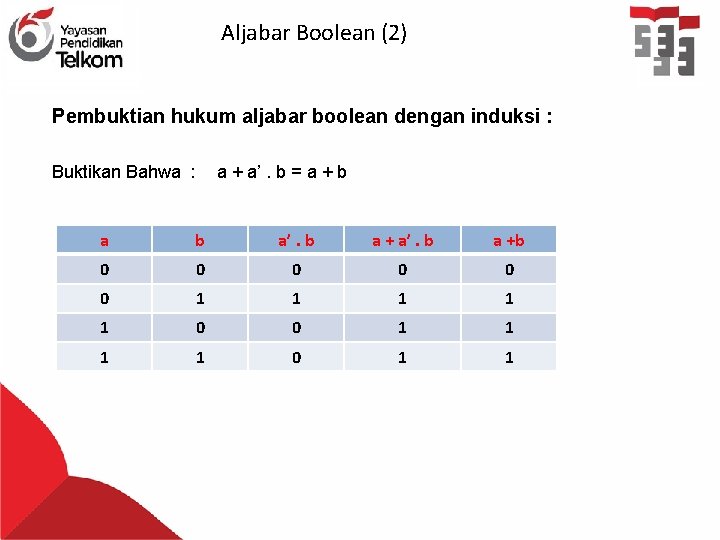
Aljabar Boolean (2) Pembuktian hukum aljabar boolean dengan induksi : Buktikan Bahwa : a + a’. b = a + b a’. b a +b 0 0 0 1 1 1 0 0 1 1

Aljabar Boolean (3) Penyederhanaan Rangkaian dengan Aljabar Suatu fungsi logika dapat dinyatakan dalam beberapa bentuk ekspresi yang ekivalen • Misalnya ada 2 aljabar : (i). a’. b’ + a’. b + a. b (ii). a’ + b (i) dan (ii) adalah ekivalen secara fungsional • Proses optimasi memilih salah satu dari beberapa rangkaian ekivalen untuk memenuhi constraint nonfungsional (area, cost) • a’. b’ + a’. b + a. b atau • a’. b’ + a’. b + a. b (replikasi term 2 ) a’. ( b’ + b ) + ( a’ + a ). b (distributif) a’. 1 + 1. b (komplemen) a’ + b a b

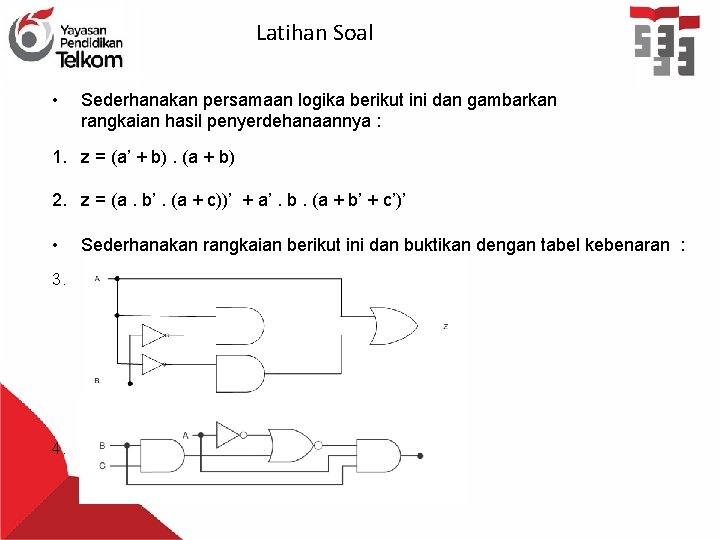
Latihan Soal • Sederhanakan persamaan logika berikut ini dan gambarkan rangkaian hasil penyerdehanaannya : 1. z = (a’ + b). (a + b) 2. z = (a. b’. (a + c))’ + a’. b. (a + b’ + c’)’ • 3. 4. Sederhanakan rangkaian berikut ini dan buktikan dengan tabel kebenaran :

Agenda Chapter 1 – Aljabar Boolean Chapter 2 – Fungsi Kanonik 1. Definisi Fungsi Boolean 2. Bentuk Kanonik SOP 3. Bentuk Kanonik POS

Fungsi Boolean (1) Definisi Fungsi Boolean Persamaan (ekspresi ) aljabar yang dibentuk dari variabel Variabel biner, operator biner ( OR dan AND ), Operator Unary ( NOT ), Dan Tanda sama dengan ( = ) Contoh : F = a. b’. c Keterangan : F = Fungsi Boolean

Fungsi Boolean (2) Lateral Dan Term • Lateral : menyatakan input – input sebuah gerbang logika • Term : menyatakan operasi yang dilakukan dalam sebuah gerbang Contoh : F = a. b. c’ + a’. d. e Keterangan : • Persamaan Boolean di atas mempunyai 5 input (ada 5 lateral : a, b, c, d dan e) • Ada 5 term : - AND untuk a. b. c’ - AND untuk a’. d. e - NOT untuk c - NOT untuk a - OR untuk f berarti ada 5 gerbang yang diperlukan

Bentuk Kanonik SOP (1) Minterm • Untuk sebuah fungsi dengan n buah variabel f(a 1 , a 2, a 3. . . an) - Sebuah minterm dari f adalah satu term perkalian dari n variabel yang ditampilkan sekali, baik dalam bentuk tidak diinverskan maupun diinverskan - Jika diberikan satu baris dalam tabel kebenaran, minterm dibentuk dengan memasukkan variabel ai jika ai = 1 atau ai’ jika ai = 0 - Notasi mj merupakan minterm dari baris nomor j di tabel kebenaran. Contoh: - Baris 1 ( j = 0 ), a 1 = 0, a 2 = 0, a 3 = 0 minterm : mo = a 1‘. a 2‘. a 3‘ - Baris 2 ( j = 1 ), a 1 = 0, a 2 = 0, a 3 = 1 minterm : m 1 = a 1‘. a 2‘. a 3

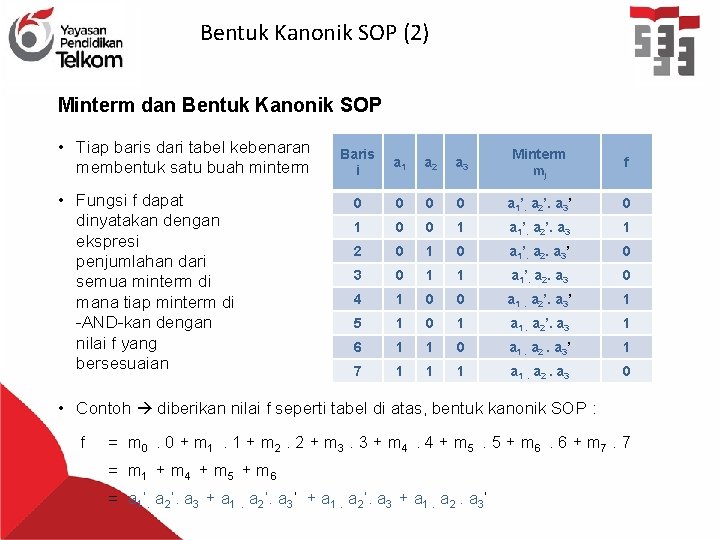
Bentuk Kanonik SOP (2) Minterm dan Bentuk Kanonik SOP • Tiap baris dari tabel kebenaran membentuk satu buah minterm • Fungsi f dapat dinyatakan dengan ekspresi penjumlahan dari semua minterm di mana tiap minterm di -AND-kan dengan nilai f yang bersesuaian Baris i a 1 a 2 a 3 Minterm mj f 0 0 a 1’. a 2’. a 3’ 0 1 0 0 1 a 1’. a 2’. a 3 1 2 0 1 0 a 1’. a 2. a 3’ 0 3 0 1 1 a 1’. a 2. a 3 0 4 1 0 0 a 1. a 2’. a 3’ 1 5 1 0 1 a 1. a 2’. a 3 1 6 1 1 0 a 1. a 2. a 3’ 1 7 1 1 1 a 1. a 2. a 3 0 • Contoh diberikan nilai f seperti tabel di atas, bentuk kanonik SOP : f = m 0. 0 + m 1. 1 + m 2. 2 + m 3. 3 + m 4. 4 + m 5. 5 + m 6. 6 + m 7. 7 = m 1 + m 4 + m 5 + m 6 = a 1’. a 2’. a 3 + a 1. a 2’. a 3’ + a 1. a 2’. a 3 + a 1. a 2. a 3’

Bentuk Kanonik SOP (3) Notasi SOP • Persamaan SOP dapat dinyatakan dalam notasi m f = m 1 + m 4 + m 5 + m 6 = a 1’. a 2’. a 3 + a 1. a 2’. a 3’ + a 1. a 2’. a 3 + a 1. a 2. a 3’ 1 4 5 6 • Notasi Persamaan SOP : f = Σ m ( 1; 4; 5; 6) • Implementasi : - Ekspresi fungsi f tersebut secara fungsional benar dan unik - Namun, mungkin tidak menghasilkan implementasi yang paling sederhana

Bentuk Kanonik POS (1) Prinsip Duality SOP - POS • Jika suatu fungsi f dinyatakan dalam suatu tabel kebenaran, maka ekspresi untuk f dapat diperoleh (disintesis) dengan cara : 1. Melihat semua baris dalam tabel dimana f=1 2. Melihat semua baris dalam tabel dimana f=0 • Pendekatan (1) menggunakan minterm • Pendekatan (2) menggunakan komplemen dari minterm, disebut maxterm

Bentuk Kanonik POS (2) Penjelasan Dualitas SOP - POS • Jika fungsi f dinyatakan dalam tabel kebenaran, maka fungsi inversnya f’ , dapat dinyatakan dengan penjumlahan minterm dengan f’ = 1, yaitu di baris di mana f = 0 f’ = m 0 + m 2 + m 3 + m 7 = a 1’. a 2’. a 3’ + a 1’. a 2. a 3 + a 1. a 2. a 3 • Fungsi f dapat dinyatakan f = ( m 0 + m 2 + m 3 + m 7 )’ = ( a 1’. a 2’. a 3’ + a 1’. a 2. a 3 + a 1. a 2. a 3 )’ = ( a 1’. a 2’. a 3’ )’. ( a 1’. a 2. a 3 )’. ( a 1. a 2. a 3 )’ = ( a 1 + a 2 + a 3 ). ( a 1 + a 2’ + a 3’ ). ( a 1’ + a 2’ + a 3’ ) • Meletakkan dasar untuk menyatakan fungsi sebagai bentuk perkalian semua term perjumlahan, maxterm

Bentuk Kanonik POS (3) Maxterm • Untuk sebuah fungsi dengan n buah variabel f(a 1 , a 2, a 3. . . an) - Sebuah maxterm dari f adalah satu term penjumlahan dari n variabel yang ditampilkan sekali, baik dalam bentuk tidak diinverskan maupun diinverskan - Jika diberikan satu baris dalam tabel kebenaran, maxterm dibentuk dengan memasukkan variabel ai jika ai = 0 atau ai’ jika ai = 1 - Notasi Mj (dengan huruf besar) merupakan maxterm dari baris nomor j di tabel kebenaran. Contoh: - Baris 1 ( j = 0 ), a 1 = 0, a 2 = 0, a 3 = 0 minterm : Mo = a 1 + a 2 + a 3 - Baris 2 ( j = 1 ), a 1 = 0, a 2 = 0, a 3 = 1 minterm : M 1 = a 1 + a 2 + a 3‘

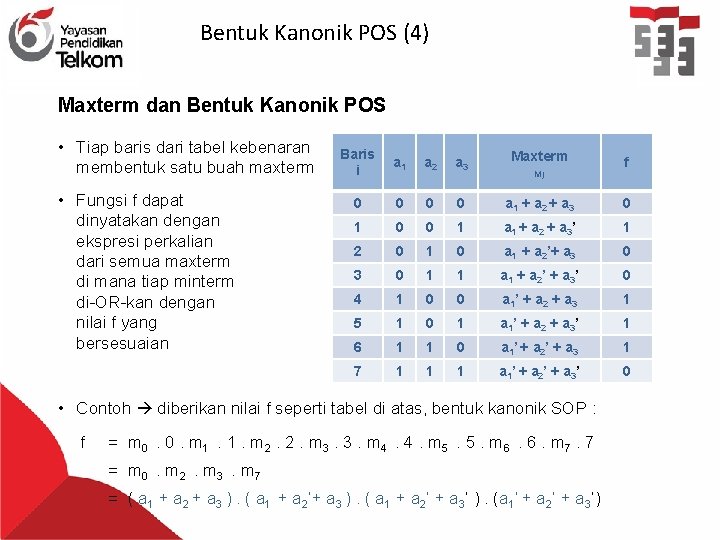
Bentuk Kanonik POS (4) Maxterm dan Bentuk Kanonik POS • Tiap baris dari tabel kebenaran membentuk satu buah maxterm • Fungsi f dapat dinyatakan dengan ekspresi perkalian dari semua maxterm di mana tiap minterm di-OR-kan dengan nilai f yang bersesuaian Baris i a 1 a 2 a 3 Maxterm 0 0 a 1 + a 2 + a 3 0 1 0 0 1 a 1 + a 2 + a 3’ 1 2 0 1 0 a 1 + a 2’+ a 3 0 1 1 a 1 + a 2’ + a 3’ 0 4 1 0 0 a 1’ + a 2 + a 3 1 5 1 0 1 a 1’ + a 2 + a 3’ 1 6 1 1 0 a 1’ + a 2’ + a 3 1 7 1 1 1 a 1’ + a 2’ + a 3’ 0 Mj • Contoh diberikan nilai f seperti tabel di atas, bentuk kanonik SOP : f = m 0. 0. m 1. 1. m 2. 2. m 3. 3. m 4. 4. m 5. 5. m 6. 6. m 7. 7 = m 0. m 2. m 3. m 7 = ( a 1 + a 2 + a 3 ). ( a 1 + a 2’ + a 3’ ). (a 1’ + a 2’ + a 3’) f

Bentuk Kanonik POS (5) Notasi POS • Persamaan POS dapat dinyatakan dalam notasi M f = m 0 + m 2 + m 3 + m 7 = ( a 1 + a 2 + a 3 ). ( a 1 + a 2’ + a 3’ ). (a 1’ + a 2’ + a 3’) 0 2 3 7 • Notasi Persamaan POS : f = Π M ( 0; 2; 3; 7) • Persamaan berikut benar untuk fungsi f(a 1, a 2, a 3) di atas : Σ m ( 1; 4; 5; 6) = Π M ( 0; 2; 3; 7) a 1’. a 2’. a 3 + a 1. a 2’. a 3’ + a 1. a 2’. a 3 + a 1. a 2. a 3’ = ( a 1 + a 2 + a 3 ). ( a 1 + a 2’ + a 3’ ). (a 1’ + a 2’ + a 3’)

Konversi Bentuk SOP dan POS • Jika suatu fungsi f diberikan dalam bentuk Σ m atau Π M , maka dengan mudah dapat dicari fungsi f atau f’ dalam bentuk Σ m atau Π M

Contoh Kasus • Operasi penyederhanaan adalah mengurangi minterm atau maxterm di ekspresi - SOP : menggunakan hukum penggabungan 12 (i) a. b + a. b’ = a - POS : menggunakan hukum penggabungan 12 (ii) ( a + b ). ( a + b’ ) = a • Beberapa minterm atau maxterm dapat digabungkan menggunakan hukum 12 (i) atau 12 (ii) jika berbeda hanya di satu variabel saja f = a 1’. a 2’. a 3 + a 1. a 2’. a 3’ + a 1. a 2’. a 3 + a 1. a 2. a 3’ - m 1 dan m 5 berbeda di a 1, dan m 4 dan m 6 berbeda di a 2 Contoh : . . f = ( a 1 + a 2 + a 3 ). ( a 1 + a 2’ + a 3’ ). (a 1’ + a 2’ + a 3’) - m 0 dan m 2 berbeda di a 2, dan m 3 dan m 7 berbeda di a 1 Contoh : . .

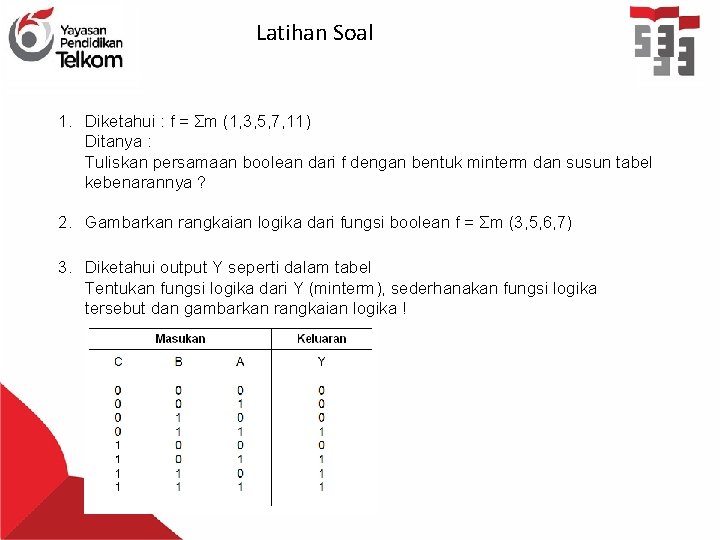
Latihan Soal 1. Diketahui : f = Σm (1, 3, 5, 7, 11) Ditanya : Tuliskan persamaan boolean dari f dengan bentuk minterm dan susun tabel kebenarannya ? 2. Gambarkan rangkaian logika dari fungsi boolean f = Σm (3, 5, 6, 7) 3. Diketahui output Y seperti dalam tabel Tentukan fungsi logika dari Y (minterm), sederhanakan fungsi logika tersebut dan gambarkan rangkaian logika !

Penutup Perkuliahan Mahasiswa telah dapat memahami dan menjelaskan tentang : • Latar Belakang Aljabar Boolean History, Postulat, Dan Prinsip Dualits • Hukum Aljabar Boolean Hukum-Hukum Aljabar Boolean, Penyederhanaan Rangkaian Denga Aljabar • Bentuk Kanonik SOP dan POS Minterm, Maxterm, Konversi Bentuk SOP dan POS

Thank You