Logics for Data and Knowledge Representation Description Logics

Logics for Data and Knowledge Representation Description Logics

Outline q Overview q Syntax: the DL family of languages q Semantics q TBox q ABox q Tableau 2 Algorithm

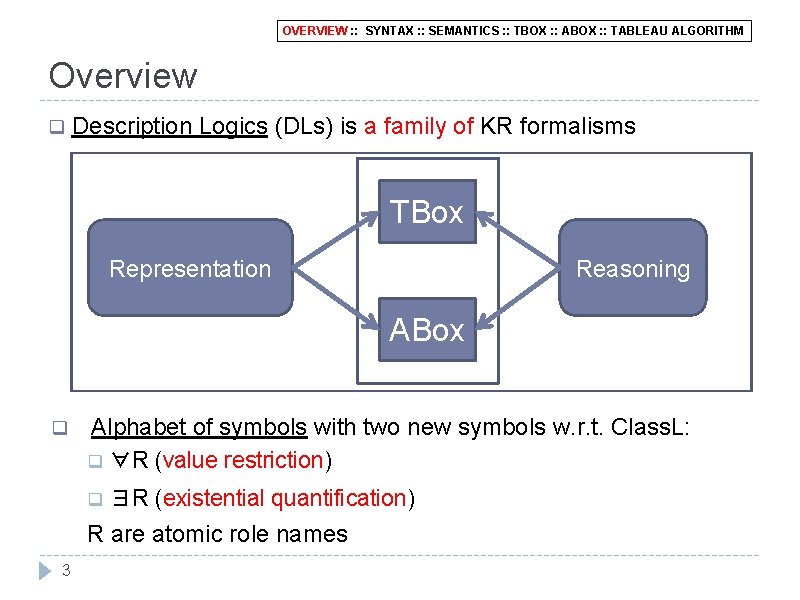
OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Overview q Description Logics (DLs) is a family of KR formalisms TBox Representation Reasoning ABox q Alphabet of symbols with two new symbols w. r. t. Class. L: q ∀R (value restriction) q ∃R (existential quantification) R are atomic role names 3

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM AL (Attributive language) q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬<Atomic> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ with no ⊔, ∃R. ⊤ = limited existential quantifier, ¬ on atomic only q q 4 Person ⊓ Female “persons that are female” Person ⊓ ∃has. Child. ⊤ “(all those) persons that have a child” Person ⊓ ∀has. Child. ⊥ “(all those) persons without a child” Person ⊓ ∀has. Child. Female “persons all of whose children are female”

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ALU (AL with disjunction) q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬<Atomic> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ | <wff> ⊔ <wff> with ⊔ q Person ⊓ (Mother ⊔ Father) “the people who are parents” q Apple ⊓ (Red ⊔ Yellow) “red and yellow apples” 5

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ALE (AL with extended existential) q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬<Atomic> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ | ∃R. C with ∃R. C (full existential quantification) q Parent ⊓ ∃has. Child. Female “parents having at least a daughter” 6

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ALN (AL with number restriction) q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬<Atomic> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ | ≥n. R | ≤n. R ≥n. R (at-least number restriction) ≤n. R (at-most number restriction) q Parent ⊓ ≥ 2 has. Child “parents having at least two children” 7

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ALC (AL with full concept negation) q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬ <wff> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ with full concept negation q (Mother ⊓ Father) “it cannot be both a mother and father” 8

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM AL’s extensions q By extending AL with any subsets of the above constructors yields a particular DL language. q Each language is denoted by a string of the form: AL[U][E][N][C], where a letter in the name stands for the presence of the corresponding constructor. q 9 ALC is considered the most important for many reasons. NOTE: ALU ⊆ ALC and ALE ⊆ ALC

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM AL’s sub-languages q By eliminating some of the syntactical symbols and rules, we get some sub-languages of AL q Class. L: the most important sub-language obtained by elimination in the AL family q FL- and FL 0 (where FL = frame language) 10

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM From AL to Class. L q ALUC with the elimination of roles ∀R. C and ∃R. ⊤ q Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . | ⊥ | ⊤ <wff> : : = <Atomic> | ¬ <wff> | <wff> ⊓ <wff> | <wff> ⊔ <wff> q The new language is a description language without roles which is Class. L (also called propositional DL) NOTE: So far, we are considering DL without TBOX and ABox. 11

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM AL’s Contractions: FL- and FL 0 q q FL- is AL with the elimination of ⊤, ⊥ and Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . <wff> : : = <Atomic> | <wff> ⊓ <wff> | ∀R. C | ∃R. ⊤ q q FL 0 is FL- with the elimination of ∃R. ⊤ Formation rules: <Atomic> : : = A | B |. . . | P | Q |. . . <wff> : : = <Atomic> | <wff> ⊓ <wff> | ∀R. C 12

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM AL* Interpretation (∆, I) q I(⊥) =∅ and I(⊤) = ∆ (full domain, “Universe”) For every concept name A of L, I(A) ⊆ ∆ q I(¬C) = ∆ I(C) q I(C⊓D) = I(C) ∩ I(D) q I(C ⊔ D) = I(C) ∪ I(D) q For every role name R of L, I(R) ⊆ ∆ × ∆ q I(∀R. C) = {a ∈ ∆ | for all b, if (a, b)∈I(R) then b∈I(C)} q I(∃R. ⊤) = {a ∈ ∆ | exists b s. t. (a, b) ∈ I(R)} q I(∃R. C) q I(≥n. R) q I(≤n. R) q 13 = {a ∈ ∆ | exists b s. t. (a, b) ∈ I(R), b ∈ I(C)} = {a ∈ ∆ | |{b | (a, b) ∈ I(R)}| ≥ n} = {a ∈ ∆ | |{b | (a, b) ∈ I(R)}| ≤ n} The SAME as in Class. L

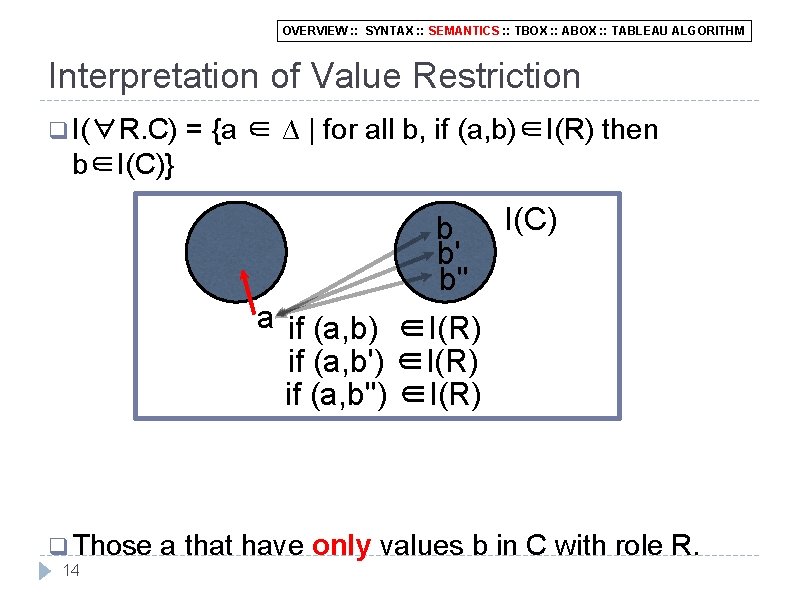
OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Interpretation of Value Restriction q I(∀R. C) = {a ∈ ∆ | for all b, if (a, b)∈I(R) then b∈I(C)} b b' b'' I(C) a if (a, b) ∈I(R) if (a, b'') ∈I(R) q Those 14 a that have only values b in C with role R.

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Interpretation of Existential Quantifier q I(∃R. C) = {a ∈ ∆ | exists b s. t. (a, b) ∈ I(R), b ∈ I(C)} b I(C) a (a, b)∈I(R) q Those 15 a that have some value b in C with role R.

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Interpretation of Number Restriction q I(≥n. R) = {a∈∆ | |{b | (a, b) ∈ I(R)}|≥ n} a ∆ b b' … |{b | (a, b) ∈ I(R)}| ≥ n q Those 16 a that have relation R to at least n individuals.

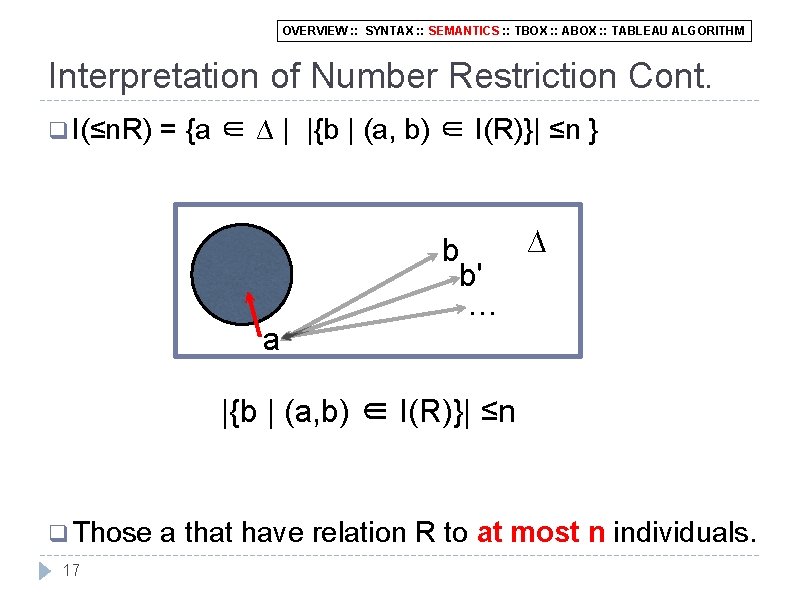
OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Interpretation of Number Restriction Cont. q I(≤n. R) = {a ∈ ∆ | |{b | (a, b) ∈ I(R)}| ≤n } a ∆ b b' … |{b | (a, b) ∈ I(R)}| ≤n q Those 17 a that have relation R to at most n individuals.

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Terminology (TBox), same as in Class. L q A terminology (or TBox) is a set of definitions and specializations q Terminological axioms express constraints on the concepts of the language, i. e. they limit the possible models q The TBox is the set of all the constraints on the possible models Equivalence TBOX Equality axiom Definition Inclusion axiom Specialization Ph. D ≡ Postgraduate ⊓ ≥ 3 Publish Parent ≡ Person ⊓ ∃has. Child. Person has. Grand. Child ⊑ has. Child Subsumption 18

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Reasoning with a TBox T, same as Class. L Given two class-propositions P and Q, we want to reason about: T⊨P? Satisfiability w. r. t. T A concept P is satisfiable w. r. t. a terminology T, if there exists an interpretation I with I ⊨ θ for all θ ∈ T, and such that I ⊨ P, I(P)≠∅ Subsumption T ⊨ P ⊑ Q? T ⊨ Q ⊑ P? A concept P is subsumed by a concept Q w. r. t. T if I(P) I(Q) for every model I of T Equivalence T ⊨ P ⊑ Q and T ⊨ Q ⊑ P? Two concepts P and Q are equivalent w. r. t. T if I(P) = I(Q) for every model I of T Disjointness T ⊨ P ⊓ Q ⊑ ⊥? Two concepts P and Q are disjoint with respect to T if their intersection is empty, I(P) I(Q) = ∅, for every model I of T 19

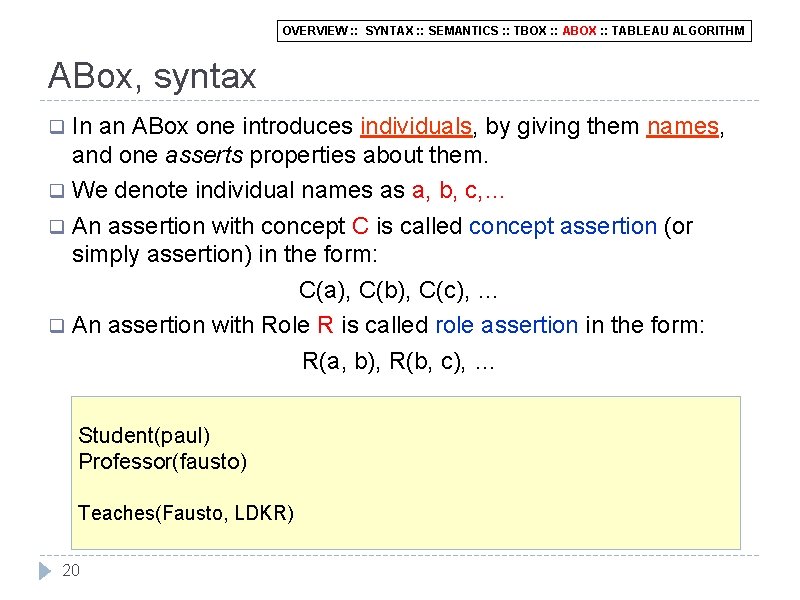
OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ABox, syntax In an ABox one introduces individuals, by giving them names, and one asserts properties about them. q We denote individual names as a, b, c, … q An assertion with concept C is called concept assertion (or simply assertion) in the form: C(a), C(b), C(c), … q An assertion with Role R is called role assertion in the form: R(a, b), R(b, c), … q Student(paul) Professor(fausto) Teaches(Fausto, LDKR) 20

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM ABox, semantics q An interpretation I: L pow(∆I) not only maps atomic concepts to sets, but in addition it maps each individual name a to an element a. I ∈ ∆I, namely I(a) = a. I ∈ ∆ I I (C(a)) = a. I ∈CI, I(R(a, b)) = (a. I, b. I)∈RI q Unique name assumption (UNA). We assume that distinct individual names denote distinct objects in the domain NOTE: ∆I denotes the domain of interpretation, a denotes the symbol used for the individual (the name), while a. I is the actual individual of the domain. 21

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Reasoning Services, same as Class. L q Given an ABox A, we can reason (w. r. t. a TBox T) about the following: q Satisfiability/Consistency: An ABox A is consistent with respect to T if there is an interpretation I which is a model of both A and T. q Instance checking: checking whether an assertion C(a) or R(a, b) is entailed by an ABox, i. e. checking whether a belongs to C. A ⊨ C(a) if every I that satisfies A also satisfies C(a). A ⊨ R(a, b) if every I that satisfies A also satisfies R(a, b). q Instance retrieval: given a concept C, retrieve all the instances a which satisfy C. Concept realization: given a set of concepts and an individual a find the most specific concept(s) C (w. r. t. subsumption ordering) such that A ⊨ C(a). q 22

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Tableaux Calculus q The Tableaux calculus is a decision procedure to check satisfiability of a DL formula. q The procedure looks for a model satisfying the formula in input q The basic idea is to incrementally build the model by looking at the formula and by decomposing it into pieces in a top-down fashion. q The procedure exhaustively tries all possibilities so that it can eventually prove that no model could be found and therefore the formula is unsatisfiable. 23

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Preview example C = (∃R. A) ⊓ (∃R. B) ⊓ (∃R. (A ⊔ B)) C = (∃R. A) ⊓ (∃R. B) ⊓ (∃R. ( A ⊓ B)) De Morgan In Negation Normal Form C is safisfiable iff I(C) ≠ ∅ for some I C 1 = ∃R. A C 2 = ∃R. B C 3 = ∃R. ( A ⊓ B) Decomposition For C 1 ∃ (b, c) ∈ I(R) and c ∈ I(A) For C 2 ∃ (b, d) ∈ I(R) and d ∈ I(B) For C 3 ∃ (b, e) ∈ I(R) and e ∈ I( A ⊓ B) e ∈ I( A) and I( B) e must be a new symbol different from c and d. The following ABox is consistent with C: {R(b, c), A(c), R(b, d), B(d), R(b, e)} 24

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM The Tableau Algorithm q The formula C in input is translated into Negation Normal Form. q An ABox A is incrementally constructed by adding assertions according to the constraints in C (identified by decomposition) following precise transformation rules Each time we have more than one option we split the space of the solutions as in a decision tree (i. e. in presence of ⊔) When a contradiction is found (i. e. A is inconsistent) we need to try another path in the space of the solutions (backtracking) q q q The algorithm stops when either we find a consistent A satisfying all the constraints in C (the formula is satisfiable) or there is no consistent A (the formula is unsatisfiable) 25

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Transformation rules q ⊓-rule Condition: A contains (C 1 ⊓ C 2)(x), but not both C 1(x) and C 2(x) Action: A’ = A ∪ {C 1(x), C 2(x)} T={Mother ≡ Female ⊓ ∃has. Child. Person} A={Mother(Anna)} Is ¬∃has. Child. Person ⊓ ¬∃has. Parent. Person) satisfiable? Expand A w. r. t. T Mother(Anna) (Female ⊓ ∃has. Child. Person)(Anna) A’ = A ∪ {Female(Anna), (∃has. Child. Person)(Anna)} (¬∃has. Child. Person ⊓ ¬∃has. Parent. Person)(Anna) A’ = A ∪ {¬∃has. Child. Person)(Anna), ¬∃has. Parent. Person)(Anna)} Both of them must be true, but the first constraint is clearly in contradiction with A’ 26

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Transformation rules q ⊔-rule Condition: A contains (C 1 ⊔ C 2)(x), but neither C 1(x) or C 2(x) Action: A’ = A ∪ {C 1(x)} and A’’ = A ∪ {C 2(x)} T={Parent≡∃has. Child. Female⊔∃has. Child. Male, Person≡Male⊔Female, Mother≡Parent ⊓Female} A={Mother(Anna)} Is ¬∃has. Child. Person satisfiable? Expand A w. r. t. T A = {Mother(Anna)} A’ = A ∪ {Parent(Anna), Female(Anna)} Parent(Anna) (∃has. Child. Female⊔∃has. Child. Male)(Anna) (∃has. Child. Female)(Anna) or (∃has. Child. Male)(Anna) Both are in contradiction with ¬∃has. Child. Person, not satisfiable. 27

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Transformation rules q ∃-rule Condition: A contains (∃R. C)(x), but there is no z such that both C(z) and R(x, z) are in A Action: A’ = A ∪ {C(z), R(x, z)} T={Parent≡∃has. Child. Female⊔∃has. Child. Male, Person≡Male⊔Female, Mother≡Parent⊓Female} A={Mother(Anna), has. Child(Anna, Bob), ¬Female(Bob)} Is ¬(∃has. Child. Person) satisfiable? Expand A w. r. t. T Mother(Anna) Parent(Anna) (∃has. Child. Female⊔∃has. Child. Male)(Anna) take (∃has. Child. Male)(Anna) has. Child(Anna, Bob), Male(Bob) … 28

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Transformation rules q ∀-rule Condition: A contains (∀R. C)(x) and R(x, z), but it does not C(z) Action: A’ = A ∪ {C(z)} T={Daughter. Parent≡∀has. Child. Female, Male⊓Female⊑⊥} A={has. Child(Anna, Bob), ¬Female(Bob)} Is Daughter. Parent satisfiable? Expand A w. r. t. T Daughter. Parent(x) ∀has. Child. Female(x) Given that has. Child(Anna, Bob) A’ = A ∪ {Female(Bob)} but this in contradiction with ¬Female(Bob) 29

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Example of Tableau Reasoning q Is ∀has. Child. Male ⊓ ∃has. Child. ¬Male satisfiable? NOTE: we do not have an initial T or A (∀has. Child. Male ⊓ ∃has. Child. ¬Male)(x) A = {(∀has. Child. Male)(x), (∃has. Child. ¬Male)(x)} ⊓-rule (∃has. Child. ¬Male)(x) A’ = A ∪ {has. Child(x, y), ¬Male(y)} ∃-rule (∀has. Child. Male)(x), has. Child(x, y) A’’ = A’ ∪ Male(y) ∀-rule A’’ is clearly inconsistent 30

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Additional Rules 31

OVERVIEW : : SYNTAX : : SEMANTICS : : TBOX : : ABOX : : TABLEAU ALGORITHM Complexity of Tableau Algorithms q The satisfiability algorithm of ALCN may need exponential time and space. It is PSPACE-complete. q An optimized algorithm needs only polynomial space as it assumes a depth-first search and stores only the ‘correct’ path. q The consistency and instance checking problem for ALCN are also PSPACE-complete. q The complexity results for other Description Logics varies according to corresponding constructors. 32