Logical Inferences Goals for propositional logic 1 Introduce





![Common fallacies 3 fallacies are common: Affirming the converse: [(p q) q] p If Common fallacies 3 fallacies are common: Affirming the converse: [(p q) q] p If](https://slidetodoc.com/presentation_image_h2/fa8c2055b27cd1b6186dafb524db4fba/image-6.jpg)
![Common fallacies. . . Assuming the antecedent: [(p q) ~p] ~q If Socrates is Common fallacies. . . Assuming the antecedent: [(p q) ~p] ~q If Socrates is](https://slidetodoc.com/presentation_image_h2/fa8c2055b27cd1b6186dafb524db4fba/image-7.jpg)




- Slides: 12

Logical Inferences Goals for propositional logic 1. Introduce notion of a valid argument & rules of inference. 2. Use inference rules to build correct arguments. Copyright © Peter Cappello

What is a rule of inference? • A rule of inference allows us to specify which conclusions may be inferred from assertions known, assumed, or previously established. • A tautology is a propositional function that is true for all values of the propositional variables (e. g. , p ~p). Copyright © Peter Cappello

Modus ponens • A rule of inference is a tautological implication. • Modus ponens: ( p (p q) ) q Copyright © Peter Cappello

Modus ponens: An example • Suppose the following 2 statements are true: • If it is 11 am in Miami then it is 8 am in Santa Barbara. • It is 11 am in Miami. • By modus ponens, we infer that it is 8 am in Santa Barbara. Copyright © Peter Cappello

Other rules of inference Other tautological implications include: (Is there a finite number of rules of inference? ) • • p (p q) p [~q (p q)] ~p [(p q) ~p] q [(p q) (q r)] (p r) hypothetical syllogism [(p q) (r s) (p r) ] (q s) [(p q) (r s) (~q ~s) ] (~p ~r) [ (p q) (~p r) ] (q r ) resolution Copyright © Peter Cappello
![Common fallacies 3 fallacies are common Affirming the converse p q q p If Common fallacies 3 fallacies are common: Affirming the converse: [(p q) q] p If](https://slidetodoc.com/presentation_image_h2/fa8c2055b27cd1b6186dafb524db4fba/image-6.jpg)
Common fallacies 3 fallacies are common: Affirming the converse: [(p q) q] p If Socrates is a man then Socrates is mortal. Therefore, Socrates is a man. Copyright © Peter Cappello
![Common fallacies Assuming the antecedent p q p q If Socrates is Common fallacies. . . Assuming the antecedent: [(p q) ~p] ~q If Socrates is](https://slidetodoc.com/presentation_image_h2/fa8c2055b27cd1b6186dafb524db4fba/image-7.jpg)
Common fallacies. . . Assuming the antecedent: [(p q) ~p] ~q If Socrates is a man then Socrates is mortal. Socrates is not a man. Therefore, Socrates is not mortal. Copyright © Peter Cappello

Common fallacies. . . • Non sequitur: p q Socrates is a man. Therefore, Socrates is mortal. • The following is valid: If Socrates is a man then Socrates is mortal. Socrates is a man. Therefore, Socrates is mortal. • The argument’s form is what matters. Copyright © Peter Cappello

Examples of arguments • Given an argument whose form isn’t obvious: • Decompose the argument into premise assertions • Connect the premises according to the argument • Check to see that the inference is valid. • Example argument: If a baby is hungry, it cries. If a baby is not mad, it doesn’t cry. If a baby is mad, it has a red face. Therefore, if a baby is hungry, it has a red face. Copyright © Peter Cappello

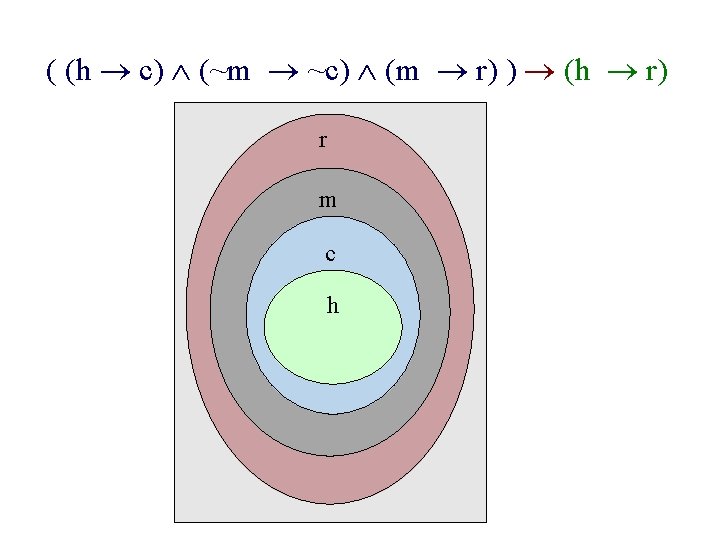
If a baby is hungry, it cries. If a baby is not mad, it doesn’t cry. If a baby is mad, it has a red face. Therefore, if a baby is hungry, it has a red face. ___________________ h: a baby is hungry c: a baby cries m: a baby is mad r: a baby has a red face. Argument: ( (h c) (~m ~c) (m r) ) (h r) Copyright © Peter Cappello 2016

( (h c) (~m ~c) (m r) ) (h r) r m c h Copyright © Peter Cappello

Examples of arguments. . . • Argument: Mc. Cain will be elected if and only if California votes for him. If California keeps its air base, Mc. Cain will be elected. Therefore, Mc. Cain will be elected. • Assertions: • m: Mc. Cain will be elected • c: California votes for Mc. Cain • b: California keeps its air base • Argument: [(m c) (b m)] m (valid? ) Copyright © Peter Cappello