Logical Form and Logical Equivalence M 260 2














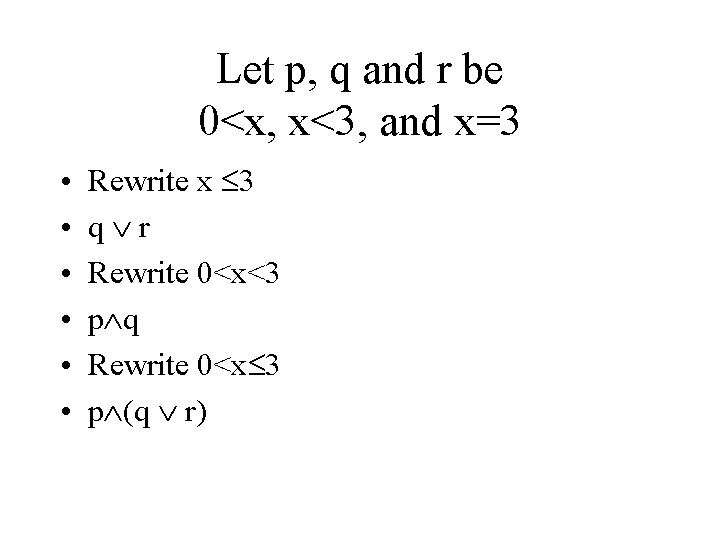











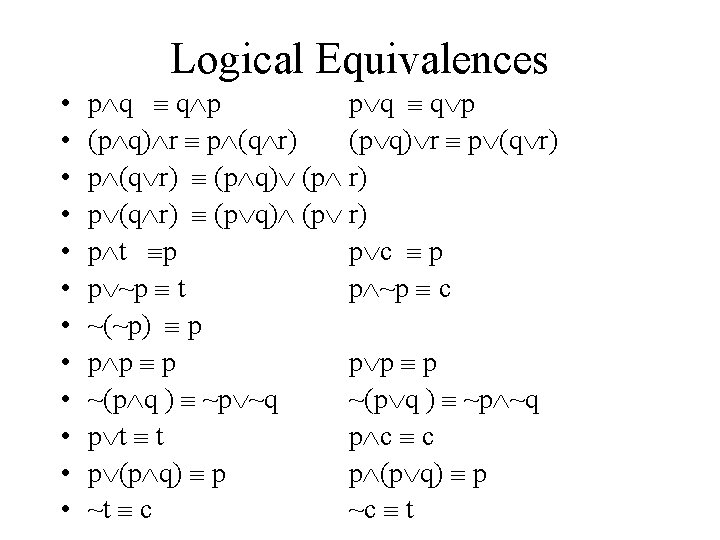
- Slides: 37

Logical Form and Logical Equivalence M 260 2. 1

Logical Form Example 1 • If the syntax is faulty or execution results in division by zero, then the program will generate an error message. • Therefore if the computer does not generate an error message then the syntax is correct and the execution does not result in division by zero.

Logical Form Example 2 • If x is a Real number such that x<-2 or x>2, then x 2>4. • Therefore if x 2 4, then x -2 and x 2.

Logical Form Example 1 • If (the syntax is faulty) or (execution results in division by zero), then (the program will generate an error message). • Therefore if (the computer does not generate an error message) then (the syntax is correct) and (the execution does not result in division by zero).

Logical Form Example 1 • If (p) or (q), then (r). • Therefore if (not r) then (not p) and (not q).

Logical Form Example 2 • If (x<-2) or (x>2), then (x 2>4). • Therefore if (x 2 4), then (x -2) and (x 2).

Logical Form Example 2 • If (p) or (q), then (r). • Therefore if (not r), then (not p) and (not q).

Logical Form vs Content • Examples 1 and 2 have the same form: If p or q, then r. therefore if not r, then not p and not q. • These examples have different values for the propositional variables p and q.

Formal Logic Goals • Avoid Ambiguity • Obtain Consistency • Elucidate Proof Mechanisms

Mathematical Vocabulary • New terms are defined using previously defined terms. • Initial terms remain undefined. • Undefined terms in logic: sentence, true, false.

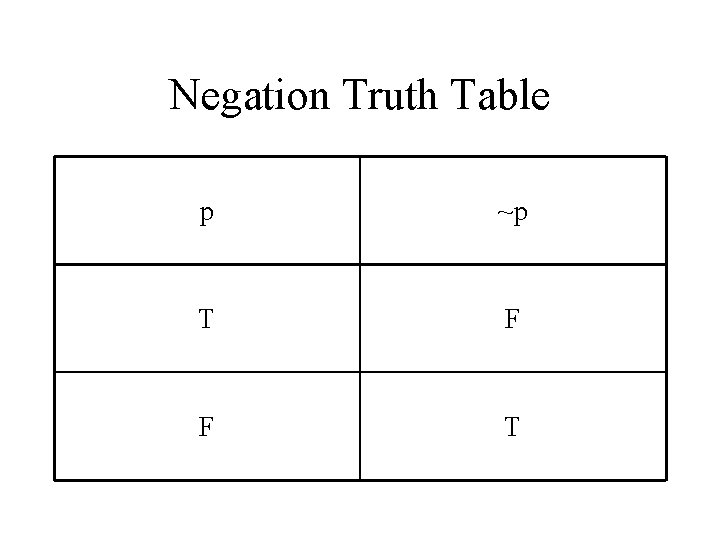
Logic Symbols ~ • ~ denotes “not” • Negation of p is ~p.

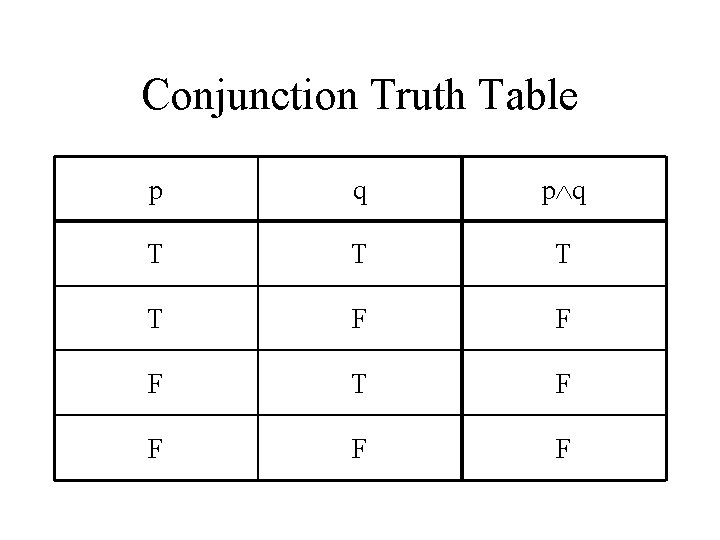
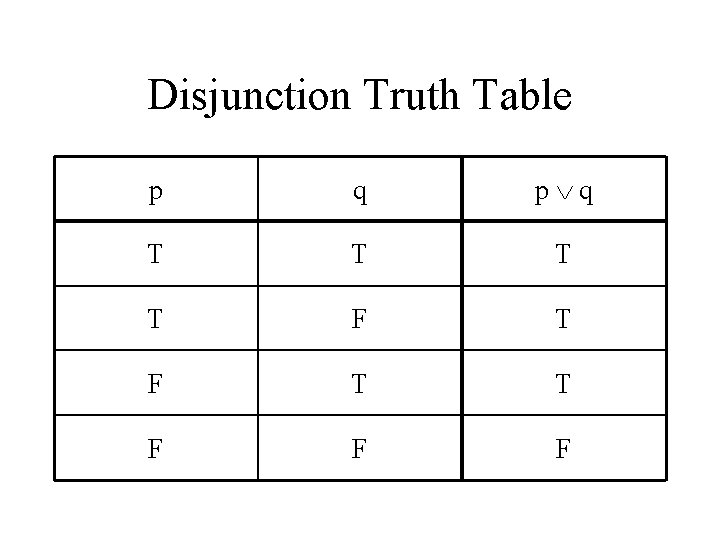
Logic Symbols ~ • • • denotes “and” Conjunction of p and q is p q. denotes “or” Disjunction of p and q is p q. Precedence: first ~ then and (unordered)

Truth Values • True • False

Precedence Examples • ~p q • ~p ~q • ~ (p q)
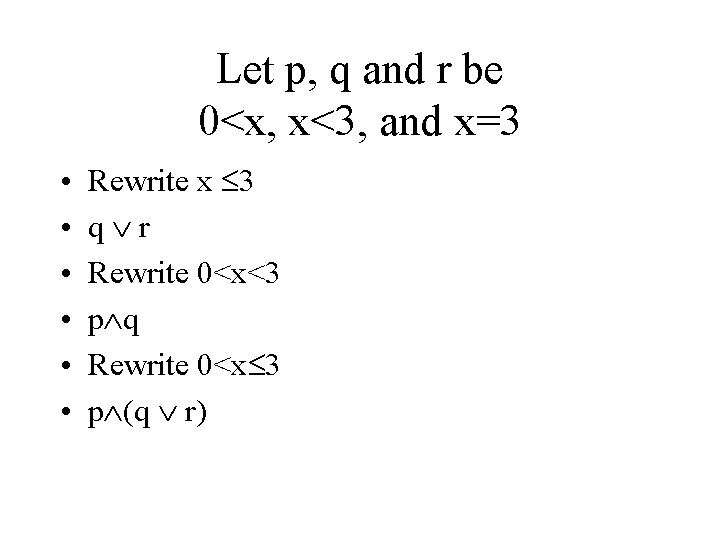
Let p, q and r be 0<x, x<3, and x=3 • • • Rewrite x 3 q r Rewrite 0<x<3 p q Rewrite 0<x 3 p (q r)

Negation Truth Table p ~p T F F T

Conjunction Truth Table p q T T F F F T F F

Disjunction Truth Table p q T T F F F

Statement Form • Statement variables • Logical connectives • Truth table

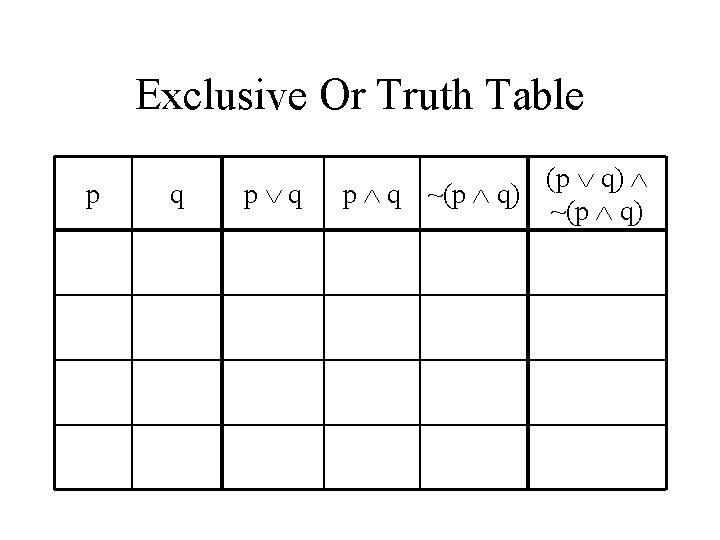
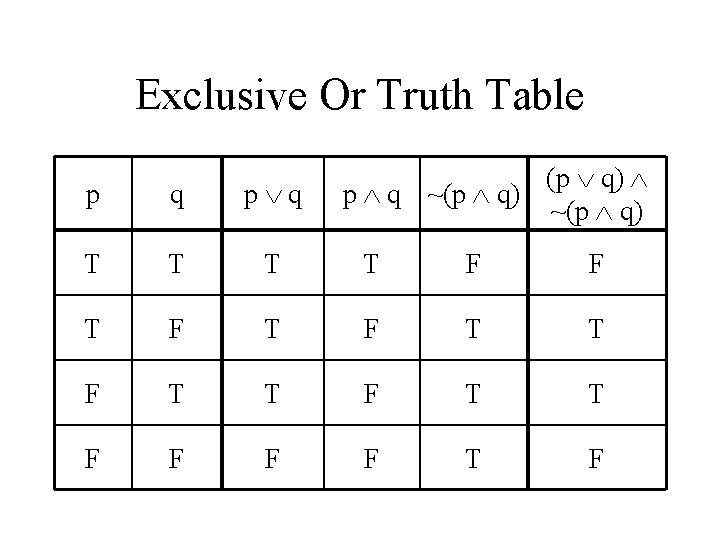
Exclusive Or • p or q but not both • (p q) ~(p q) • Do a truth table

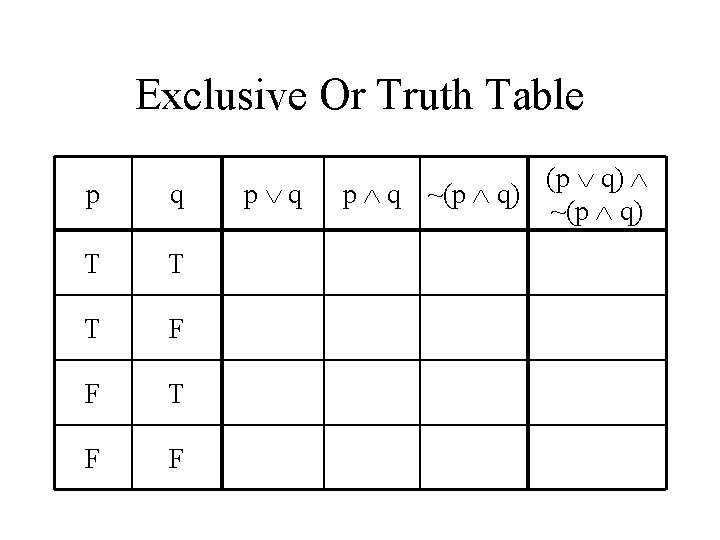
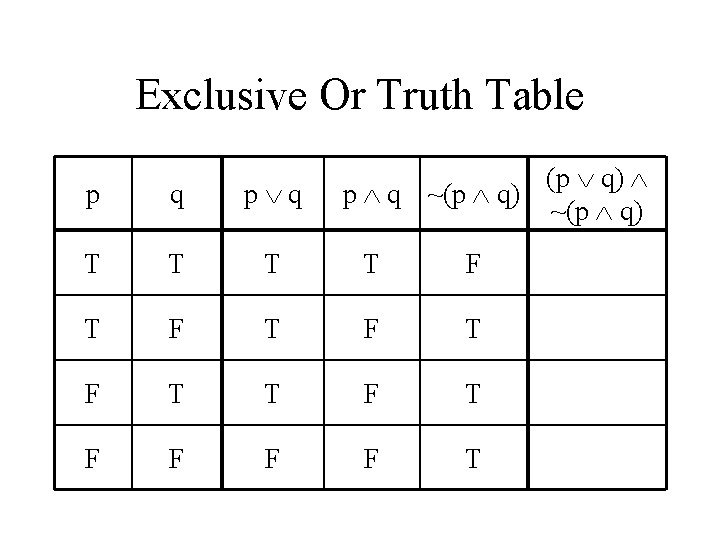
Exclusive Or Truth Table p q (p q) p q ~(p q)

Exclusive Or Truth Table p q T T T F F p q (p q) p q ~(p q)

Exclusive Or Truth Table (p q) p q ~(p q) p q T T F T F T T F F F F T

Exclusive Or Truth Table (p q) p q ~(p q) p q T T F F T F T T F F T F

Logical Equivalence • Statement Forms are logically equivalent if, and only if, they have the same truth tables. • P Q

Logical Equivalence Examples • 6>2 • p q • p 2<6 q p ~(~p)

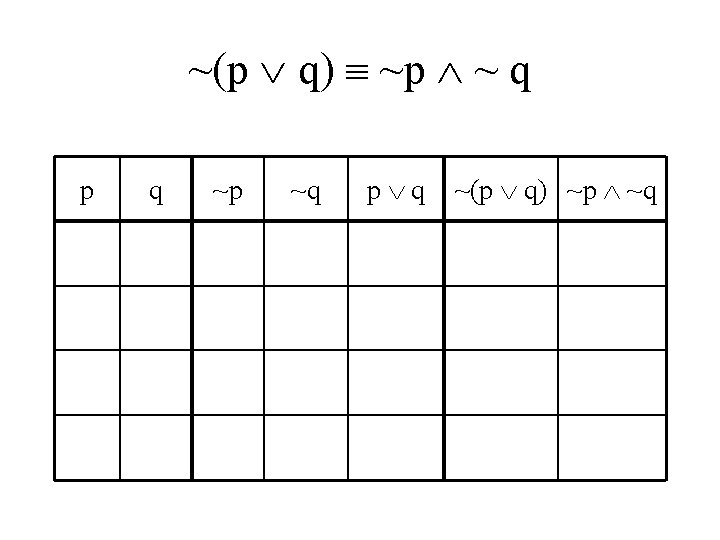
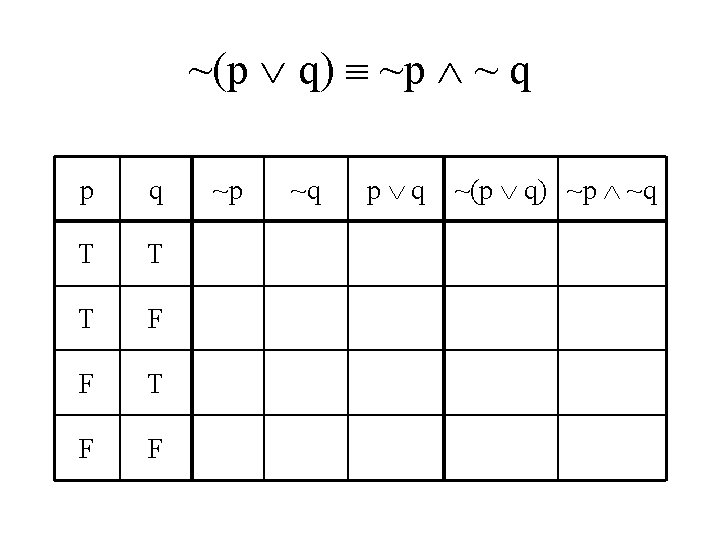
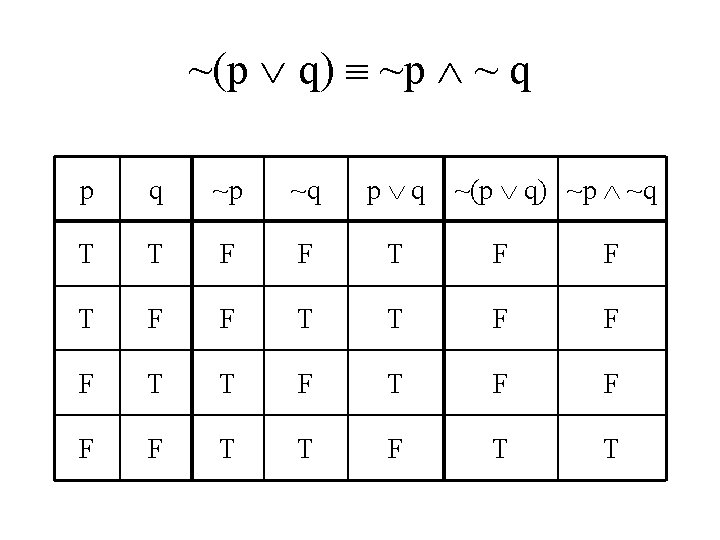
De Morgan’s Laws • ~(p q) ~p ~ q • Do truth tables

~(p q) ~p ~ q p q ~p ~q p q ~(p q) ~p ~q

~(p q) ~p ~ q p q T T T F F ~p ~q p q ~(p q) ~p ~q

~(p q) ~p ~ q p q ~p ~q p q ~(p q) ~p ~q T T F F T T F T F F T T

Practice Negations • John is six feet tall and weighs at least 200 pounds. • John is not six feet tall or he weighs less than 200 pounds.

Practice Negations • The bus was late or Tom’s watch was slow. • The bus was not late and Tom’s watch was not slow.

Jim is tall and thin. Logical And and Or are only allowed between statements.

Tautologies and Contradictions • A tautology is a statement form that is always true regardless of the values of the statement variables. • A contradiction is a statement form that is always false regardless of the values of the statement variables

Logically Equivalent Forms • • • Commutative laws Associative laws Distributive laws Identity laws Negation laws Double negative law • • • Idempotent laws De Morgan’s laws Universal bound laws Absorption laws Negations of tautologies and contradictions

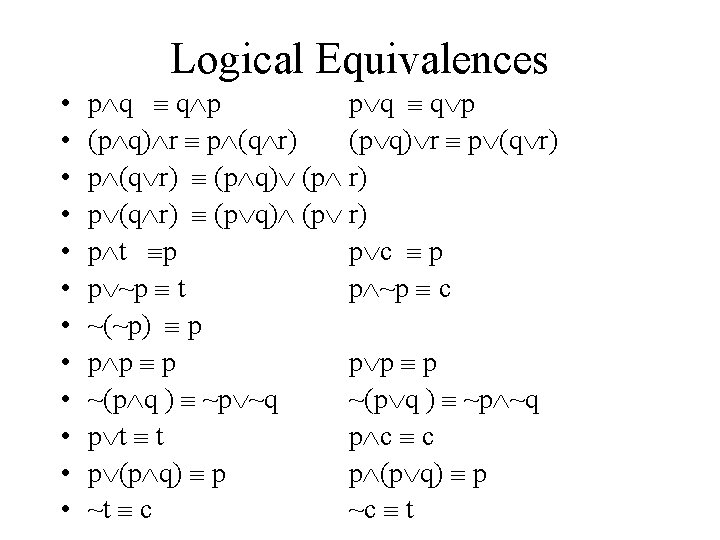
Logical Equivalences • • • p q q p (p q) r p (q r) (p q) (p r) p t p p c p p ~p t p ~p c ~(~p) p p p p ~(p q ) ~p ~q p t t p c c p (p q) p ~t c ~c t