Logical Effort sizing for speed EE 141 Digital









- Slides: 16

Logical Effort - sizing for speed © EE 141 Digital Integrated Circuits 2 nd 1 Combinational Circu

Sizing Logic Paths for Speed q Frequently, input capacitance of a logic path is constrained q Logic also has to drive some capacitance q Example: ALU load in an Intel’s microprocessor is 0. 5 p. F q How do we size the ALU datapath to achieve maximum speed? q We have already solved this for the inverter chain – can we generalize it for any type of logic? © EE 141 Digital Integrated Circuits 2 nd 2 Combinational Circu

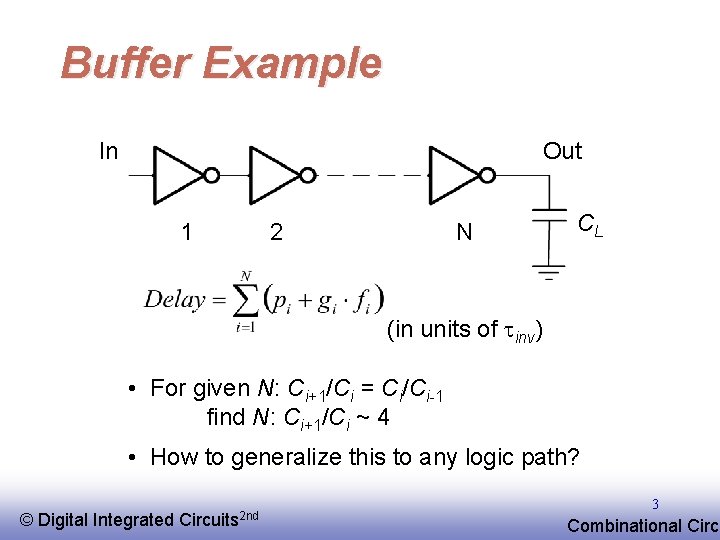
Buffer Example In Out 1 2 N CL (in units of tinv) • For given N: Ci+1/Ci = Ci/Ci-1 find N: Ci+1/Ci ~ 4 • How to generalize this to any logic path? © EE 141 Digital Integrated Circuits 2 nd 3 Combinational Circu

Logical Effort p – intrinsic delay (3 k. Runit. Cunitg) - gate parameter f(W) g – logical effort (k. Runit. Cunit) – gate parameter f(W) f – effective fanout (electrical effort) • Normalize everything to an inverter: ginv =1, pinv = 1 • Divide everything by tinv (everything is measured in unit delays tinv) • Assume g = 1. © EE 141 Digital Integrated Circuits 2 nd 4 Combinational Circu

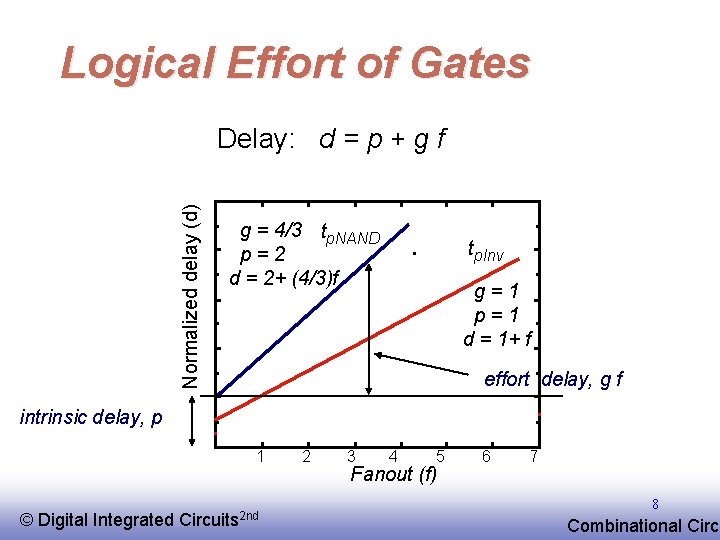
Delay in a Logic Gate • Gate delay: d=p+h intrinsic delay effort delay • Effort delay: h=gf logical effort electrical effort = effective fanout = Cout/Cin Logical effort is a function of topology, independent of sizing. Electrical effort (effective fanout) is a function of load/gate size © EE 141 Digital Integrated Circuits 2 nd 5 Combinational Circu

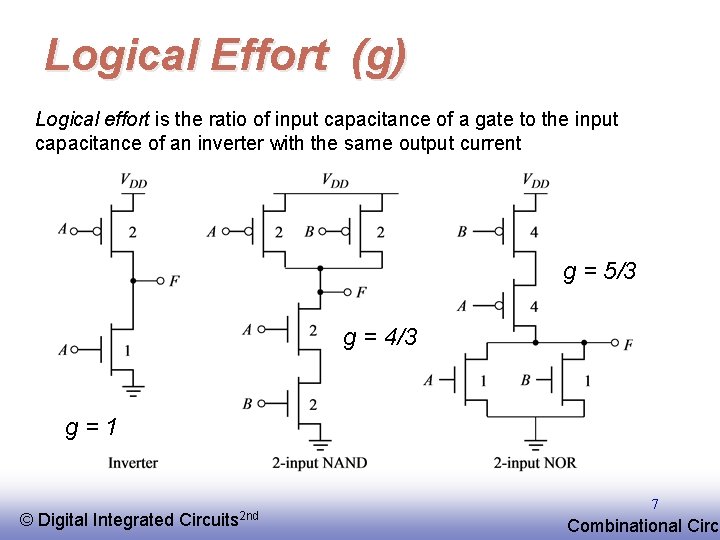
Logical Effort (g) q Inverter has the smallest logical effort and intrinsic delay of all static CMOS gates q Logical effort of a gate presents the ratio of its input capacitance to the inverter capacitance when sized to deliver the same current q Logical effort increases with the gate complexity © EE 141 Digital Integrated Circuits 2 nd 6 Combinational Circu

Logical Effort (g) Logical effort is the ratio of input capacitance of a gate to the input capacitance of an inverter with the same output current g = 5/3 g = 4/3 g=1 © EE 141 Digital Integrated Circuits 2 nd 7 Combinational Circu

Logical Effort of Gates Normalized delay (d) Delay: d = p + g f g = 4/3 tp. NAND p=2 d = 2+ (4/3)f tp. Inv g=1 p=1 d = 1+ f effort delay, g f intrinsic delay, p 1 © EE 141 Digital Integrated Circuits 2 nd 2 3 4 5 Fanout (f) 6 7 8 Combinational Circu

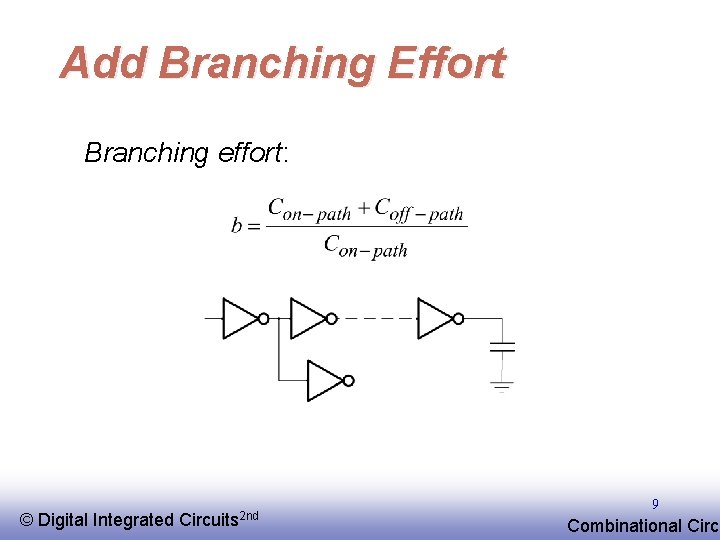
Add Branching Effort Branching effort: © EE 141 Digital Integrated Circuits 2 nd 9 Combinational Circu

Multistage Networks Stage effort: hi = gi fi • Path electrical effort: F = Cout/Cin • Path logical effort: G = g 1 g 2…g. N • Branching effort: B = b 1 b 2…b. N Total path effort: H = GFB Path delay D = Sdi = Spi + Shi © EE 141 Digital Integrated Circuits 2 nd 10 Combinational Circu

Optimum Effort per Stage Optimum delay is achieved when each stage bears the same effort: • Stage efforts: g 1 f 1 = g 2 f 2 = … = g. Nf. N • Effective fanout of each stage: • Minimum path delay © EE 141 Digital Integrated Circuits 2 nd 11 Combinational Circu

Optimal Number of Stages For a given load, and given input capacitance of the first gate, find optimum number of stages and optimal sizing Substitute ‘best stage effort’ © EE 141 Digital Integrated Circuits 2 nd 12 Combinational Circu

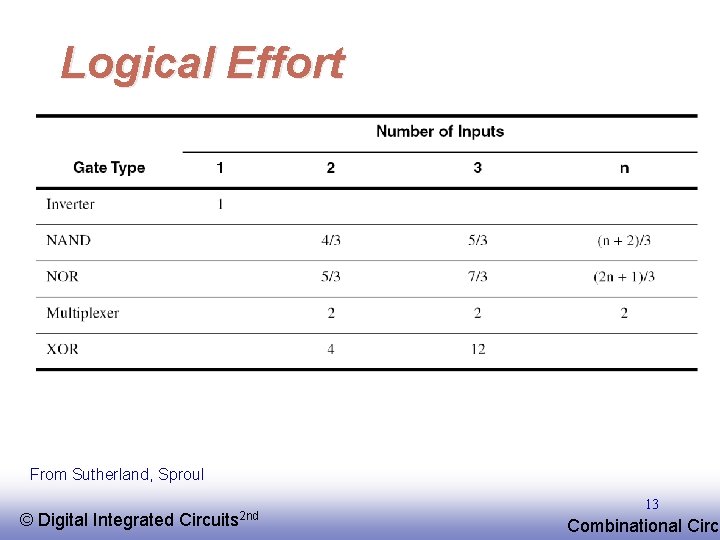
Logical Effort From Sutherland, Sproul © EE 141 Digital Integrated Circuits 2 nd 13 Combinational Circu

Method of Logical Effort q Compute the path effort: H = GFB q Find the optimum number of stages: N ~ log 4 H q Compute the stage effort h = H 1/N q Sketch the path with this number of stages q Work either from either end, find sizes (gate capacitance): Cin = Cout gi / h Cin or Cout = Cin h / gi Cout h / gi = f i Reference: Sutherland, Sproull, Harris, “Logical Effort, Morgan-Kaufmann 1999. © EE 141 Digital Integrated Circuits 2 nd 14 Combinational Circu

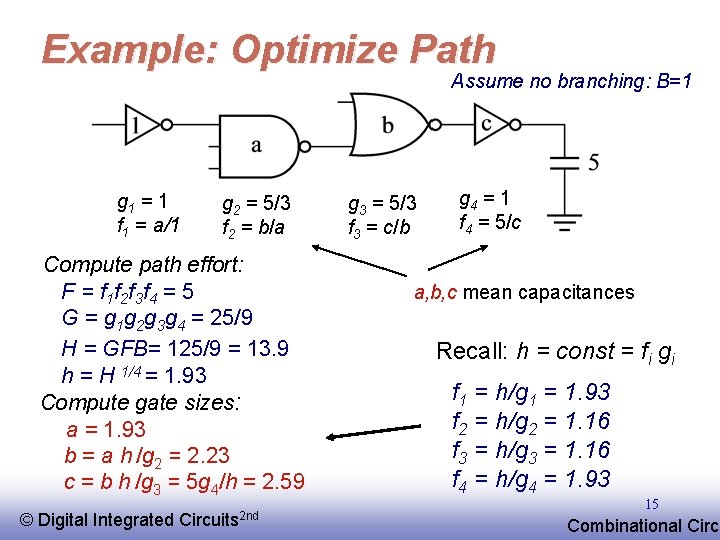
Example: Optimize Path Assume no branching: B=1 g 1 = 1 f 1 = a/1 g 2 = 5/3 f 2 = b/a Compute path effort: F = f 1 f 2 f 3 f 4 = 5 G = g 1 g 2 g 3 g 4 = 25/9 H = GFB= 125/9 = 13. 9 h = H 1/4 = 1. 93 Compute gate sizes: a = 1. 93 b = a h /g 2 = 2. 23 c = b h /g 3 = 5 g 4/h = 2. 59 © EE 141 Digital Integrated Circuits 2 nd g 3 = 5/3 f 3 = c/b g 4 = 1 f 4 = 5/c a, b, c mean capacitances Recall: h = const = fi gi f 1 = h/g 1 = 1. 93 f 2 = h/g 2 = 1. 16 f 3 = h/g 3 = 1. 16 f 4 = h/g 4 = 1. 93 15 Combinational Circu

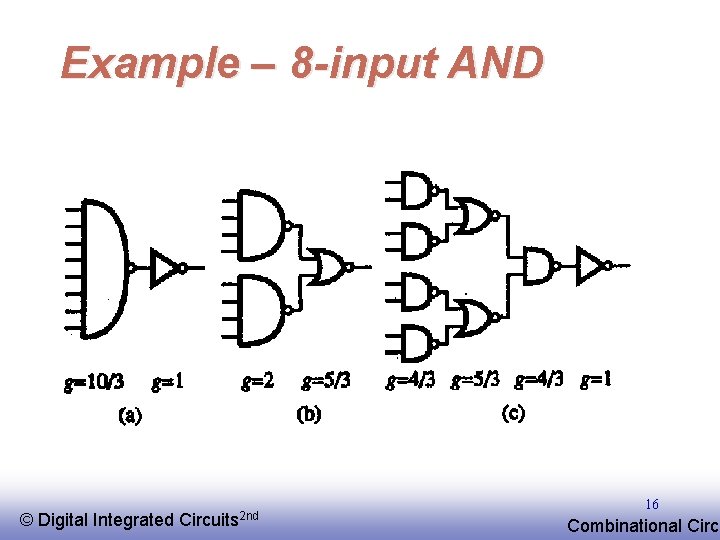
Example – 8 -input AND © EE 141 Digital Integrated Circuits 2 nd 16 Combinational Circu