Logical Clocks Topics Logical clocks l TotallyOrdered Multicasting

Logical Clocks

Topics Logical clocks l Totally-Ordered Multicasting l Vector timestamps l

Readings Van Steen and Tanenbaum: 5. 2 l Coulouris: 10. 4 l L. Lamport, “Time, Clocks and the Ordering of Events in Distributed Systems, ” Communications of the ACM, Vol. 21, No. 7, July 1978, pp. 558 -565. l C. J. Fidge, “Timestamps in Message-Passing Systems that Preserve the Partial Ordering”, Proceedings of the 11 th Australian Computer Science Conference, Brisbane, pp. 56 -66, February 1988. l

Ordering of Events For many applications, it is sufficient to be able to agree on the order that events occur and not the actual time of occurrence. l It is possible to use a logical clock to unambiguously order events l May be totally unrelated to real time. l Lamport showed this is possible (1978). l

The Happened-Before Relation l Lamport’s algorithm synchronizes logical clocks and is based on the happened-before relation: u l a b is read as “a happened before b” The definition of the happened-before relation: u u u If a and b are events in the same process and a occurs before b, then a b For any message m, send(m) rcv(m), where send(m) is the event of sending the message and rcv(m) is event of receiving it. If a, b and c are events such that a b and b c then a c

The Happened-Before Relation If two events, x and y, happen in different processes that do not exchange messages , then x y is not true, but neither is y x l The happened-before relation is sometimes referred to as causality. l

Example Say in process P 1 you have a code segment as follows: 1. 1 x = 5; 1. 2 y = 10*x; 1. 3 send(y, P 2); Say in process P 2 you have a code segment as follows: 2. 1 a=8; 2. 2 b=20*a; 2. 3 rcv(y, P 1); 2. 4 b = b+y; Let’s say that you start P 1 and P 2 at the same time. You know that 1. 1 occurs before 1. 2 which occurs before 1. 3; You know that 2. 1 occurs before 2. 2 which occurs before 2. 3 which is before 2. 4. You do not know if 1. 1 occurs before 2. 1 or if 2. 1 occurs before 1. 1. You do know that 1. 3 occurs before 2. 3 and 2. 4

Example l Continuing from the example on the previous page – The order of actual occurrence of operations is often not consistent from execution to execution. For example: u u u l l Execution 1 (order of occurrence): 1. 1, 1. 2, 1. 3, 2. 1, 2. 2, 2. 3, 2. 4 Execution 2 (order of occurrence): 2. 1, 2. 2, 1. 1, 1. 2, 1. 3, 2. 4 Execution 3 (order of occurrence) 1. 1, 2. 2, 1. 3, 2. 4 We can say that 1. 1 “happens before” 2. 3, but not that 1. 1 “happens before” 2. 2 or that 2. 2 “happens before” 1. 1. Note that the above executions provide the same result.

Lamport’s Algorithm l We need a way of measuring time such that for every event a, we can assign it a time value C(a) on which all processes agree on the following: u u The clock time C must monotonically increase i. e. , always go forward. If a b then C(a) < C(b) Each process, p, maintains a local counter Cp l The counter is adjusted based on the rules presented on the next page. l

Lamport’s Algorithm 1. 2. 3. Cp is incremented before each event is issued at process p: Cp = Cp + 1 When p sends a message m, it piggybacks on m the value t=Cp On receiving (m, t), process q computes Cq = max(Cq, t) and then applies the first rule before timestamping the event rcv(m).

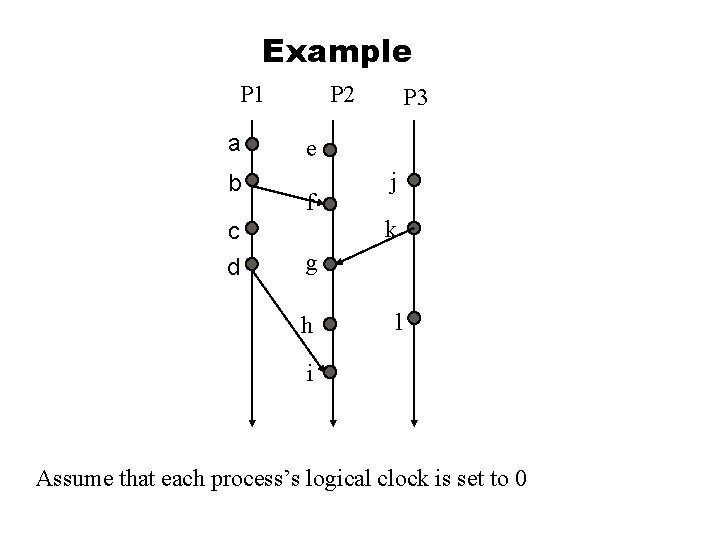
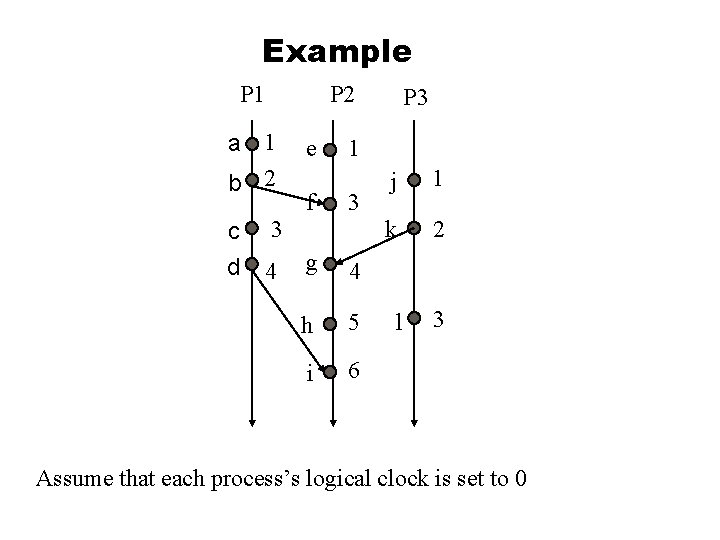
Example P 1 a b c d P 2 P 3 e f j k g h l i Assume that each process’s logical clock is set to 0

Example P 1 P 2 a 1 b 2 c d e f 1 3 3 4 P 3 g 4 h 5 i 6 j 1 k 2 l 3 Assume that each process’s logical clock is set to 0

Example l From the timing diagram on the previous slide, what can you say about the following events? Between a and b: a b u Between b and f: b f u Between e and k: concurrent u Between c and h: concurrent u Between k and h: k h u

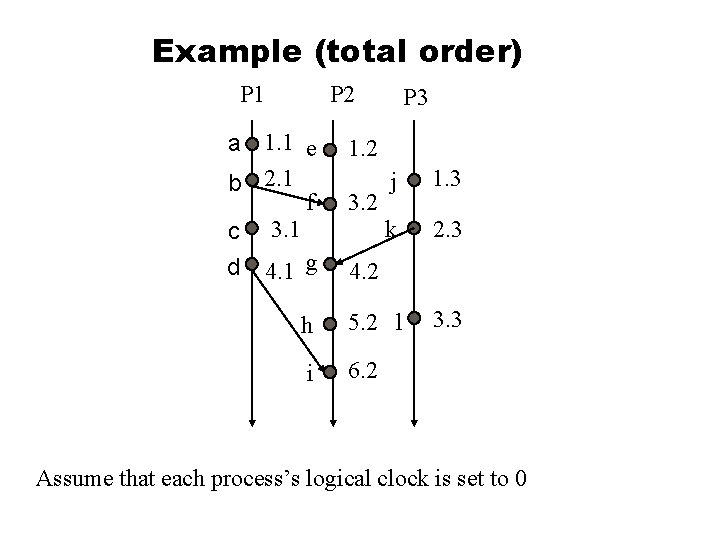
Total Order A timestamp of 1 is associated with events a, e, j in processes P 1, P 2, P 3 respectively. l A timestamp of 2 is associated with events b, k in processes P 1, P 3 respectively. l The times may be the same but the events are distinct. l We would like to create a total order of all events i. e. for an event a, b we would like to say that either a b or b a l

Total Order Create total order by attaching a process number to an event. l Pi timestamps event e with Ci (e). i l We then say that Ci(a). i happens before Cj(b). j iff: l Ci(a) < Cj(b); or u Ci(a) = Cj(b) and i < j u

Example (total order) P 1 P 2 a 1. 1 e b 2. 1 f c 3. 1 d 4. 1 g P 3 1. 2 j 1. 3 k 2. 3 h 5. 2 l 3. 3 i 6. 2 3. 2 4. 2 Assume that each process’s logical clock is set to 0

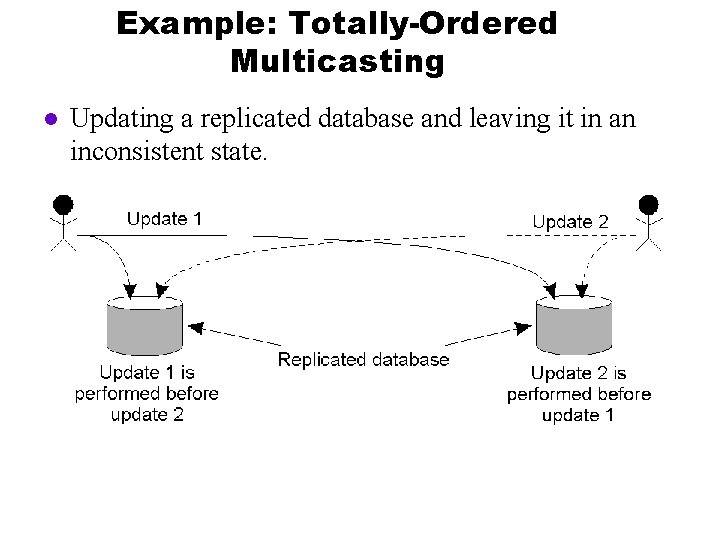
Example: Totally-Ordered Multicast l l Application of Lamport timestamps (with total order) Scenario Replicated accounts in New York(NY) and San Francisco(SF) u Two transactions occur at the same time and multicast n Current balance: $1, 000 n Add $100 at SF n Add interest of 1% at NY n If not done in the same order at each site then one site will record a total amount of $1, 111 and the other records $1, 110. u

Example: Totally-Ordered Multicasting l Updating a replicated database and leaving it in an inconsistent state.

Example: Totally-Ordered Multicasting l l l We must ensure that the two update operations are performed in the same order at each copy. Although it makes a difference whether the deposit is processed before the interest update or the other way around, it does matter which order is followed from the point of view of consistency. We need totally-ordered multicast, that is a multicast operation by which all messages are delivered in the same order to each receiver. u NOTE: Multicast refers to the sender sending a message to a collection of receivers.

Example: Totally Ordered Multicast l Algorithm Update message is timestamped with sender’s logical time u Update message is multicast (including sender itself) u When message is received n It is put into local queue n Ordered according to timestamp, n Multicast acknowledgement u

Example: Totally Ordered Multicast l Message is delivered to applications only when It is at head of queue u It has been acknowledged by all involved processes u Pi sends an acknowledgement to Pj if n P has not made an update request i n P ’s identifier is greater than P ’s identifier i j n P ’s update has been processed; i u l Lamport algorithm (extended for total order) ensures total ordering of events

Example: Totally Ordered Multicast On the next slide m corresponds to “Add $100” and n corresponds to “Add interest of 1%”. l When sending an update message (e. g. , m, n) the message will include the timestamp generated when the update was issued. l

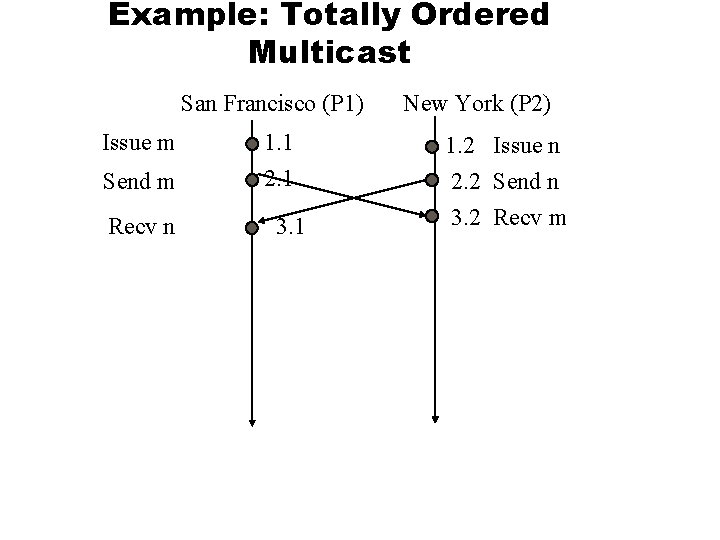
Example: Totally Ordered Multicast San Francisco (P 1) Issue m 1. 1 Send m 2. 1 Recv n 3. 1 New York (P 2) 1. 2 Issue n 2. 2 Send n 3. 2 Recv m

Example: Totally Ordered Multicast l l l The sending of message m consists of sending the update operation and the time of issue which is 1. 1 The sending of message n consists of sending the update operation and the time of issue which is 1. 2 Messages are multicast to all processes in the group including itself. u u Assume that a message sent by a process to itself is received by the process almost immediately. For other processes, there may be a delay.

Example: Totally Ordered Multicast l At this point, the queues have the following: u u l P 1 will multicast an acknowledgement for (m, 1. 1) but not (n, 1. 2). u u l P 1: (m, 1. 1), (n, 1. 2) P 2: (m, 1. 1), (n, 1. 2) Why? P 1’s identifier is higher then P 2’s identifier and P 1 has issued a request 1. 1 < 1. 2 P 2 will multicast an acknowledgement for (m, 1. 1) and (n, 1. 2) u u Why? P 2’s identifier is not higher then P 1’s identifier 1. 1 < 1. 2

Example: Totally Ordered Multicast l P 1 does not issue an acknowledgement for (n, 1. 2) until operation m has been processed. u 1< 2 Note: The actual receiving by P 1 of message (n, 1. 2) is assigned a timestamp of 3. 1. l Note: The actual receiving by P 2 of message (m, 1. 1) is assigned a timestamp of 3. 2 l

Example: Totally Ordered Multicast l If P 2 gets (n, 1. 2) before (m, 1. 1) does it still multicast an acknowledgement for (n, 1. 2)? u l At this point, how does P 2 know that there are other updates that should be done ahead of the one it issued? u u l Yes! It doesn’t; It does not proceed to do the update specified in (n, 1. 2) until it gets an acknowledgement from all other processes which in this case means P 1. Does P 2 multicast an acknowledgement for (m, 1. 1) when it receives it? u Yes, it does since 1 < 2

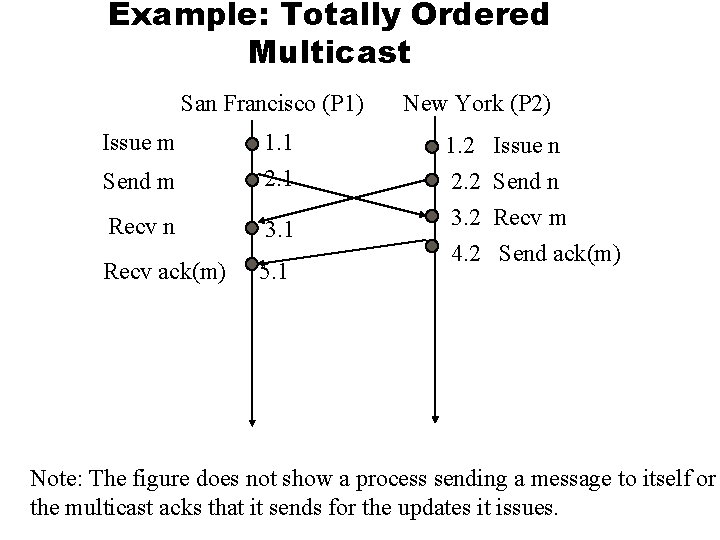
Example: Totally Ordered Multicast San Francisco (P 1) Issue m 1. 1 Send m 2. 1 Recv n 3. 1 Recv ack(m) 5. 1 New York (P 2) 1. 2 2. 2 3. 2 4. 2 Issue n Send n Recv m Send ack(m) Note: The figure does not show a process sending a message to itself or the multicast acks that it sends for the updates it issues.

Example: Totally Ordered Multicast l To summarize, the following messages have been sent: P 1 and P 2 have issued update operations. u P 1 has multicasted an acknowledgement message for (m, 1. 1). u P 2 has multicasted acknowledgement messages for (m, 1. 1), (n, 1. 2). u P 1 and P 2 have received an acknowledgement message from all processes for (m, 1. 1). l Hence, the update represented by m can proceed in both P 1 and P 2. l

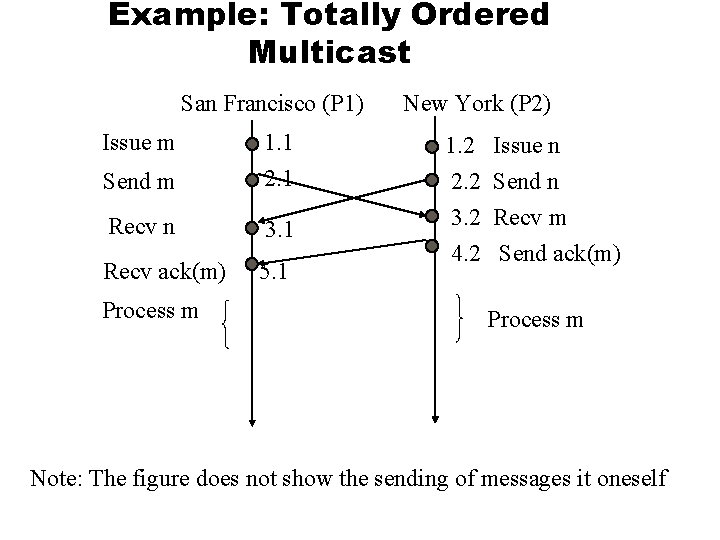
Example: Totally Ordered Multicast San Francisco (P 1) Issue m 1. 1 Send m 2. 1 Recv n 3. 1 Recv ack(m) 5. 1 Process m New York (P 2) 1. 2 2. 2 3. 2 4. 2 Issue n Send n Recv m Send ack(m) Process m Note: The figure does not show the sending of messages it oneself

Example: Totally Ordered Multicast When P 1 has finished with m, it can then proceed to multicast an acknowledgement for (n, 1. 2). l When P 1 and P 2 both have received this acknowledgement, then it is the case that acknowledgements from all processes have been received for (n, 1. 2). l At this point, it is known that the update represented by n can proceed in both P 1 and P 2. l

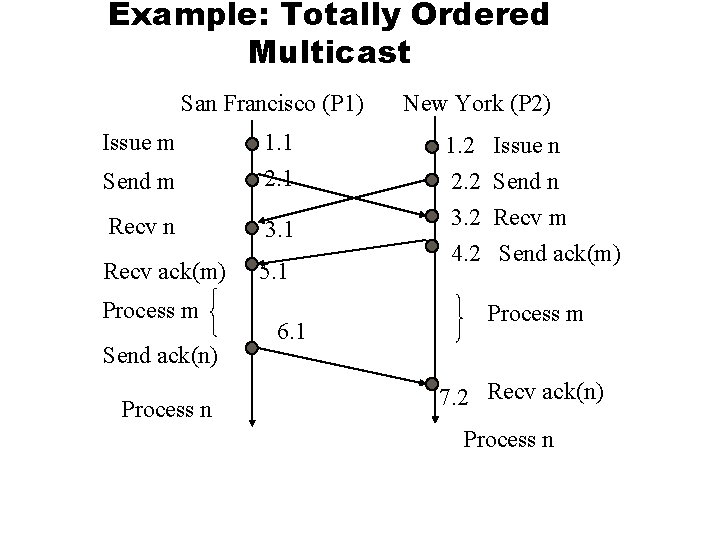
Example: Totally Ordered Multicast San Francisco (P 1) Issue m 1. 1 Send m 2. 1 Recv n 3. 1 Recv ack(m) 5. 1 Process m Send ack(n) Process n 6. 1 New York (P 2) 1. 2 2. 2 3. 2 4. 2 Issue n Send n Recv m Send ack(m) Process m 7. 2 Recv ack(n) Process n

Example: Totally Ordered Multicast l l What if there was a third process e. g. , P 3 that issued an update (call it o) at about the same time as P 1 and P 2. The algorithm works as before. u u l P 1 will not multicast an acknowledgement for o until m has been done. P 2 will not multicast an acknowledgement for o until n has been done. Since an operation can’t proceed until acknowledgements for all processes have been received, o will not proceed until n and m have finished.

Problems with Lamport Clocks Lamport timestamps do not capture causality. l With Lamport’s clocks, one cannot directly compare the timestamps of two events to determine their precedence relationship. l If C(a) < C(b) is not true then a b is also not true. u Knowing that C(a) < C(b) is true does not allow us to conclude that a b is true. u Example: In the first timing diagram, C(e) = 1 and C(b) = 2; thus C(e) < C(b) but it is not the case that e b u

Problem with Lamport Clocks The main problem is that a simple integer clock cannot order both events within a process and events in different processes. l C. Fidge developed an algorithm that overcomes this problem. l Fidge’s clock is represented as a vector [v 1, v 2, …, vn] with an integer clock value for each process (vi contains the clock value of process i). This is a vector timestamp. l

Fidge’s Algorithm Properties of vector timestamps l vi [i] is the number of events that have occurred so far at Pi l If vi [j] = k then Pi knows that k events have occurred at Pj l

Fidge’s Algorithm l The Fidge’s logical clock is maintained as follows: 1. 2. 3. 4. Initially all clock values are set to the smallest value (e. g. , 0). The local clock value is incremented at least once before each primitive event in a process i. e. , vi[i] = vi[i] +1 The current value of the entire logical clock vector is delivered to the receiver for every outgoing message. Values in the timestamp vectors are never decremented.

Fidge’s Algorithm 5. u Upon receiving a message, the receiver sets the value of each entry in its local timestamp vector to the maximum of the two corresponding values in the local vector and in the remote vector received. Let vq be piggybacked on the message sent by process q to process p; We then have: n For i = 1 to n do vp[i] = max(vp[i], vq [i] ); vp[p] = vp[p] + 1;

Fidge’s Algorithm l For two vector timestamps, va and vb va is not equal to vb if there exists an i such that va[i] is not equal to vb[i] u va <= vb if for all i va[i] <= vb[i] u va < vb if for all i va[i] < = vb[i] AND va is not equal to vb u l Events a and b are causally related if va < vb or vb< va.

Example P 2 P 1 [1, 0, 0] a [2, 0, 0] b [3, 0, 0] c [4, 0, 0] d P 3 [0, 1, 0] e f [2, 2, 0] j [0, 0, 1] k [0, 0, 2] l [0, 0, 3] [2, 3, 2] g h [2, 4, 2] i [4, 5, 2]

Vector Timestamps and Causality l l l We have looked at total order of messages where all messages are processed in the same order at each process. It is possible to have any order where all you care about is that a message reaches all processes, but you don’t care about the order of execution. Causal order is used when a message received by a process can potentially affect any subsequent message sent by that process. Those messages should be received in that order at all processes. Unrelated messages may be delivered in any order.

Causality and Modified Vector Timestamps With a slight adjustment, vector timestamps can be used to guarantee causal message delivery. l We will illustrate this adjustment, the definition of causality and the motivation through an example. l

Example Application: Bulletin Board The Internet’s electronic bulletin board service (network news) l Users (processes) join specific groups (discussion groups). l Postings, whether they are articles or reactions, are multicast to all group members. l Could use a totally-ordered multicasting scheme. l

Display from a Bulletin Board Program l l Users run bulletin board applications which multicast messages One multicast group per topic (e. g. os. interesting) Require reliable multicast - so that all members receive messages Ordering: Bulletin board: os. interesting total (makes the numbers the same at all sites) Item From Subject 23 A. Hanlon Mach 24 G. Joseph Microkernels 25 A. Hanlon Re: Microkernels 26 T. L’Heureux RPC performance 27 M. Walker Re: Mach end FIFO (gives sender order) causal (makes replies come after original message) Figure 11. 13 Colouris •

Example Application: Bulletin Board A totally-ordered multicasting scheme does not imply that if message B is delivered after message A, that B is a reaction to A. l Totally-ordered multicasting is too strong in this case. l The receipt of an article causally precedes the posting of a reaction. The receipt of the reaction to an article should always follow the receipt of the article. l

Example Application: Bulletin Board If we look at the bulletin board example, it is allowed to have items 26 and 27 in different order at different sites. l Items 25 and 26 may be in different order at different sites. l

Example Application: Bulletin Board Vector timestamps can be used to guarantee causal message delivery. A slight variation of Fidge’s algorithm is used. l Each process Pi has an array Vi where Vi[j] denotes the number of events that process Pi knows have taken place. l

Example Application: Bulletin Board l l Vector timestamps are assumed to be updated only when posting or receiving articles i. e. , when a message is sent or received. Let Vq be piggybacked on the message sent by process q to process p; When p receives the message, then p does the following: n For i = 1 to n do Vp[i] l = max(Vp[i], Vq [i] ); When p sends a message, it does the following: Vp[p] = Vp[p] + 1;

Example Application: Bulletin Board When a process Pi posts an article, it multicasts that article as a message with the vector timestamp. Let’s call this message a. Assume that the value of the timestamp is Vi l Process Pj posts a reaction. Let’s call this message r. Assume that the value of the timestamp is Vj l Note that Vj > Vi l Message r may arrive at Pk before message a. l

Example Application: Bulletin Board Pk will postpone delivery of r to the display of the bulletin board until all messages that causally precede r have been received as well. l Message r is delivered iff the following conditions are met: l Vj[j] = Vk[j]+1 n This states that r is the next message that P was k expecting from process Pj u Vj[i] <= Vk[i] for all i not equal to j n This states that P has seen at least as many messages as k seen by Pj when it sent message r. u

Example Application: Bulletin Board l l Initially Vj[i] = 0 and Vk[i] =0 for all i. This makes sense since no messages have been sent. Let’s say that Pj sends a message where Vj[j] = 1. This implies that this is the first message sent by Pj Since Vk[j] is 0 then it will accept the message sent by Pj since it is expecting a first message from Pj. Let’s say that Pj sent a message where Vj[j] = 5 (indicating a 5 th message sent) and that Vk[j] is 3 which indicates Pk is expecting the 4 th message sent by Pj. This indicates that the received message should be held back.

Example Application: Bulletin Board Assume that Vj[i] <= Vk[i] is not true for some i. In other words, Vj[i] > Vk[i] for some i. This indicates that Pi sent a message that was received by Pj but not Pk. l In this case Pk will not deliver this message until it gets the missing message. l

Example Application: Bulletin Board P 2 [0, 0, 0] P 1 [0, 0, 0] P 3 [0, 0, 0] Post a [1, 0, 0] a c [1, 0, 0] e [1, 0, 0] [1, 0, 1] r: Reply a b d [1, 0, 1] g [1, 0, 1] Message a arrives at P 2 before the reply r from P 3 does

Example Application: Bulletin Board P 2 [0, 0, 0] P 1 [0, 0, 0] P 3 [0, 0, 0] Post a [1, 0, 0] g [1, 0, 1] r: Reply a Buffered b [1, 0, 1] d c [1, 0, 0] Deliver r The message a arrives at P 2 after the reply from P 3; The reply is not delivered right away.

Summary No notion of a globally shared clock. l Local (physical) clocks must be synchronized based on algorithms that take into account network latency. l Knowing the absolute time is not necessary. l Logical clocks can be used for ordering purposes. l