LOGICA CLASICA DE PRIMER ORDEN Jos Alfredo Amor
























![Ejemplos de Fórmulas de LP • x [P(x, c) y P(y, c)] x[(P(x) Q(x)) Ejemplos de Fórmulas de LP • x [P(x, c) y P(y, c)] x[(P(x) Q(x))](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-25.jpg)






![Cuantificación Existencial • [ x Q(x)] es verdadera respecto a la interpretación dada, si Cuantificación Existencial • [ x Q(x)] es verdadera respecto a la interpretación dada, si](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-32.jpg)
![Cuantificación Universal • [ x Q(x)] es verdadera respecto a la interpretación dada, si Cuantificación Universal • [ x Q(x)] es verdadera respecto a la interpretación dada, si](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-33.jpg)




![Un último ejemplo • x y [ R(x, y) R(y, y) ] • “No Un último ejemplo • x y [ R(x, y) R(y, y) ] • “No](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-38.jpg)












































































- Slides: 114

LOGICA CLASICA DE PRIMER ORDEN José Alfredo Amor jaam@hp. fciencias. unam. mx • • • Resumen La lógica clásica de primer orden con igualdad es la rama más estudiada, aplicada y conocida de la lógica contemporánea. Desde luego, presuponemos que la lógica proposicional o lógica de enunciados, forma parte de la lógica de primer orden. La razón de esto es su riqueza expresiva, su versatilidad y aplicabilidad, sus teoremas fundamentales, así como su uso de modo importante en matemáticas, filosofía de la ciencia, ciencias de la computación y el razonamiento automático. Esto último ha tenido un desarrollo espectacular en la segunda mitad del siglo pasado. Por otro lado, la lógica clásica ha sido el punto obligado de referencia y comparación para la gran cantidad de lógicas no clásicas que se han desarrollado en ese siglo. El razonamiento deductivo clásico es el proceso de obtener conclusiones a partir de suposiciones o hechos; esas conclusiones se conocen como consecuencias lógicas de las suposiciones o hechos. El razonamiento deductivo correcto es el razonamiento deductivo en el que las conclusiones se siguen necesaria e inevitablemente de las suposiciones o hechos. Podemos pensar a la lógica clásica como el estudio del razonamiento deductivo correcto. El objetivo fundamental de la lógica en general es explicar la noción de consecuencia lógica la cual es una relación que se da entre un conjunto de enunciados (llamados premisas) y un enunciado particular (llamado conclusión). Dicho concepto de consecuencia lógica, en el caso de la lógica clásica de primer orden con igualdad, representa con rigor matemático la idea intuitiva de inferencia válida o inferencia correcta. Para lograr este objetivo, la lógica clásica de primer orden con igualdad utiliza, al igual que muchas otras lógicas, un lenguaje formal propio, definido de un modo riguroso al estilo matemático, basado en formas y no en significados. Los lenguajes formales son muy diferentes a los lenguajes naturales, por ejemplo sus símbolos forman oraciones de un modo absolutamente preciso, lo que evita ambigüedades como las de los lenguajes naturales y su interpretación está definida también de un modo riguroso por lo que los conceptos de verdadero o falso quedan definidos también de modo preciso.

Lógica de Predicados o Lógica de Primer Orden o Lógica Cuantificacional José Alfredo Amor Facultad de Ciencias UNAM jaam@hp. fciencias. unam. mx Abril de 2005

En el lenguaje coloquial se llama “lógico” a lo que es considerado de sentido común ¿Este sentido común que aplicamos en situaciones reales debe dirigir la construcción del razonamiento lógico? o por el contrario, ¿Son las normas de la lógica las que deben regir nuestra manera natural de razonar?

Es decir: ¿La manera natural de razonar determina a la lógica, o la lógica nos enseña a razonar correctamente? ¿Qué es lo lógico y lo no lógico?

¿Esto es lógico o no lógico ?

¿Esto es lógico o no lógico ?

LA LÓGICA • Podemos pensar a la lógica clásica como el estudio del razonamiento deductivo correcto. • El razonamiento deductivo correcto es el proceso de obtener conclusiones a partir de suposiciones o hechos, en el que las conclusiones se siguen necesariamente de las suposiciones o hechos.

• Esto es sumamente importante en matemáticas, ya que las pruebas en matemáticas son sucesiones de argumentos, y estos deben ser argumentos correctos. Resulta pues obvia la importancia de saber si un argumento dado es correcto o no.

DIPLOMADO EN LOGICA Módulo: Lógica de Predicados I. LA LOGICA DE PREDICADOS (o cuantificacional o de primer orden) • II. SEMÁNTICA DE LA LÓGICA DE PRIMER ORDEN • III. SINTAXIS DE LA LÓGICA DE PRIMER ORDEN • IV. LOGICA DE PRIMER ORDEN ENFOQUE COMPUTACIONAL

I. LA LOGICA DE PREDICADOS (O CUANTIFICACIONAL O DE PRIMER ORDEN) 1. Lenguajes naturales y lenguaje analítico. 2. Traducciones del lenguaje natural al lenguaje analítico, e inversamente. 3. Relación entre la lógica proposicional y la lógica cuantificacional. 4. Reglas de formación de fórmulas. Variables, enunciados. La igualdad.

II. LA SEMÁNTICA DE LA LÓGICA DE PRIMER ORDEN 1. Prerrequisitos de teoría de conjuntos. 2. Interpretaciones: verdad o falsedad de enunciados respecto a una interpretación. 3. Definición de verdad de Tarski. Fórmulas lógicamente válidas. 4. Argumentos deductivos válidos e inválidos. 5. La igualdad. Fórmulas y argumentos que incluyen igualdades.

III. LA SINTAXIS DE LA LÓGICA DE PRIMER ORDEN • 1. Deducción natural. Solo reglas. Correctud y Completud. • 2. Sistemas axiomáticos: axiomas, reglas de inferencia y definición de deducción. Metateorema de la Deducción. Correctud y Completud. • 3. Otros conceptos relacionados: teorías, consistencia, satisfacibilidad, completud, axiomatizabilidad, decidibilidad, etc.

IV. LOGICA DE PRIMER ORDEN ENFOQUE COMPUTACIONAL • 1. Regla de RESOLUCION. Correctud y Completud • 2. Demostración Automática de Teoremas • 3. Programación Lógica

Enunciados simples • • Paris es la Capital de Francia 2 + 2 = 1 El Sol es una estrella Vincente Fox es el presidente de México en el año 2005 • La UNAM tiene más de 250 mil estudiantes

Enunciados simples • • Paris es la Capital de Francia C(p, f) 2 + 2 = 1 =(2+2, 1) El Sol es una estrella E(s) Vincente Fox es el presidente de México en el año 2005 PM(f, 2005) • La UNAM tiene más de 250 mil estudiantes est(u)>250 mil

Enunciados complejos • Tegucigalpa es la capital de algún país y alguna ciudad es la capital de Costa Rica • Caracas es la capital de Venezuela y San José es la capital de Costa Rica • Si 2+2 = 4 y 4 es par, entonces 2+2 es par • No existe alguien que rasure a todos los que no se rasuran a si mismos y sólo a esos

CUANTIFICADORES Y VARIABLES • El uso de cuantificadores y variables no es común en el lenguaje coloquial. • Pero cuando se comprende su poder expresivo y riguroso se ha dado el primer paso para saber expresarse con él.

Lenguaje formal LP: símbolos básicos • Parámetros de predicado: letras mayúsculas del alfabeto P, Q, R, …. • Parámetros de constante: letras minúsculas a, b, c, …. • Variables individuales: x, y, z, w, …. • Símbolos lógicos: , , , = • Símbolos de cuantificación: , • Símbolos auxiliares: ), (

Reglas de construcción de fórmulas de LP *Todo parámetro de predicado aplicado a constantes o variables y toda igualdad de constantes o variables, es una fórmula (atómica) de LP *Si y son fórmulas de LP, entonces ( ), ( ) y ( ) son fórmulas de LP *Si es una fórmula de LP y x es una variable entonces ( x ) y ( x ), son fórmulas de LP

Formalizar el Lenguaje Coloquial • No se pretende formalizar todo el lenguaje coloquial sino el de contenido preciso estilo matemático: “Todo S es P" y “Algún S es P” • x[S(x) P(x)] y x [S(x) P(x)] S(x) simboliza “x es S” y P(x) “x es P” Estas expresiones son nuevas para el alumno por eso hay dificultad para representarlas

Proposiciones Categóricas en LP UNIVERSAL AFIRMATIVA NEGATIVA • A: Todo S es P E: Ningún S es P • x [S(x) P(x)] x [S(x) P(x)] PARTICULAR AFIRMATIVA NEGATIVA • I: Algún S es P O: Algún S no es P • x [S(x) P(x)]

EXPRESIVIDAD DEL LENGUAJE LP (PERROS Y CARTEROS) 1. Todos los perros muerden a algún cartero • x[P(x) y(C(y) M(x, y))] 2. Hay un cartero al que muerden todos los perros • x[C(x) y( P(y) M(y, x)] 3. Todos los carteros son mordidos poralgún perro • x[C(x) y (P(y) / M(y, x)] 4. Hay un perro que muerde a todos los carteros • x [P(x) / y(C(y) M(x, y)]

Y SE PUEDE COMPLICAR! Todos los perros que asustan a algún cartero, lo muerden: x y [P(x) / C(y) / A(x, y) M(x, y)] o bien: x[P(x) y(C(y) / A(x, y) M(x, y))] Hay un perro que muerde a todos los perros que muerden a algún cartero: • x[P(x) / y(P(y) / z(C(z) / M(y, z)) M(x, y))]

Ejemplos Fórmulas de LP • Todos son amigos de alguien: x y A(x, y) • Todos son amigos de todos: x y A(x, y) • Juan vió a María con el telescopio: VT(j, m) ? V(j, m) T(m) ? • Alguien es amigo de todos: x y A (x, y)
![Ejemplos de Fórmulas de LP x Px c y Py c xPx Qx Ejemplos de Fórmulas de LP • x [P(x, c) y P(y, c)] x[(P(x) Q(x))](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-25.jpg)
Ejemplos de Fórmulas de LP • x [P(x, c) y P(y, c)] x[(P(x) Q(x)) ( Q(x) P(x))] • x [P(x) y (P(y) x = y)] • [ x P(x)] x y[P(x) P(y) x = y]

CRITERIOS DE VERDAD • Objetivos: conocer los criterios de verdad de los conectivos, los cuantificadores y la igualdad. • Saber analizar a partir de ellos, la verdad o falsedad de cualquier enunciado interpretado. Especialmente el caso del condicional.

Negación • "no P" denotada ( P), es verdadera respecto a la interpretación dada, si P es falsa respecto a esa interpretación.

Disyunción • "P o Q" denotada (P Q), es verdadera respecto a la interpretación dada, si P es verdadera respecto a esa interpretación o Q es verdadera respecto a esa interpretación. • Queda incluida aquí la posibilidad de que ambas, P y Q, sean verdaderas respecto a esa interpretación.

Conjunción • "P y Q" denotada (P Q), es verdadera respecto a la interpretación dada, si P es verdadera respecto a esa interpretación, y Q es verdadera respecto a esa interpretación.

Condicional A)“Si P entonces Q” denotada (P Q) es falsa respecto a la interpretación dada, si P es verdadera y Q es falsa, respecto a esa interpretación. B) “Si P entonces Q” denotada (P Q) es verdadera respecto a la interpretación dada, si no es falsa respecto a esa interpretación. Es decir si no sucede que P es verdadera y Q es falsa.

Bicondicional • "P si y sólo si Q" denotada (P Q), es verdadera respecto a la interpretación dada, si ambas P y Q son verdaderas, o bien ambas P y Q son falsas, respecto a tal interpretación.
![Cuantificación Existencial x Qx es verdadera respecto a la interpretación dada si Cuantificación Existencial • [ x Q(x)] es verdadera respecto a la interpretación dada, si](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-32.jpg)
Cuantificación Existencial • [ x Q(x)] es verdadera respecto a la interpretación dada, si hay al menos un individuo en el universo de esa interpretación, tal que Q es verdadera respecto a ese individuo y respecto a esa interpretación.
![Cuantificación Universal x Qx es verdadera respecto a la interpretación dada si Cuantificación Universal • [ x Q(x)] es verdadera respecto a la interpretación dada, si](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-33.jpg)
Cuantificación Universal • [ x Q(x)] es verdadera respecto a la interpretación dada, si para todos los individuos en el universo de esa interpretación, Q es verdadera respecto a cada uno de ellos ahí respecto a esa interpretación.

Verdades Lógicas de LP: TODA FÓRMULA QUE RESULTA VERDADERA, BAJO CUALQUIER INTERPRETACION PARA LOS PREDICADOS Y LAS CONSTANTES DE LA FÓRMULA, Y CUALQUIER ASIGNACIÓN DE INDIVIDUOS A LAS VARIABLES

Ejemplo de Tautología en Lenguaje LP x A V V F V

Ejemplos donde la validez lógica de primer orden coincide con la proposicional • P(c) forma A A “c cumple la propiedad P o no la cumple” [P(c) Q(c)] [ Q(c) P(c)] forma [A B] [ B A] [P(c) Q(c)] forma [A B] [A B]

Ejemplos donde la validez lógica de LP NO coincide con la proposicional o LE [ x y P(x, y)] [ y x P(x, y)] (A B) “Si hay alguien en la relación P con todos entonces para todos hay alguien en la relación P con ellos” P(c) x P(x) (A B) “Si c cumple la propiedad P entonces hay alguien que cumple la propiedad P”
![Un último ejemplo x y Rx y Ry y No Un último ejemplo • x y [ R(x, y) R(y, y) ] • “No](https://slidetodoc.com/presentation_image_h/ac8eabff8d37588d46f90dce9f22fee7/image-38.jpg)
Un último ejemplo • x y [ R(x, y) R(y, y) ] • “No hay en el universo de interpretación un individuo tal que esté en la relación R con todos los individuos (de ahí) que no están en la relación R consigo mismos, y sólo con esos”

¿Sabemos negar? 1. La negación lógica del enunciado “Si te portas bien entonces te llevo al cine” es: a)Si no te portas bien entonces no te llevo al cine b)Si te portas bien entonces no te llevo al cine c) Te portas bien y no te llevo al cine 2. Sean A, B conjuntos y sea w un objeto tal que w A B, entonces: a) w A y w B b) w A o w B 3. La negación lógica de “ser blanco” es: a) ser negro b) no ser blanco c) ser de color distinto al blanco

¿Sabemos negar? 4. La negación lógica de “ 3 < x” es: a) 3 > x b) 3 x c) 3 ≮ x 5. La negación lógica de “Todos los perros ladran” es: a) Hay perros que no ladran b) Ningún perro ladra c) Todos los perros no ladran

Respuestas Correctas: c, b, b, c, a. • 1. La negación lógica del enunciado “Si te portas bien entonces te llevo al cine” es: c) Te portas bien y no te llevo al cine. • 2. Sean A, B conjuntos y sea w un objeto tal que w A B, entonces: b) w A o w B • 3. La negación lógica de “ser blanco” es: b)no ser blanco. • 4. La negación lógica de “ 3 < x” es: c) 3 ≮ x • 5. La negación lógica de “Todos los perros ladran” es: a)Hay perros que no ladran.

Leyes de la Negación • Si P y Q son proposiciones cualesquiera las siguientes son ejemplos de equivalencias lógicas: • P • (P Q) ( P Q) • (P Q) • (P Q) (Q P) • x P • x P x P

Otras Equivalencias Lógicas • • (P Q) ( Q P) (P Q) (P Q) x P x (P Q) ( x P x Q) x (P Q) ( x P x Q)

CONTRAEJEMPLOS • x (P Q) x P x Q Cuando no hay equivalencia la prueba es un contraejemplo

Símbolo para Consecuencia Lógica _______

Símbolo para Consecuencia Lógica Premisas _______ Conclusión

Ejemplo de Razonamiento en LP P(a) Q(c) _________________ P(a)

Prueba de validez lógica por tablas de verdad. PREMISAS CONCLUSION P(a) Q(c) P(a) V V V F F V F F V F F V V F V F F V V P 1 P 2 C

Ejemplo de Razonamiento en LP x [ B(x) y [ R(x, y) R(y, y) ]] __________________________________________________ x B(x)

Prueba de validez lógica de razonamientos en lenguaje coloquial: • Traducir del lenguaje coloquial a LP • Determinar la validez proposicional de la traducción por tablas de verdad • Si es valido proposicionalmente, entonces es valido en LP • Si no, entonces aplicar criterios de verdad de igualdad y cuantificadores (no hay algoritmo)

Diferencias entre lógica proposicional y lógica cuantificacional • ¿No importa qué son A, B, C realmente? ¡En primer orden si importa! A x P(x) B C P(a) Q(a) C Q(a) ________________ _______________________ NO ES INF. CORRECTA SI ES INF. CORRECTA PROPOSICIONAL EN PRIMER ORDEN • A P(c) B c = b C P(b) • NO ES INF. CORRECTA SÍ ES INF CORRECTA!

Un razonamiento en lenguaje coloquial Todos los borogroves son kismis, si alguien tirila. Nito tirila y Pac es un borogrove. _________________________________________________________________ Por lo tanto, Pac es un kismi.

Traducción del Razonamiento • B: predicado ser borogrobe • • K: predicado ser kismi T: predicado tirila (del verbo “tirilar”) n: constante para el individuo Nito p: constante para el individuo Pac • ( x. T(x)) x[B(x) K(x)] • T(n) B(p) • K(p)

Un razonamiento en lenguaje coloquial Todos los borogroves son kismis, si alguien tirila • x. T(x) x[B(x) K(x)] Nito tirila y Pac es un borogrove T(n) B(p). T(n) x. T(x) x[B(x) K(x)] [B(p) K(p)] K(p). Por lo tanto, Pac es un kismi.

¿QUE ES UN ARGUMENTO? • Un argumento es un conjunto finito ordenado de afirmaciones de las cuales se dice que la última (conclusión), se sigue de las anteriores (premisas). Un argumento es: lógicamente correcto o lógicamente incorrecto

¿QUÉ ES UN ARGUMENTO CORRECTO? Un argumento es lógicamente correcto si y sólo si sucede que: sin importar la interpretación, Si todas las premisas son verdaderas, la conclusión debe ser necesariamente verdadera. Dicho de otra manera, es lógicamente correcto, si no hay interpretación alguna para la cual las premisas sean todas verdaderas y la conclusión sea falsa.

• Hay ejemplos de los cuatro tipos de argumentos: Correcto conclusión verdadera Correcto conclusión falsa Incorrecto conclusión verdadera Incorrecto conclusión falsa • (Aquí verdadera o falsa es respecto a la interpretación natural)

Esto es correcto conclusión falsa? O incorrecto conclusión verdadera?

ALGUNAS PRECISIONES • Obsérvese que en un argumento correcto, si las premisas son todas verdaderas, la conclusión será necesariamente verdadera. • Por lo tanto, en un argumento correcto, si la conclusión es falsa, entonces al menos una de las premisas debe ser falsa. • ¡No importa la interpretación!

MEDITACIÓN • Si un argumento es incorrecto, lo único que podemos decir es que hay una interpretación para la cual las premisas son verdaderas y la conclusión es falsa. • Pero con otras interpretaciones puede suceder cualquiera otra cosa.

EJEMPLOS Considere el siguiente argumento: • Juan vendrá, si hay buen día. No hay buen día. • Juan no vendrá • a) El argumento es lógicamente correcto? b) El argumento es lógicamente incorrecto?

EJEMPLOS • Juan vendrá, si hay buen día. No hay buen día. • Juan no vendrá • El argumento es lógicamente incorrecto: la conclusión no se sigue de las premisas. Es posible una interpretación donde las premisas sean verdaderas y la conclusión falsa.

Una última observación Si en un argumento, la conclusión es falsa con alguna interpretación, sólo podemos concluir que: o bien el argumento es incorrecto, o bien alguna de las premisas es falsa.

Ahora bien: • ¿Cómo podemostrar que un argumento incorrecto es efectivamente incorrecto? • La manera de hacerlo es dando una interpretación conveniente al lenguaje involucrado, de modo que resulte que las premisas sean todas verdaderas y la conclusión sea falsa.

Ejemplos con interpretación natural: A)ARGUMENTO CORRECTO C)ARGUMENTO INCORRECTO CON CONCLUSIÓN VERD. Todo hombre es mortal. Todo pingüino es ave. Sócrates es hombre. Mi perro no es pingüino. Sócrates es mortal Mi perro no es ave. B)ARGUMENTO CORRECTO D) ARGUMETO INCORRECTO CONCLUSIÓN FALSA CONCLUSIÓN FALSA Toda ave es voladora. Todo pez es nadador. El avestruz es ave. El delfín no es pez(mamíf) El avestruz es volador El delfín noes nadador

Los dos ejemplos de argumentos incorrectos C) y D) tienen la misma forma • El hecho de que la conclusión pueda ser verdadera (con la interpretación usual) es una contingencia. • Es decir, se debe a la casualidad, si únicamente consideramos las premisas dadas.

Para demostrar que el argumento C) es incorrecto, la interpretación natural no sirve. Pero basta con cambiar “ave” por “animal” Otra interpretación con igual forma lógica respecto a la cual las premisas son verdaderas y la conclusión falsa: • Todo pingüino es animal. • Mi perro no es pingüino. • Mi perro no es animal.

Ejemplos de argumentos, con la interpretación natural de la aritmética, son los siguientes: A)ARGUMENTO CORRECTO C)ARGUMENTO INCORRECTO CONCLUSIÓN VERD Todo múltiplo de 6 Todo número con exactamente es múltiplo de 3. dos divisores es primo. 12 es múltiplo de 6. 4 no tiene exactamente dos divisores(Tiene tres: 1, 2, 4) 12 es múltiplo de 3. 4 no es primo. n B)ARGUMENTO CORRECTO D)ARGUMETO INCORRECTO CON CONCLUSIÓN FALSA Todo múltiplo de 4 es par. Todo múltiplo de 6 es par. 5 es múltiplo de 4. 8 no es múltiplo de 6. 5 es par. 8 no es par.

Para demostrar que el argumento C) es incorrecto, la interpretación natural no sirve, pues tanto las premisas como la conclusión son verdaderas. Damos otra interpretación con igual forma lógica respecto a la cual las premisas son verdaderas y la conclusión falsa: • Todo polinomio con exactamente dos raíces es cuadrático. • X 2 4 x+4 no tiene exactamente dos raíces. (Su única raíz (doble) es 2) • X 2 4 x + 4 no es cuadrático.

¿Y cómo demostramos la correctud de un argumento? • La manera directa de demostrar que un argumento es correcto, consiste en suponer verdaderas todas las premisas pero sin tomar en cuenta ninguna interpretación particular. A partir de eso, usando únicamente los criterios de verdad, hacer ver que la conclusión es necesariamente verdadera.

La manera indirecta • En algunos casos la manera directa no es posible, por lo que hay que hacerlo de modo indirecto: por reducción al absurdo, es decir suponiendo que hubiera una interpretación respecto a la cual todas las premisas fueran verdaderas y la conclusión fuera falsa. A partir de ahí, llegar a una contradicción.

Escribir el número y su respuesta 1. Considere el siguiente argumento: • Todos los borogroves son kismis, si alguien tirila. • Nito tirila y Pac es un borogrove. • Pac es un kismi. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

Escribir el número y su respuesta 2. Considere argumento: el siguiente • Todos le tienen miedo a Drácula. • Drácula sólo le tiene miedo a William. • William es Drácula. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

Escribir el número y su respuesta 3. Considere el siguiente argumento: • Si hoy es jueves entonces mañana será viernes. • Mañana será viernes. • hoy es jueves. a) El argumento es lógicamente correcto b)El argumento es lógicamente incorrecto

4. Considere el siguiente argumento: • Juan es hermano de todos los hermanos de Roberto. • Juan no es hermano de sí mismo Juan no es hermano de Roberto a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

5. Considere el siguiente argumento: • X es un número menor que todos los números menores que Y. • X no es menor que X. • X no es menor que Y. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

6. Considere el siguiente argumento: • Algunos humanos son mexicanos. • Algunos mexicanos fuman. • Algunos humanos fuman. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

7. Considere el siguiente argumento: • Hay una lanza que perfora a todos los escudos. • Hay un escudo al que no lo perfora ninguna lanza. • Hay una lanza que perfora y no perfora a un escudo. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

8. Considere el siguiente argumento: • • 2 divide al numerador de 6/8 = 3/4. • 2 divide al numerador de 3/4 a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

9. Considere el siguiente argumento: • Romeo ama a Julieta. • Julieta es una palabra de siete letras. • Romeo ama a una palabra de siete letras. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

10. Considere el siguiente argumento: • Cualquier barbero de Ensenada, rasura a todos los hombres de Ensenada que no se rasuran a sí mismos y sólo a esos. • No hay barberos en Ensenada. a) El argumento es lógicamente correcto b) El argumento es lógicamente incorrecto

Respuestas Correctas: 1. a) 2. a) 3. b) 4. a) 5. a) 6. b) 7. a) 8. a) 9. a) 10. a)

ENFOQUE AXIOMÁTICO • Sistematización de razonamientos válidos y fórmulas lógicamente válidas de LP • Mediante un sistema formal axiomático: axiomas y reglas de inferencia • Mediante un sistema formal de deducción natural: sólo reglas

En el caso de LP, se han construido sistemas formales completos: • Permiten derivar todas las fórmulas universalmente válidas • Permiten derivar todos los razonamientos válidos en LP

Y por otro lado, son correctos • Toda fórmula derivable en tales sistemas formales es una verdad lógica • Todo razonamiento derivable de tales sistemas es válido

REGLAS DE INFERENCIA CUANTIFICACIONALES • La letra φ denota fórmulas, las letras x, y, z denotan variables. • La letra t denota términos: variables, constantes o funciones aplicadas a términos. • Es muy importante precisar con rigor las restricciones. Es común cometer errores o entender mal estas reglas.

1. IU INSTANCIACIÓN UNIVERSAL • xφ(x) ___________________________________ φ(t) resulta de sustituir t en los lugares de las presencias libres de x en φ(x) Ejemplos: x P(x) P(c) • x. R(a, x) x y. R(x, y) R(a, b) y. R(c, y) y. R(z, y) ___________________________________ _________________________________________ _________________________________________________

1. IU INSTANCIACIÓN UNIVERSAL Restricción: Si t es una variable y, o bien y aparece en t, entonces ninguna presencia de x en φ(x) debe estar afectada por un cuantificador con esa variable y. Ejemplos de Error: • x y. R(x, y) x y [P(x) P(y)] _________________________________________________ _____________________________________________________________________ y. R(y, y) y [P(y)]

2. GE GENERALIZACIÓN EXISTENCIAL • φ(t) __________________ x φ(x) φ(t) resulta de sustituir t en los lugares de las presencias libres de x en φ(x) Ejemplos: P(c) ________________ x P(x) • R(a, b) R(a, b) P(a) x R(x, b) x [R(x, b) P(x)] _________________ ________________________________

2. GE GENERALIZACIÓN EXISTENCIAL Misma restricción de IU: Si t es y, o bien y aparece en t, entonces ninguna presencia de x en φ(x) debe estar afectada por un cuantificador con esa variable y. Ejemplos de Error: • y R(y, y) y [P(y) Q(y)] _________________________________________________ ___________________________________________________________________ x y R(x, y) x y [P(y) Q(x)]

3. GU GENERALIZACIÓN UNIVERSAL • Si x es variable que no aparece libre en fórmulas de Γ y además Γ├ φ(x), entonces Γ├ x φ(x) Intuición: Si podemos probar φ(x) sin ninguna suposición sobre x, podemos por ser arbitrario, afirmar que x φ(x) Obs: P(x)├ P(x), pero P(x) ⊬ x P(x) • Ejemplo: x y φ(x, y)├ y x φ(x, y)

3. GU GENERALIZACIÓN UNIVERSAL 1. x y φ(x, y)├ y φ(x, y) IU(t=x) 2. y φ(x, y)├ φ(x, y) IU(t=y) 3. x y φ(x, y)├ φ(x, y) Trans 1, 2 4. x y φ(x, y)├ x φ(x, y) GU, 3

4. IE INSTANCIACIÓN EXISTENCIAL • Si c es una constante nueva que no aparece en φ(x), ni en ψ, ni en Γ, y además Γ, φ(c)├ ψ entonces Γ, xφ(x) ├ ψ • IE no afirma que xφ(x)├ φ(c) Esto es falso, por ejemplo: x Vuela (x) ⊬ Vuela (juan)

4. IE INSTANCIACIÓN EXISTENCIAL • Si c es una constante que no aparece en φ(x), ni en ψ, ni en Γ, y además Γ, φ(c)├ ψ entonces Γ, xφ(x) ├ ψ • Intuición: Supongamos que sabemos que hay x tal que cumple φ. Es decir sabemos que xφ(x). Llamemos “c” a tal individuo. Ahora, si a partir de φ(c) probamos ψ, entonces podemos probar ψ

4. IE INSTANCIACIÓN EXISTENCIAL Ejemplo: x y P(x, y) ├ y x P(x, y) Por la regla IE, es suficiente probar: y P(c, y) ├ y x P(x, y). Donde c es una constante nueva que no aparece en φ(x) = y P(x, y) ni en ψ = y x P(x, y), ni en Γ = ø

4. IE INSTANCIACIÓN EXISTENCIAL Prueba de: y P(c, y)├ y x P(x, y) 1. y P(c, y)├ P(c, y) IU(t=y) 2. P(c, y)├ x P(x, y) GE(t=c) 3. y P(c, y)├ x. P(x, y) Trans 1, 2 4. y P(c, y)├ y x. P(x, y) GU, 3 (y NO LIBRE EN HIPOTESIS) x y. P(x, y)├ y x. P(x, y) IE, 4

RAZONAMIENTO AUTOMÁTICO Procedimientos de prueba automática de teoremas en cualquier teoría finitamente axiomatizable en un lenguaje de primer orden con igualdad. Para cualquier conjunto finito de enunciados A 1, . . . , An y cualquier enunciado B en un lenguaje de primer orden con igualdad. ¿ A 1, . . . , An B ?

Teorema Para cualquier conjunto finito de enunciados A 1, . . . , An y cualquier enunciado B en un lenguaje de primer orden con igualdad: B es teorema a partir de A 1, . . . , An sí y sólo sí el procedimiento así lo indica

Ejemplos Prueba de la cancelación para la multiplicación a partir de los axiomas de grupo. 2. Prueba de que una relación R es reflexiva, suponiendo que R sea simétrica, transitiva y “sin puntos aislados” (para todo x hay un z tal que x está R-relacionado con z o z está R-relacionado con x) 1.

Dos ejemplos sencillos (argumentos) • La conclusión del argumento es un “teorema” a partir de las premisas, que serán las hipótesis. ARGUMENTO 1: Juan es hermano de todos los hermanos de Roberto. Juan no es hermano de sí mismo. Juan no es hermano de Roberto. • ARGUMENTO 2: Todos le tienen miedo a Drácula sólo le tiene miedo a Pedro es Drácula.

PRERREQUISITOS 1. HACEMOS LA TRADUCCIÓN Y LO VEMOS COMO CONSECUENCIA LÓGICA • A 1, . . . , An B 2. TEOREMA BÁSICO PARA PRUEBAS POR REFUTACIÓN: A 1, . . . , An B si y sólo si (A 1 . . . An B) no es satisfacible 3. TRANSFORMACIÓN A FORMA CLAUSULAR (CONJUNCIÓN DE CLÁUSULAS) Las cláusulas son disyunciones de atómicas o atómicas negadas. Toda fórmula A puede transformarse a una conjunción de cláusulas, llamada forma clausular denotada CL (A). (A 1 . . . An B) ~ ~ ~> CL(A 1 . . . An B)

Teorema de Skolem: • A es insatisfacible si y sólo si CL(A) es insatisfacible • MÁS GENERALMENTE: • Un conjunto de enunciados es insatisfacible si y sólo si el conjunto de formas clausulares de ellos es insatisfacible.

REGLA DE RESOLUCIÓN (Robinson 1965) • La regla RESOLUCIÓN generaliza al silogismo disyuntivo: • • A B ¬A _____________ • B • A CASOS COMO: • • A B ¬D ¬A C ¬E ___________________________ B C ¬D ¬E

La regla Resolución nos permite hacer todas las inferencias de tipo: • • L Q 1 . . . Qm ¬L R 1 . . . Rn ________________________________ • Q 1 . . . Qm R 1 . . . Rn Cláusulas Padres __________ Resolvente • ¿Y en el caso especial de tener como cláusulas padres a L y ¬L? El resolvente es nada y lo llamamos cláusula vacía denotado ڤ y significa que hubo una contradicción o es insatisfacible

RESOLUCIÓN CON UNIFICACIÓN Q(x, b) P(x, a) • ¬ Q(a, w) R(w, b) • ------------------ P(a, a) R(b, b) • u {x/a, w/b} es el unificador • Obsérvese que al hacer la sustitución del unificador Q(x, b) y ¬Q(a, w) quedan como: Q(a, b) y ¬Q(a, b) por lo que se eliminan. Desde luego el resolvente queda afectado por la sustitución.

Teorema de Loveland • Si K es un conjunto de cláusulas de un lenguaje de primer orden con igualdad, entonces: K es insatisfacible si y sólo si hay una deducción de la cláusula vacía ڤ a partir de K, usando únicamente resolución.

COROLARIO: D. A. T. Si B es teorema a partir de A 1, . . . , An: 1. Negar B ( B) 2. Formar el conjunto K = {¬B, A 1, . . . , An} en forma clausular. 3. Aplicar pasos de resolución a K hasta obtener la cláusula vacía ڤ. B es teorema a partir de A 1, . . . , An si y sólo si se obtiene la cláusula vacía ڤ , a partir de K.

EJEMPLO 1 Juan es hermano de todos los hermanos de Roberto. Juan no es hermano de sí mismo. Juan no es hermano de Roberto • SIMBOLIZACIÓN DE CONSECUENCIA LÓGICA: • x [H(x, r) H(j, x)], H(j, j) H(j, r) • Por Teo. Básico, No Satisfacible: • x[H(x, r) H(j, x)], H(j, j), H(j, r) • Por Teo Skolem, No Satisfacible: • K= { [ H(x, r) H(j, x)], H(j, j), H(j, r) } • • X/j ڤ RESOLUCIÓN TEO. LOVELAND

EJEMPLO 2 Todos le tienen miedo a Drácula sólo le tiene miedo a Pedro es Drácula. • SIMBOLIZACIÓN DE CONSECUENCIA LÓGICA: • x[M(x, d)], x[M(d, x) (x=p)] (p=d) • Por Teo. Básico, No Satisfacible: • x[M(x, d)] , x[M(d, x) (x=p)] , (p d) • Por Teo. Skolem, No Satisfacible: • K = { M(x, d), [ M(d, x) (x = p)], (p d) } • • X/d ڤ Resolución y Paramodulación TEO. LOVELAND

PROGRAMA LÓGICO P padre(x, y) padre(y, z) abuelo(x, z) • • • hijo(x, y) padre(y, x) padre(juan, raul). hijo(juan, roberto). Pregunta: ? abuelo(roberto, w) Respuesta: w = raul Significado: P abuelo(roberto, raul)


BIBLIOGRAFIA BASICA • La enseñanza del análisis lógico, J. A. Amor, en La Razón Comunicada II, TDL, 2003. • Introducción a la lógica, LTF Gamut, Editorial Eudeba, Argentina, 2002. • Lógica clásica de primer orden con igualdad, J. A. Amor, notas de clase.

BIBLIOGRAFÍACOMPLEMENTARIA • Amor J. A. , Paradojas, intuición y lógica, revista Ciencias no. 29, Facultad de Ciencias, UNAM, 1993. • Easley, J. A. Lógica y heurística en la reforma curricular de las matemáticas, Matemáticas y Enseñanza, Nos. 7 y 8, SMM, 1976. • Solow, D. Cómo entender y hacer demostraciones en matemáticas, Limusa, 1987. • Polya, G. , Cómo plantear y resolver problemas, Editorial Trillas, 1965. • Smullyan Raymond, ¿Cómo se llama este libro? , Editorial Cátedra colec. Teorema, 1978. • Tarski Alfred, Truth and proof, Scientific American, junio 1969. • Torres Torija, Planteo y resolución de problemas, Editorial Trillas, 1976.

MÁS BIBLIOGRAFÍA COMPLEMENTARIA • Barwise, Jon et. al. Handbook of mathematical logic Amsterdam: North Holland, 1977. • Una introducción Matemática a la lógica, 2 a. Edicion, E. Enderton, traducción de J. A. Amor, IIF UNAM, 2004. Version original: A mathematical introduction to logic, 2 nd. edition, E. Enderton, Academic Press, 2001. • Mendelson, Elliot. Introduction to mathematical logic. Pacific Grove, California: Wads worth, 1987. • Suppes, Patrick Colonel. Introducción a la lógica simbólica. Tr. por Gabriel Aguirre Carrasco. México: Continental, 1956
 Si logica
Si logica Amor 1 amor 2 amor 3
Amor 1 amor 2 amor 3 Plc semimodular
Plc semimodular Logica de orden superior
Logica de orden superior Periodo de los numeros
Periodo de los numeros Aplicaciones de ecuaciones diferenciales de primer orden
Aplicaciones de ecuaciones diferenciales de primer orden Respuesta de
Respuesta de Linealidad ecuaciones diferenciales
Linealidad ecuaciones diferenciales Sistemas de primer orden
Sistemas de primer orden Conceptos de primer orden ejemplos
Conceptos de primer orden ejemplos Tarea 1- ecuaciones diferenciales de primer orden
Tarea 1- ecuaciones diferenciales de primer orden _
_ Sistemas de segundo orden
Sistemas de segundo orden Ecuaciones diferenciales ordinarias de primer orden
Ecuaciones diferenciales ordinarias de primer orden Estructuras de textos literarios
Estructuras de textos literarios Caracteristicas de un escultor
Caracteristicas de un escultor Funciones del complemento
Funciones del complemento Ramas del derecho publico
Ramas del derecho publico Arquitectura de von neumann mapa conceptual
Arquitectura de von neumann mapa conceptual Elementos de probabilidad
Elementos de probabilidad Características de la teoría científica
Características de la teoría científica Perspectiva clasica
Perspectiva clasica Literatura clasica oriental
Literatura clasica oriental Tipos de balanza
Tipos de balanza Literatura clasica antecedentes
Literatura clasica antecedentes Conclusión de la geopolítica
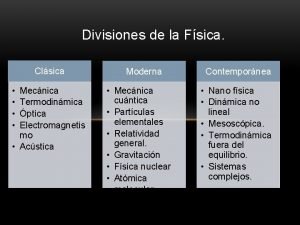
Conclusión de la geopolítica Division de la fisica moderna
Division de la fisica moderna Ramas de la física moderna
Ramas de la física moderna Fisica clasica linea del tiempo
Fisica clasica linea del tiempo Mecanica clasica
Mecanica clasica Logistica clasica
Logistica clasica Democracia clásica u occidental definicion
Democracia clásica u occidental definicion Harrington emerson administracion cientifica
Harrington emerson administracion cientifica Empec
Empec Tengo contra ti que has perdido tu primer amor
Tengo contra ti que has perdido tu primer amor Has dejado tu primer amor
Has dejado tu primer amor El amor es comprensivo el amor es servicial
El amor es comprensivo el amor es servicial Amor amor ruben morre
Amor amor ruben morre De manhã bem cedo busco de jesus a direção
De manhã bem cedo busco de jesus a direção Frases de terminar una relación
Frases de terminar una relación El amor es compasivo el amor es servicial san pablo
El amor es compasivo el amor es servicial san pablo Colegio alfredo binet
Colegio alfredo binet Alfredo arraut
Alfredo arraut Padre alfredo feretti
Padre alfredo feretti Alfredo molina triana
Alfredo molina triana Alfredo marques gubern
Alfredo marques gubern Alfredo embid
Alfredo embid Alfredo cuervo barrero
Alfredo cuervo barrero Alfredo balena
Alfredo balena Membrane osmometry molecular weight
Membrane osmometry molecular weight Alfredo cuervo barrero
Alfredo cuervo barrero 4 reformas de alfredo gonzales flores
4 reformas de alfredo gonzales flores Alfredo cuervo barrero
Alfredo cuervo barrero Anisomiopia
Anisomiopia Alfredo morel
Alfredo morel Alfredo ferrero costa
Alfredo ferrero costa Alfredo alberti
Alfredo alberti Stefano di carlo polito
Stefano di carlo polito Comic prohibido
Comic prohibido Alfredo rial
Alfredo rial Chef alfredo villalba
Chef alfredo villalba Alfredo cuervo barrero
Alfredo cuervo barrero Caracter juridico
Caracter juridico Alfredo rendon impi
Alfredo rendon impi Alfredo embid
Alfredo embid Alfredo martinez perez
Alfredo martinez perez Alfredo ramos martinez
Alfredo ramos martinez Pepe and alfredo are resting on an offshore raft
Pepe and alfredo are resting on an offshore raft Alfredo cuervo barrero
Alfredo cuervo barrero Alfredo dupasquier incidente
Alfredo dupasquier incidente Coma lattacidemico
Coma lattacidemico Alfredo embid
Alfredo embid Alfredo carpineti
Alfredo carpineti Usenet message alfredo
Usenet message alfredo Ies alfredo brañas
Ies alfredo brañas Alfredo cuervo barrero
Alfredo cuervo barrero Otg
Otg Alfredo embid wikipedia
Alfredo embid wikipedia Alfredo embid
Alfredo embid Habitao
Habitao Alfredo cuervo barrero
Alfredo cuervo barrero Alfredo egydio setubal
Alfredo egydio setubal Alfredo di tillio
Alfredo di tillio The sound of silence alfredo jaar
The sound of silence alfredo jaar Alfredo marcos
Alfredo marcos Alfredo capote
Alfredo capote Antonio alfredo ferreira loureiro
Antonio alfredo ferreira loureiro Alfredo marques gubern
Alfredo marques gubern Alfredo molina triana
Alfredo molina triana Alfredo cuervo barrero
Alfredo cuervo barrero Teniente coronel alfredo bonifaz
Teniente coronel alfredo bonifaz Alfredo cuervo barrero
Alfredo cuervo barrero Alfredo cuervo barrero
Alfredo cuervo barrero Actriz reeditada como bella ceci
Actriz reeditada como bella ceci Queda prohibido llorar sin aprender
Queda prohibido llorar sin aprender Tarjetas de triage
Tarjetas de triage Alfredo cristiano
Alfredo cristiano Alfredo anania
Alfredo anania Alfredo rendon impi
Alfredo rendon impi Alfredo chaparro muñoz
Alfredo chaparro muñoz Urechi jos implantate
Urechi jos implantate Jos t
Jos t Hrv narodni preporod
Hrv narodni preporod Jos jaspars
Jos jaspars Rotunjiti la sute de mii numarul natural n
Rotunjiti la sute de mii numarul natural n Jos app
Jos app Urechi jos implantate
Urechi jos implantate Citiți cu atenție textul de mai jos
Citiți cu atenție textul de mai jos Université dunărea de jos
Université dunărea de jos Arie triunghi isoscel
Arie triunghi isoscel Luca stalin
Luca stalin Još hrvatska ni propala tekst
Još hrvatska ni propala tekst Maria jos
Maria jos Wayfaring stranger 1917 scene
Wayfaring stranger 1917 scene Bahs jos
Bahs jos