Logic Review FORMAT Format Part I 30 questions

Logic Review

FORMAT

Format Part I • 30 questions • 2. 5 marks each • Total 30 x 2. 5 = 75 marks Part II • 10 questions • Answer only 5 of them! • Total 5 x 5 marks each = 25 marks

Part I The questions in Part I are multiple choice. About 8 -10 out of the questions in Part I (30 total) are about argument analysis and logic. ~20 -25% of the total marks.

Part II contains mostly logic questions, about 9 out of 10. You are only required to answer 5 of the 10 questions. If you answer more than 5, I will only mark the first 5. Part II is much harder than Part I.

LOGICAL CONCEPTS

Logical Concepts on the Final About 6/30 multiple choice questions deal with argument analysis (identification of premises and conclusions) and logical concepts (validity, soundness, logical equivalence, etc. ). Therefore mastering these concepts can go a long way toward the grade you get on the Final, up to about 15%.

What to Study • Read Joe Lau’s modules on Argument Analysis and Meaning Analysis (recommended reading, Week 14). • Read the powerpoint slides from 25/4 • Read the logic slides in Week 5.

Arguments (in philosophy) are a collection of premises (possibly zero) given in support of a conclusion.

Argument Analysis You will be asked to identify premises and conclusions in questions, and to identify hidden assumptions. These questions are not hard if you think about them and know the ideas.

Validity To say that an argument is valid is to say: If all of the premises of the argument are true, then the conclusion must be true.

Validity For the final you should memorize the definition of validity. Furthermore, you should be able to answer some basic questions about the definition.

Examples Can a valid argument have false premises? Can it have a true conclusion? Can it have false premises and a false conclusion? Can it have true premises and a false conclusion?

Inductive Validity You need to know the definition of inductively valid/ inductively strong arguments. First: inductively valid = inductively strong. An argument is inductively strong if when all the premises are true, the conclusion is very likely to be true (has a high probability of being true).

Note If the final asks you about a “valid argument” assume that it means “deductively valid argument. ” We will always say “inductively valid (strong)” when we mean that.

Logical Equivalence Two sentences A and B are logically equivalent when A├ B and B├ A. In other words, A and B are logically equivalent when “A therefore B” and “B therefore A” are both valid arguments. In other words A is true if and only if B is true.

Soundness To say that an argument is sound is to say: The argument is valid AND it has true premises. You need to memorize this definition and be able to answer some basic questions about it. Can a sound argument have a false conclusion? Etc.

SENTENTIAL LOGIC

SL on the Final There aren’t a lot of multiple choice questions about SL (there are only 30 questions total), but there are several short answer questions (Part II) that involve (or can involve) SL. Knowing SL perfectly can count for up to about 20% of the marks on the final.

What to Study • Read Joe Lau’s Sentential Logic Module (on the readings list for Week 5). • Read all the powerpoint slides from Weeks 5 and 6. If you know all that material, you are as well prepared for the logic questions as you can be.

Difficulty Some of the questions are hard, and even made me stop and think about them. They are supposed to be like that. Difficult questions help differentiate students. The exam will be curved and the same number of students will get A’s in this class as in any other class.

Proofs There are two proofs on the optional section. They are not easy, but if you are good at proofs, you might consider answering them. If you don’t like proofs don’t bother studying them. You can always choose 5 questions on Part II that do not involve proofs.

Translations You need to memorize the standard translations for the logical connectives into English, both because you will be asked questions about which English sentence translates some predicate logic sentence and because you will be asked which predicate logic sentence translates some English sentence.

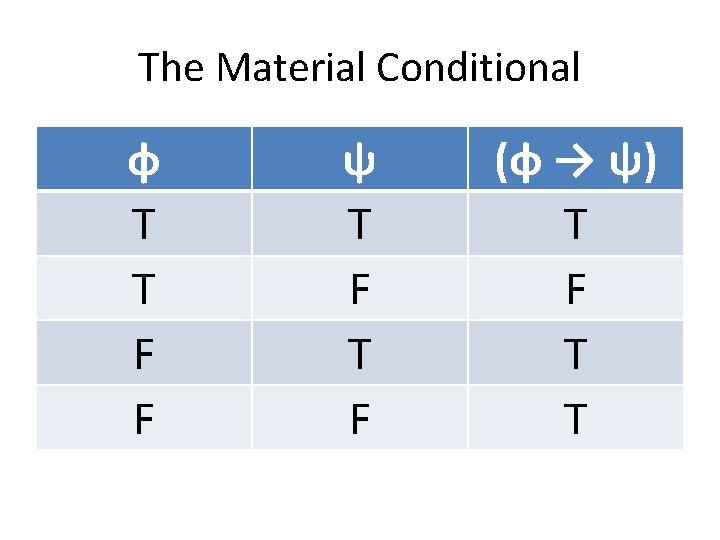
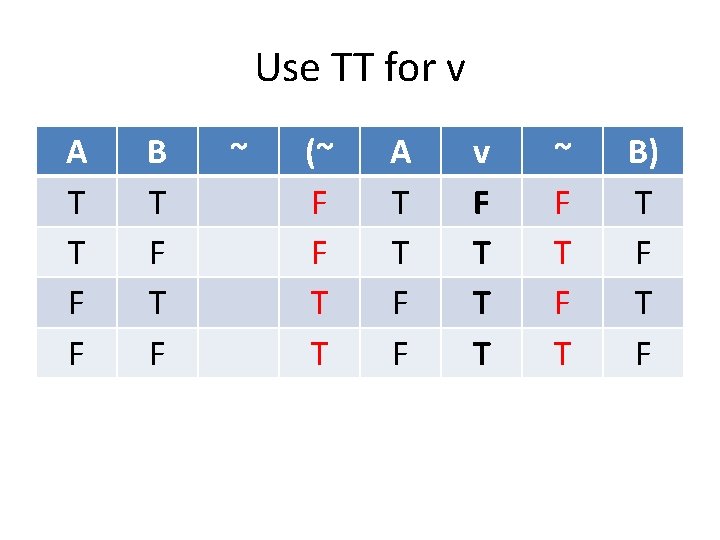
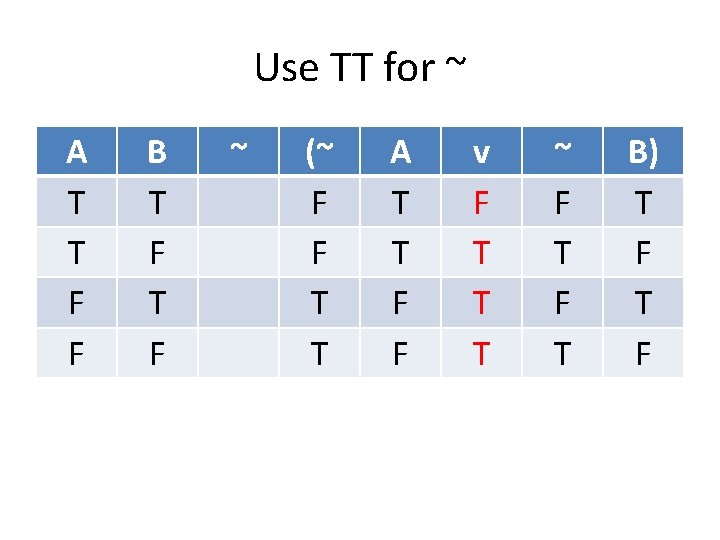
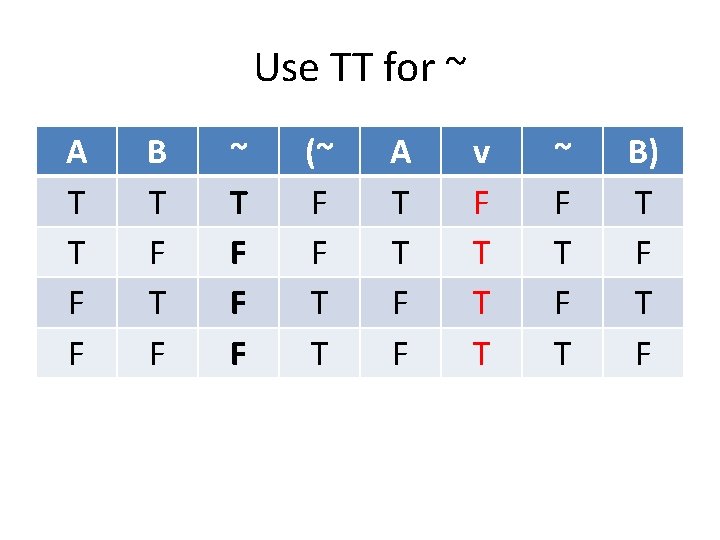
Standard Translations ~A: not A, A is false, A is not true, it’s not the case that A (A & B): A and B, A but B, although A, B (~A & ~B): neither A nor B (A v B): A or B, A unless B (A → B): if A then B, A only if B, B if A (A ↔ B): A if and only if B

“If” and “Only if” The most difficult part of translations is “if” and “only if” and “if and only if” “If A then B” “A only if B” “B if A”: (A → B) “If B then A” “B only if A” “A if B”: (B → A) “A if and only if B” “B if and only if A”: (A ↔ B)

Example Problem (((P v Q) v R) → (S v (T & U)))… a. b. c. d. …is true if S is true …is true if T and U are false …is true if R is false …is false only if S is false

Truth-Table Won’t Work This seems like a hard problem at first sight. A truth-table would take too much time to construct. It would have to have 2 x 2 x 2 x 2 = 64 rows! Let’s consider it intelligently.

True Conditionals When is (((P v Q) v R) → (S v (T & U))) true? It’s a conditional, so it’s true whenever either • ((P v Q) v R) is false • Or (S v (T & U)) is true

The Material Conditional φ T T F F ψ T F (φ → ψ) T F T T

False Conditionals Additionally (((P v Q) v R) → (S v (T & U))) is false when: • ((P v Q) v R) is true • And (S v (T & U)) is false

Example Problem (((P v Q) v R) → (S v (T & U)))… a. b. c. d. …is true if S is true …is true if T and U are false …is true if R is false …is false only if S is false

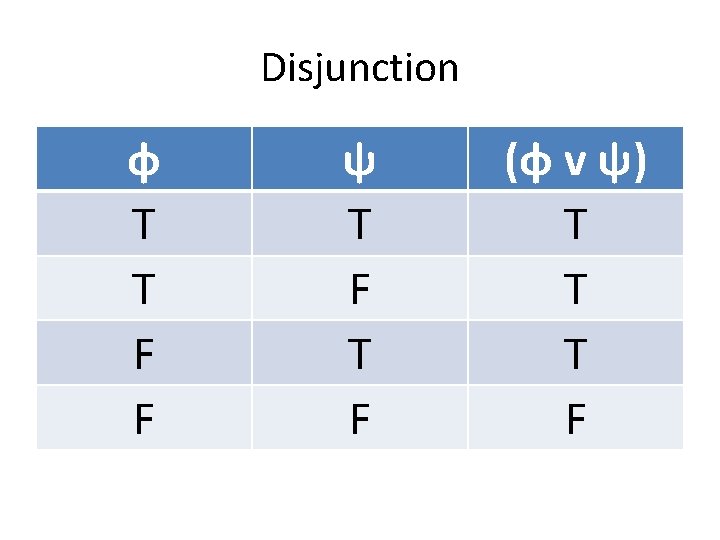
Disjunction If S is true, then (S v (T & U)) is true, because disjunctions are true when either disjunct is true.

Disjunction φ T T F F ψ T F (φ v ψ) T T T F

Not (a) So if S is true, (S v (T & U)) is true. But then (((P v Q) v R) → (S v (T & U))) could be false, if ((P v Q) v R) is false. So (a) is not the right answer.

Example Problem (((P v Q) v R) → (S v (T & U)))… a. b. c. d. …is true if S is true …is true if T and U are false …is true if R is false …is false only if S is false

Not (b) If T and U are false, then (T & U) is false. But this tells us nothing about whether (S v (T & U) is true or false, because if S is false, it is false and if S is true it is true. Therefore we don’t know whether (((P v Q) v R) → (S v (T & U))) is true or false. So (b) is wrong.

Example Problem (((P v Q) v R) → (S v (T & U)))… a. b. c. d. …is true if S is true …is true if T and U are false …is true if R is false …is false only if S is false

Not (c) If R is false, then ((P v Q) v R) can be either true or false. For example, it will be true if P is true or if Q is true, and only false when P and Q are both false. Assuming R is false, ((P v Q) v R) might be true, and therefore the whole sentence could be false (antecedent true, consequent false).

Example Problem (((P v Q) v R) → (S v (T & U)))… a. b. c. d. …is true if S is true …is true if T and U are false …is true if R is false …is false only if S is false

Why (d)? By process of elimination, you know the answer is (d). But why is it the right one? “A only if B” means if A, then B. (((P v Q) v R) → (S v (T & U))) is false only if S is false If (((P v Q) v R) → (S v (T & U))) is false, then S is false.

Why (d)? If (((P v Q) v R) → (S v (T & U))) is false Then ((P v Q) v R) is true And (S v (T & U)) is false. If (S v (T & U)) is false then (T & U) is false And S is false.

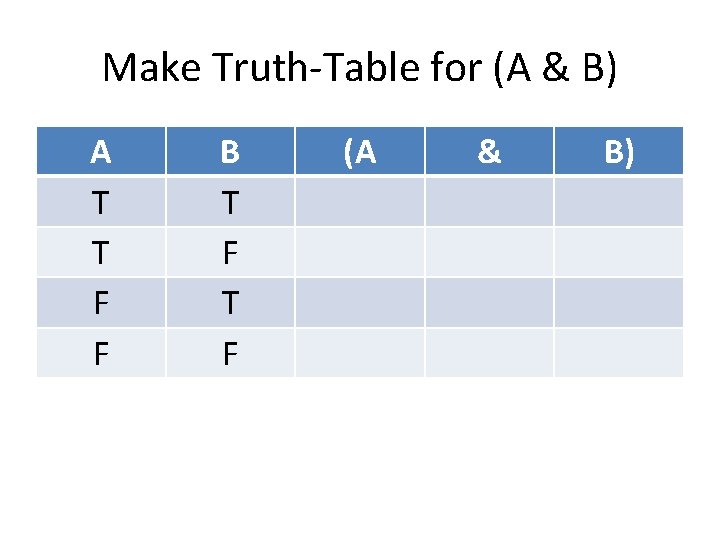
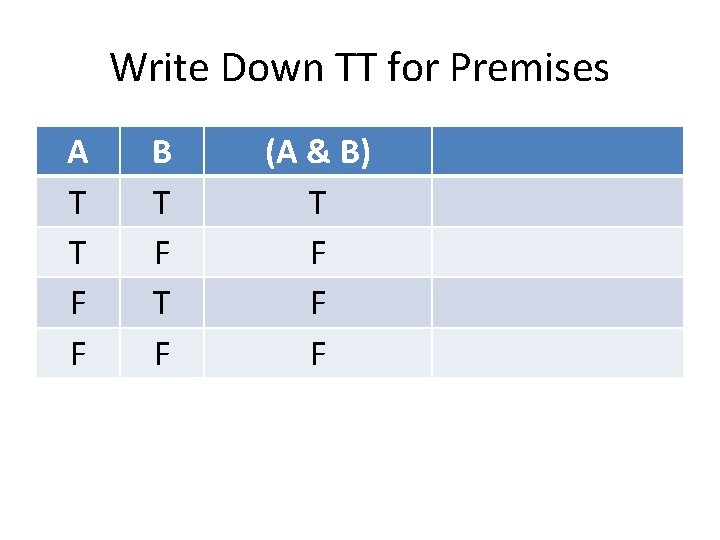
Example Problem 2 Use a truth-table to determine whether a logically entails b. a. (A & B) b. ~(~A v ~B)

Make Truth-Table for (A & B) A T T F F B T F (A & B)

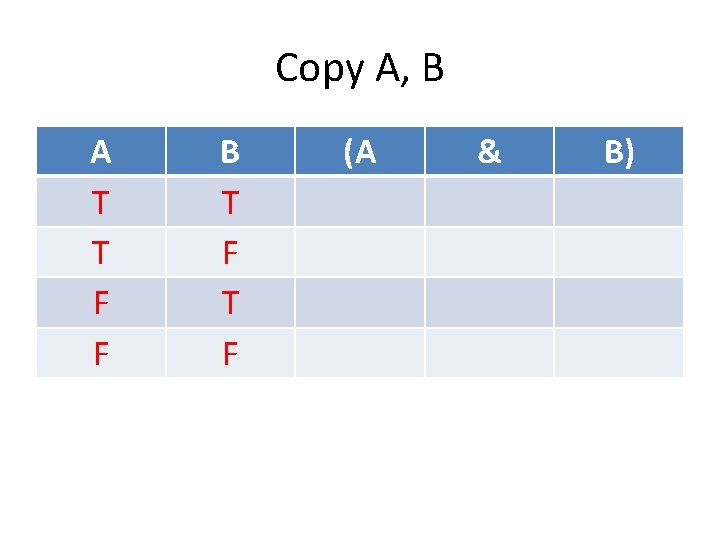
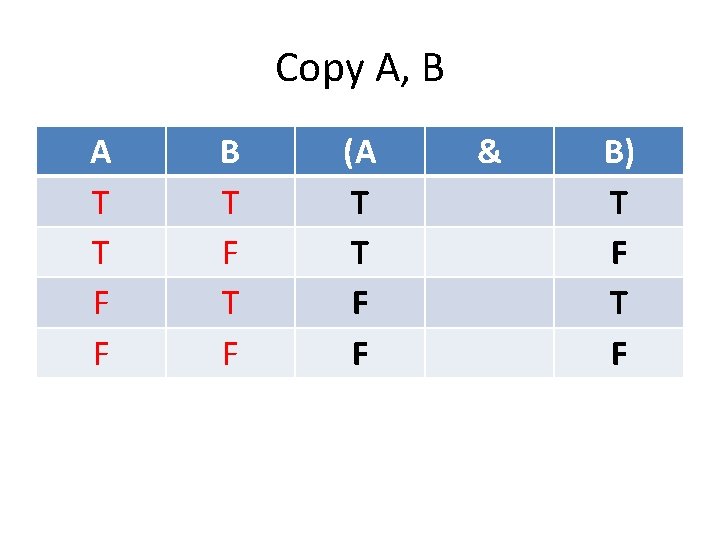
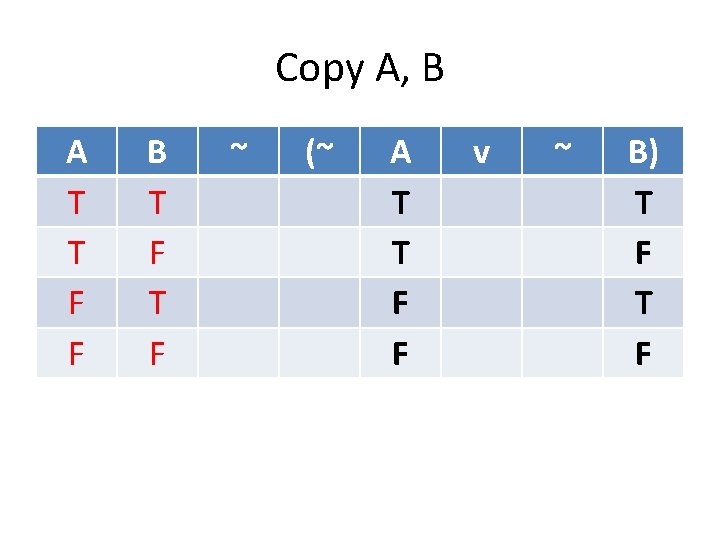
Copy A, B A T T F F B T F (A & B)

Copy A, B A T T F F B T F (A T T F F & B) T F

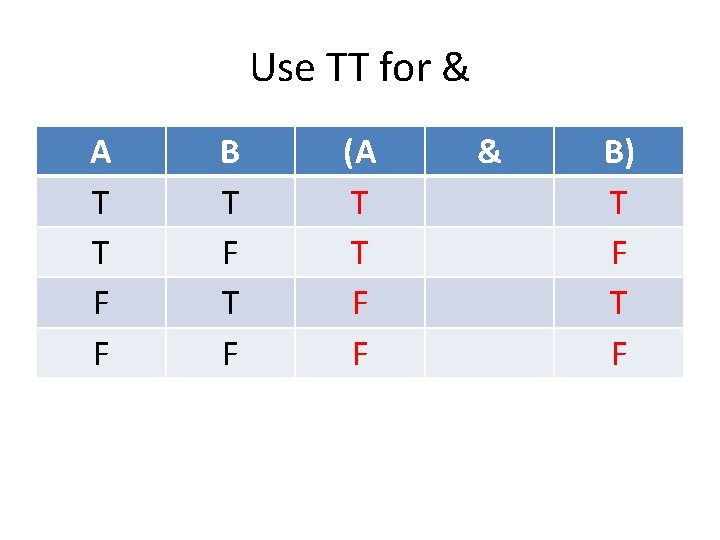
Use TT for & A T T F F B T F (A T T F F & B) T F

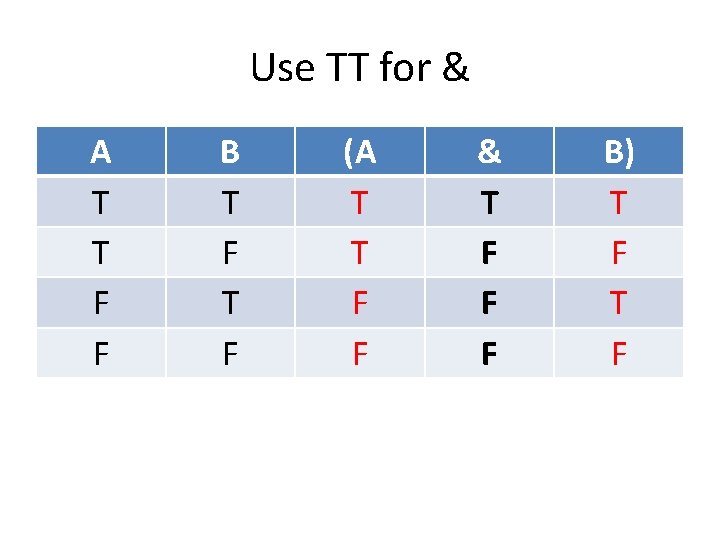
Use TT for & A T T F F B T F (A T T F F & T F F F B) T F

Now Make TT for ~(~A v ~B) A T T F F B T F ~ (~ A v ~ B)

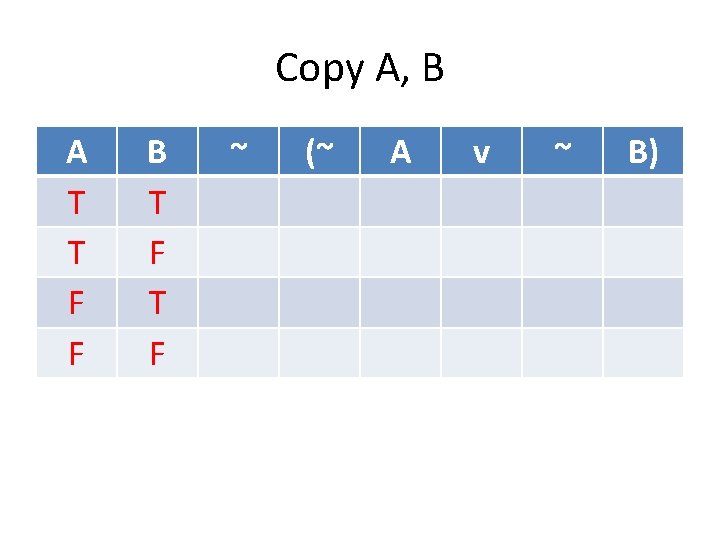
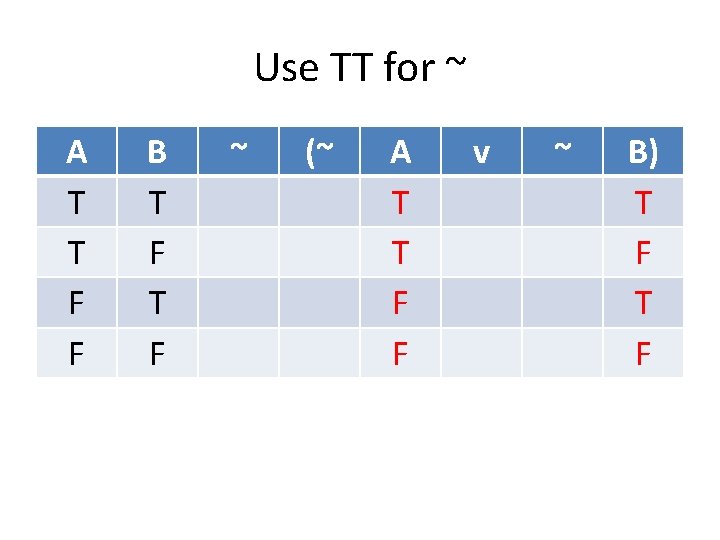
Copy A, B A T T F F B T F ~ (~ A v ~ B)

Copy A, B A T T F F B T F ~ (~ A T T F F v ~ B) T F

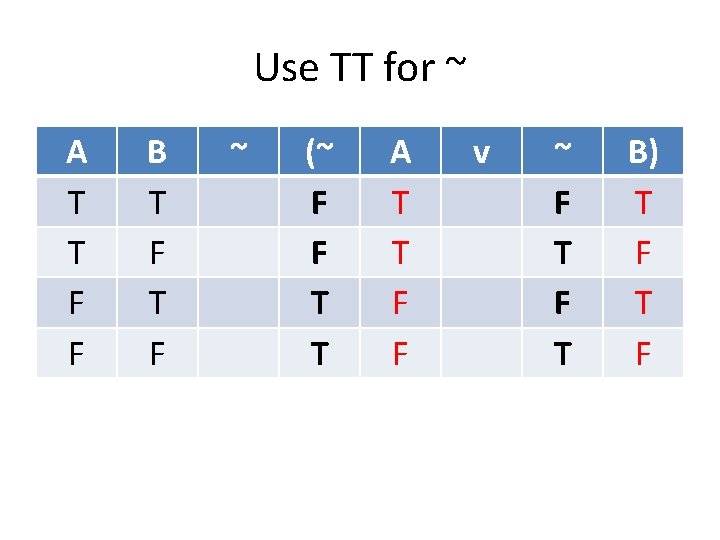
Use TT for ~ A T T F F B T F ~ (~ A T T F F v ~ B) T F

Use TT for ~ A T T F F B T F ~ (~ F F T T A T T F F v ~ F T B) T F

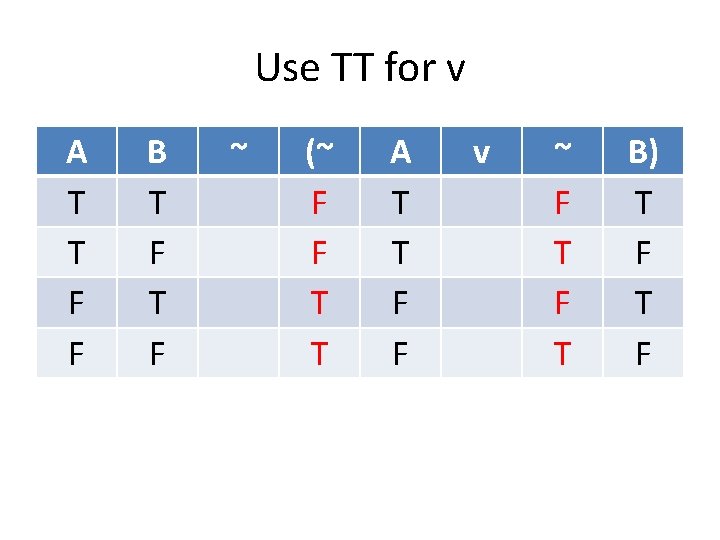
Use TT for v A T T F F B T F ~ (~ F F T T A T T F F v ~ F T B) T F

Use TT for v A T T F F B T F ~ (~ F F T T A T T F F v F T T T ~ F T B) T F

Use TT for ~ A T T F F B T F ~ (~ F F T T A T T F F v F T T T ~ F T B) T F

Use TT for ~ A T T F F B T F ~ T F F F (~ F F T T A T T F F v F T T T ~ F T B) T F

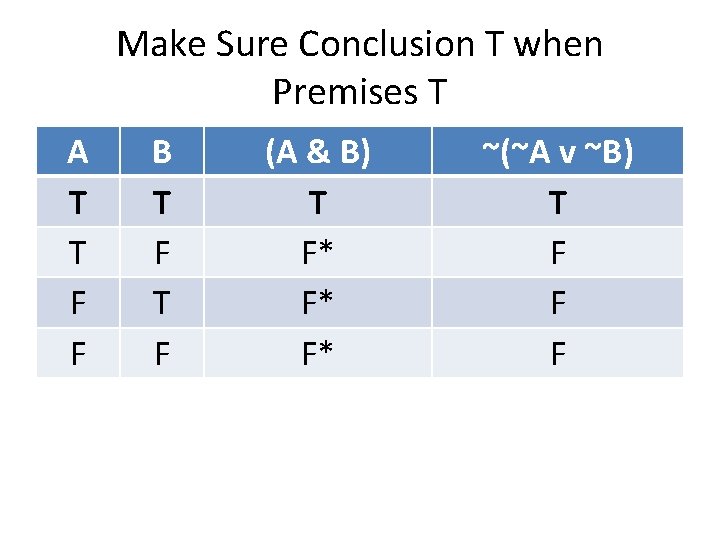
Truth-Table Test Now we can do the truth-table test for validity. Remember that an argument is valid when IF the premises are true, THEN the conclusion is true.

Write Down Possibilities A T T F F B T F

Write Down TT for Premises A T T F F B T F (A & B) T F F F

Write Down TT for Conclusion A T T F F B T F (A & B) T F F F ~(~A v ~B) T F F F

Make Sure Conclusion T when Premises T A T T F F B T F (A & B) T F* F* F* ~(~A v ~B) T F F F

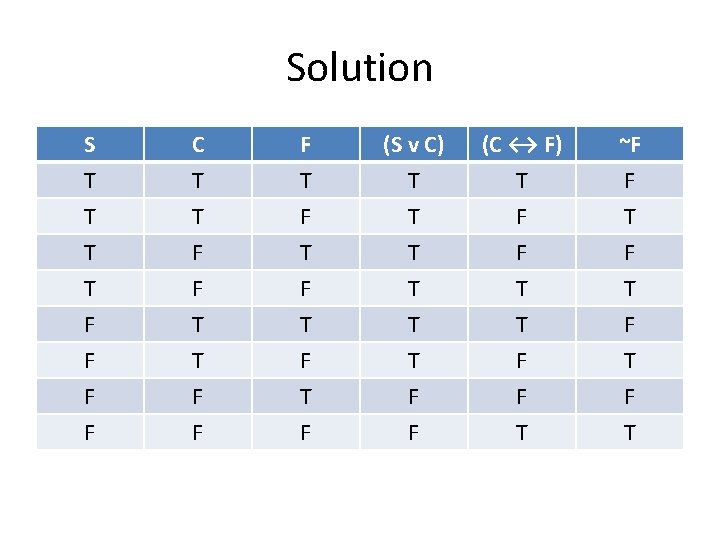
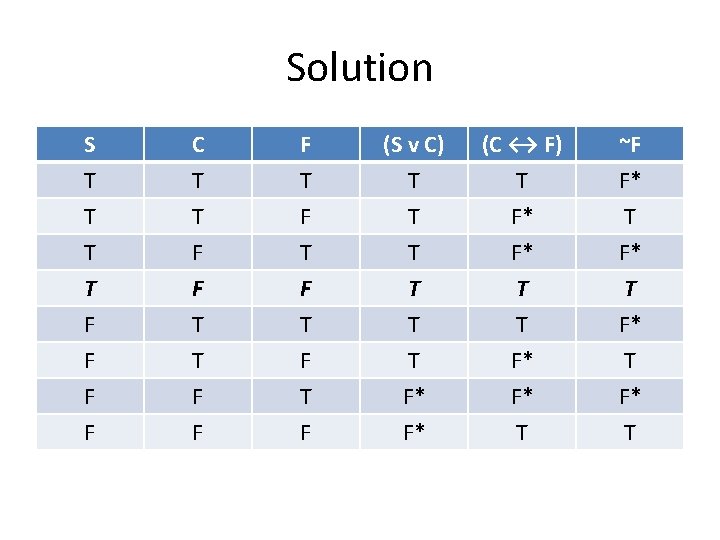
Consistency A set of sentences is consistent if all of the sentences can be true at the same time. (Some or all of them might in fact be false, but they all CAN be true together). A set of sentences is inconsistent if they CANNOT all be true at the same time.

Example Problem #3 Consider the following three sentences. 1. Sam will be sad unless we come to his party. 2. We will come to Sam’s party if and only if there is food. 3. Sam won’t have food at the party. Are they logically consistent all together?

Using SL Translate: S = Sam is sad C = We come to Sam’s party F = There is food at the party

Using SL Translate: 1. (S v C) 2. (C ↔ F) 3. ~F

Solution S T T T C T T F F T (S v C) T T T (C ↔ F) T F F ~F F T F F F T F T T T F F T T F T

Solution S T T T C T T F F T (S v C) T T T (C ↔ F) T F* F* ~F F* T F F F T F T T T F* F* T T F* T

Proofs I advise you to avoid the proofs unless you are already pretty confident about your ability to do them. Advance warning: the two optional proofs both involve using ~I or ~E. These rules are tricky, so if you plan on considering the proofs, commit them to memory.

~I (Negation Introduction) If you have assumed ψ, and you have derived (φ&~φ), then you can write down ~ψ, depending on everything (φ&~φ) depends on except ψ.

(P v P) ├ P 1 2 1, 2 2 1. (P v P) 2. ~P 3. P 4. (P & ~P) 5. P A A (for ~E) 1 v. E 2, 3 &I 2, 4 ~E

PREDICATE LOGIC

Predicate Logic on the Final There are fewer predicate logic questions on the final than SL questions. About 2 multiple choice and 2 short answer. So between 5% and 15% of your grade, depending on which questions you choose on the short answer.

What to Study • The lecture slides on predicate logic. • Joe Lau’s module on predicate logic, especially PL 02 Quantifiers. The predicate logic questions are surprisingly not as difficult as you would think, so studying PL is a good investment.

Equivalences I’d highly recommend committing to memory these very easy-to-remember logical equivalences: • ∀y. Dy ≡ ~∃y~Dy • ~∀y. Dy ≡ ∃y~Dy • ∀y~Dy ≡ ~∃y. Dy • ~∀y~Dy ≡ ∃y. Dy