Logic Representation and Inference Introduction to Semantics What

Logic, Representation and Inference Introduction to Semantics • What is semantics for? • Role of FOL • Montague Approach February 2009 Introduction to Semantics 1

Semantics • Semantics is the study of the meaning of NL expressions • Expressions include sentences, phrases, and sentences. • What is the goal of such study? – Provide a workable definition of meaning. – Explain semantic relations between expressions. February 2009 Introduction to Semantics 2

Examples of Semantic Relations • Synonymy – John killed Mary – John caused Mary to die • Entailment – John fed his cat – John has a cat • Consistency – John is very sick – John is not feeling well – John is very healthy February 2009 Introduction to Semantics 3

Different Kinds of Meaning X means Y • Meaning as definition: – a bachelor means an unmarried man • Meaning as intention: – What did John mean by waving? • Meaning as reference: "Eiffel Tower " means February 2009 Introduction to Semantics 4

Workable Definition of Meaning • Restrict the scope of semantics. • Ignore irony, metaphor etc. • Stick to the literal interpretations of expressions rather than metaphorical ones. (My car drinks petrol). • Assume that meaning is understood in terms of something concrete. February 2009 Introduction to Semantics 5

Concrete Semantics • Procedural semantics: the meaning of a phrase or sentence is a procedure: “Pick up a big red block” (Winograd 1972) • Object–Oriented Semantics: meaning is an instance of a class. • Truth-Conditional Semantics February 2009 Introduction to Semantics 6

Truth Conditional Semantics • Key Claim: the meaning of a sentence is identical to the conditions under which it is true. • Know the meaning of "Ġianni ate fish for tea" = know exactly how to apply it to the real world and decide whether it is true or false. • On this view, one task of semantic theory is to provide a system for identifying the truth conditions of sentences. February 2009 Introduction to Semantics 7

TCS and Semantic Relations • TCS provides a precise account of semantic relations between sentences. • Examples: – – S 1 is synonymous with S 2. S 1 entails S 2 S 1 is consistent with S 2. S 1 is inconsistent with S 2. • Just like logic! • Which logic? February 2009 Introduction to Semantics 8

NL Semantics: Two Basic Issues • How can we automate the process of associating semantic representations with expressions of natural language? • How can we use semantic representations of NL expressions to automate the process of drawing inferences? • We will focus mainly on first issue. February 2009 Introduction to Semantics 9

Associating Semantic Representations Automatically • • • Design a semantic representation language. Figure out how to compute the semantic representation of sentences Link this computation to the grammar and lexicon. February 2009 Introduction to Semantics 10

Semantic Representation Language • Logical form (LF) is the name used by logicians (Russell, Carnap etc) to talk about the representation of contextindependent meaning. • Semantic representation language has to encode the LF. • One concrete representation for logical form is first order logic (FOL) February 2009 Introduction to Semantics 11

Why is FOL a good thing? • Has a precise, model-theoretic semantics. • If we can translate a NL sentence S into a sentence of FOL, then we have a precise grasp on at least part of the meaning of S. • Important inference problems have been studied for FOL. Computational solutions exist for some of them. • Hence the strategy of translating into FOL also gives us a handle on inference. February 2009 Introduction to Semantics 12

Anatomy of FOL • Symbols of different types – – – – constant symbols: variable symbols: function symbols: predicate symbols: connectives: &, v, quantifiers: , punctuation: ), (, “, ” February 2009 a, b, c x, y, z f, g, h p, q, r Introduction to Semantics 13

Anatomy of FOL • Symbols of different types – – – – constant symbols: csa 3180, nlp, mike, alan, rachel, csai variable symbols: x, y, z function symbols: lecturer. Of, subject. Of predicate symbols: studies, likes connectives: &, v, quantifiers: , punctuation: ), (, “, ” February 2009 Introduction to Semantics 14

Anatomy of FOL With these symbols we can make expressions of different types – Expressions for referring to things • constant: • variable: • term: alan, nlp x subject(csa 3180) – Expressions for stating facts • atomic formula: study(alan, csa 3180) • complex formula: study(alan, csa 3180) & teach(mike, csa 3180) • quantified expression: x y teaches(lecturer(x), x) & studies(y, subject(x)) x y likes(x, subject. Of(y)) studies(x, y) February 2009 Introduction to Semantics 15

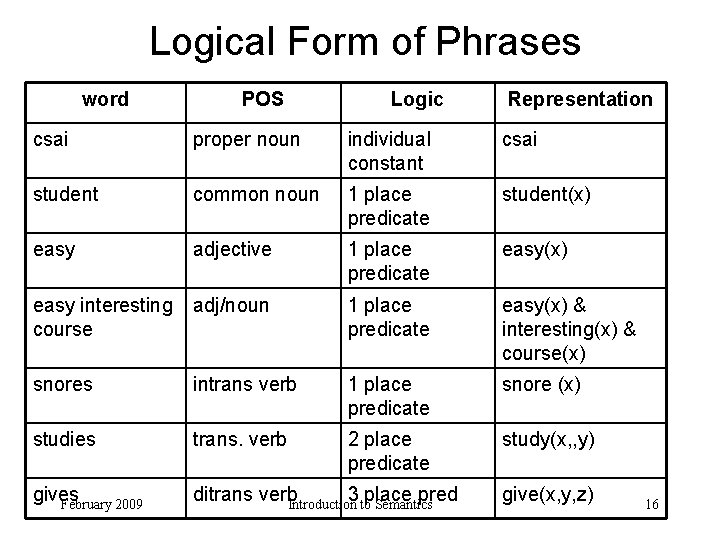
Logical Form of Phrases word POS Logic Representation csai proper noun individual constant csai student common noun 1 place predicate student(x) easy adjective 1 place predicate easy(x) easy interesting course adj/noun 1 place predicate easy(x) & interesting(x) & course(x) snores intrans verb 1 place predicate snore (x) studies trans. verb 2 place predicate study(x, , y) gives February 2009 ditrans verb. Introduction 3 toplace pred Semantics give(x, y, z) 16

Logical Forms of Sentences • John kicks Fido: kick(john, fido) • Every student wrote a program x y( stud(x) prog(y) & write(x, y)) y x(stud(x) prog(y) & write(x, y)) • Semantic ambiguity related to quantifier scope February 2009 Introduction to Semantics 17

Building Logical Form Frege’s Principle of Compositionality • The POC states that the LF of a complex phrase can be built out of the LFs of the constituent parts. • An everyday example of compositionality is the way in which the “meaning” of arithmetic expressions is computed (2+3) * (4/2) = (5 * 2) = 10 February 2009 Introduction to Semantics 18

Compositionality for NL • The LF of the whole sentence can be computed from the LF of the subphrases, i. e. • Given the syntactic rule X Y Z. • Suppose [Y], [Z] are the LFs of Y, and Z respectively. • Then [X] = ([Y], [Z]) where is some function for semantic combination February 2009 Introduction to Semantics 19

Claims of Richard Montague: • Each syntax rule is associated with a semantic rule that describes how the LF of the LHS category is composed from the LF of its subconstituents • 1: 1 correspondence between syntax and semantics (rule-to-rule hypothesis) • Functional composition proposed for combining semantic forms. • Lambda calculus proposed as the mechanism for describing functions for semantic combination. February 2009 Introduction to Semantics 20

Sentence Rule • Syntactic Rule: S NP VP • Semantic Rule: [S] = [VP]([NP]) i. e. the LF of S is obtained by "applying" the LF of VP to the LF of NP. • For this to be possible [VP] must be a function, and [NP] the argument to the function. February 2009 Introduction to Semantics 21

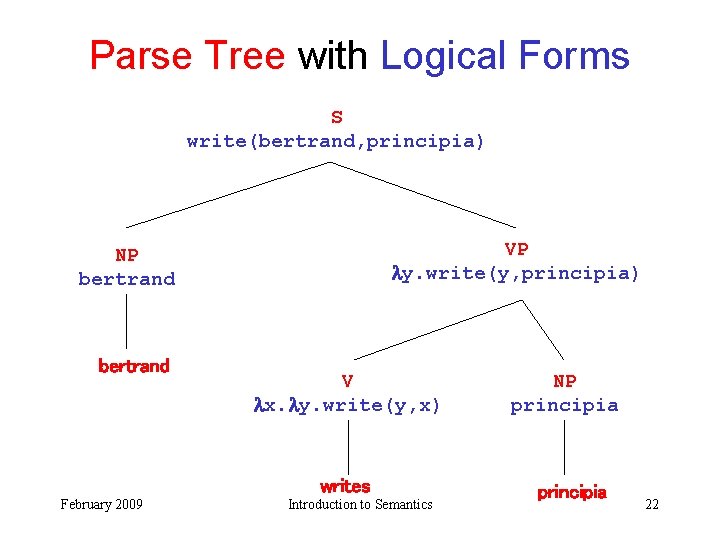
Parse Tree with Logical Forms S write(bertrand, principia) VP y. write(y, principia) NP bertrand V x. y. write(y, x) writes February 2009 Introduction to Semantics NP principia 22