Logic Programming Some declarative slides on logic programming

Logic Programming Some "declarative" slides on logic programming and Prolog. James Brucker

Introduction to Logic Programming q q Declarative programming describes what is desired from the program, not how it should be done Declarative language: statements of facts and propositions that must be satisfied by a solution to the program real(x). proposition: x is a real number. x > 0. proposition: x is greater than 0.

Declarative Languages q q what is a "declarative language? " give another example (not Prolog) of a declarative language. SELECT * FROM COUNTRY WHERE CONTINENT = 'Asia';

Facts, Rules. . . , q What is a proposition? q What are facts? q What are rules? q What is a predicate? q What is a compound term?

Facts: fish(salmon). likes(cat, tuna). Predicates: fish, likes Compound terms: likes(cat, X), fish(X) Atoms: cat, salmon, tuna Rule: eats(cat, X) likes(cat, X), fish(X).

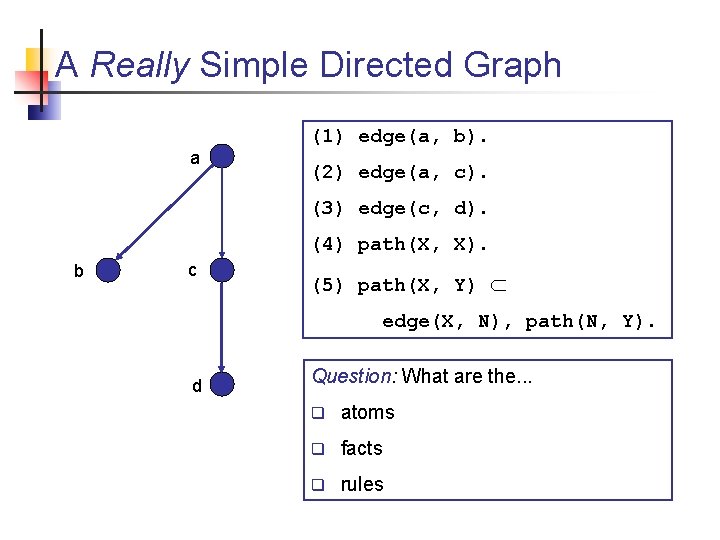
A Really Simple Directed Graph a (1) edge(a, b). (2) edge(a, c). (3) edge(c, d). (4) path(X, X). b c (5) path(X, Y) edge(X, N), path(N, Y). d Question: What are the. . . q atoms q facts q rules

Clausal Form q q Problem: There are too many ways to express propositions. n difficult for a machine to parse or understand Clausal form: standard form for expressing propositions Consequent Antecedent Example: path(X, Y) edge(X, N) path(N, Y).

Clausal Form Example path(X, Y) edge(X, N) path(N, Y). Meaning: if there is an edge from X to N and there a path from N to Y, then there is a path from X to Y. The above is also called a "headed Horn clause". In Prolog this is written as a proposition or rule: path(X, Y) : - edge(X, N) , path(N, Y).

Query A query or goal is an input proposition that we want Prolog to "prove" or disprove. q A query may or may not require that Prolog give us a value that satisfies the query (instantiation). q 1 ? - edge(a, b). Yes 2 ? - path(c, b). No 3 ? - path(c, X). X = c ; X = d ; No

Logical Operations on Propositions q What are the two operations that a logic programming language performs on propositions to establish a query? That is, how does it satisfy a query, such as:

Unification is a process of finding values of variables (instantiation) to match terms. Uses facts. (1 -3) edge(a, b). edge(a, c). edge(c, d). (Facts) (4) path(X, X). (Rule) (5) path(X, Y) : = edge(X, N), path(N, Y). (Rule) ? - path(a, d). This is the query (goal). Instantiate { X=a, Y=d }, and unify path(a, d) with Rule 5. After doing this, Prolog must satisfy: edge(a, N). This is a subgoal. path(N, d). This is a subgoal.

Unification in plain English Compare two atoms and see if there is a substitution which will make them the same. 1. edge(a, b). (Fact) 5. path(X, Y) : - edge(X, N) , path(N, Y). 6. path(a, Z). How can we unify 6 with 5? Let X : = a Let Y : = Z (Query)

Resolution is an inference rule that allows propositions to be combined. q Idea: match the consequent (LHS) of one proposition with the antecedent (RHS term) of another. q Examples are in the textbook and tutorials.

Resolution Example 1. edge(a, b). (Fact) 5. path(X, Y) : - edge(X, N) , path(N, Y). 6. path(a, Z). How can we unify 6 with 5? Let X : = a Let Y : = Z Resolution: (Query)

Resolution is an inference rule that allows propositions to be combined. q Idea: match the consequent (LHS) of one proposition with the antecedent (RHS term) of another. q Examples are in the textbook and tutorials.

How to handle failures q Prolog can work backwards towards the facts using resolution, instantiation, and unification. q As it works, Prolog must try each of several choices. q These choices can be stored as a tree. ? - path(a, d). The goal. Unify: unify path(a, d)with Rule 5 by instantiate { X=a, Y=d } Subgoal: edge(a, N). Instantiate: N=b which is true by Fact 1. Subgoal: path(b, d). Unify: path(b, d)with Rule 5: path(b, d) : - edge(b, N), path(N, d) Failure: can't instantiate edge(b, N) using any propositions.

How to handle failures (2( q q When a solution process fails, Prolog must undo some of the decisions it has made. This is called backtracking. n q same as backtracking you use in recursion. Marks a branch of the tree as failed.

How it Works (1( There are 2 search/execution strategies that can be used by declarative languages based on a database of facts. q 1. Forward Chaining 2. Backward Chaining what are the meanings of these terms?

How it Works (2( q q 1. Forward Chaining 2. Backward Chaining Which strategy does Prolog use? Under what circumstances is one strategy more effective than the other? Consider two cases: n large number of rules, small number of facts n small number of rules, large number of facts

PROLOG: PROgramming in LOGic The only "logic" programming language in common use.

3 Parts of a Prolog Program 1. A database contains two kinds of information. § What information is in a database? 2. A command to read or load the database. § in Scheme you can use load("filename") § in Prolog use consult('filename') 3. A query or goal to solve.

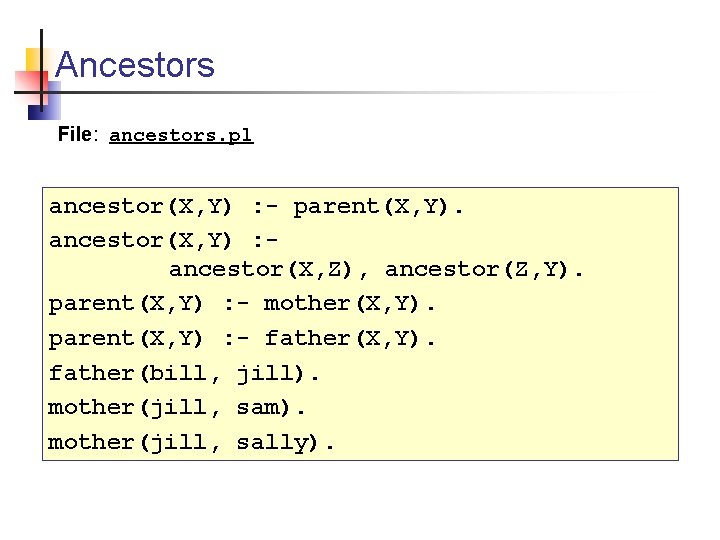
Ancestors File: ancestors. pl ancestor(X, Y) : - parent(X, Y). ancestor(X, Y) : ancestor(X, Z), ancestor(Z, Y). parent(X, Y) : - mother(X, Y). parent(X, Y) : - father(X, Y). father(bill, jill). mother(jill, sam). mother(jill, sally).

Query the Ancestors ? - consult('/pathname/ancestors. pl'). ancestor(bill, sam). Yes ? - ancestor(bill, X). X = jill ; X = sam ; ERROR: Out of local stack ? - ancestor(X, bob). ERROR: Out of local stack

Understanding the Problem q You need to understand how Prolog finds a solution. ancestor(X, Y) : - parent(X, Y). ancestor(X, Y) : ancestor(X, Z), ancestor(Z, Y). parent(X, Y) : - mother(X, Y). parent(X, Y) : - father(X, Y). father(bill, jill). mother(jill, sam). father(bob, sam). Depth-first search causes immediate recursion

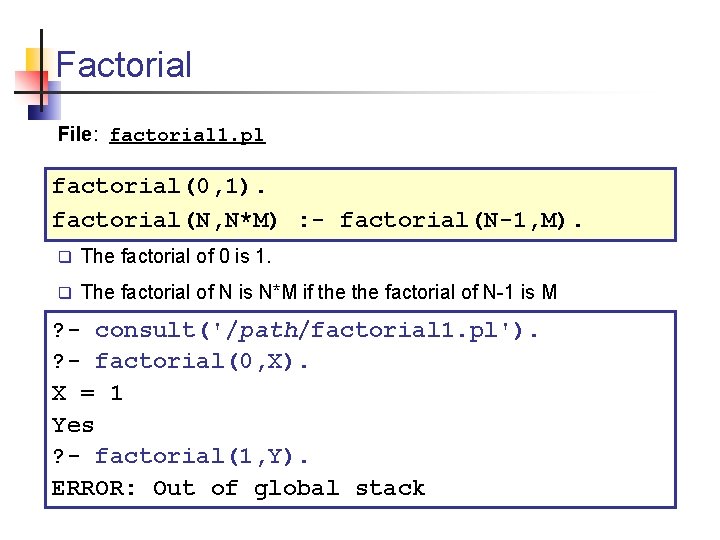
Factorial File: factorial 1. pl factorial(0, 1). factorial(N, N*M) : - factorial(N-1, M). q The factorial of 0 is 1. q The factorial of N is N*M if the factorial of N-1 is M ? - consult('/path/factorial 1. pl'). ? - factorial(0, X). X = 1 Yes ? - factorial(1, Y). ERROR: Out of global stack

Query Factorial ? - consult('/path/factorial 1. pl'). ? - factorial(2, 2). No ? - factorial(1, X). ERROR: Out of global stack Problem: Arithmetic is not performed automatically. ? - 2*3 = 6. No ? - 2*3 = 2*3. Yes ? - 6 is 2*3. is(6, 2*3). Yes ? - 2*3 is 6. No l-value = r-value ?

Arithmetic via Instantiation: is q q "=" simply means comparison for identity. factorial(N, 1) : - N=0. "is" performs instantiation if the left side doesn't have a value yet. product(X, Y, Z) : - Z is X*Y. n n this rule can answer the query: product(3, 4, N). Answer: N = 12. but it can't answer: product(3, Y, 12).

is does not mean assignment! q This always fails: N is N - 1. % sumto(N, Total): compute Total = 1 + 2 +. . . + N. sumto(N, 0) : - N =< 0. sumto(N, Total) : = Total is Subtotal + N, N is N-1, always fails sumto(N, Subtotal). ? - sumto(0, Sum). Sum = 0. Yes ? - sumto(1, Sum). No

is : how to fix? q How would you fix this problem? % sumto(N, Total): compute Total = 1 + 2 +. . . + N. sumto(N, 0) : - N =< 0. sumto(N, Total) : = N 1 is N-1, sumto(N 1, Subtotal), Total is Subtotal + N. ? = sumto(5, X). always fails

Factorial revised File: factorial 2. pl factorial(0, 1). factorial(N, P) : - N 1 is N-1, factorial(N 1, M), P is M*N. Meaning: q The factorial of 0 is 1. q factorial of N is P if N 1 = N-1 and factorial of N 1 is M and P is M*N.

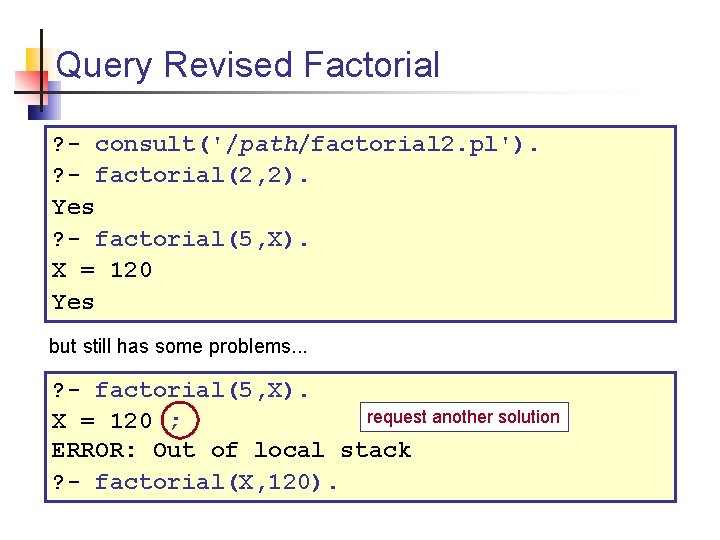
Query Revised Factorial ? - consult('/path/factorial 2. pl'). ? - factorial(2, 2). Yes ? - factorial(5, X). X = 120 Yes but still has some problems. . . ? - factorial(5, X). request another solution X = 120 ; ERROR: Out of local stack ? - factorial(X, 120).

Factorial revised again File: factorial 3. pl Makes the rules mutually exclusive. factorial(0, 1). factorial(N, P) : - not(N=0), N 1 is N-1, factorial(N 1, M), P is M*N. ? - factorial(5, X). X = 120 ; No ? -

Readability: one clause per line factorial(0, 1). factorial(N, P) : - not(N=0), N 1 is N-1, factorial(N 1, M), P is M*N. factorial(0, 1). factorial(N, P) : not(N=0), N 1 is N-1, factorial(N 1, M), P is M*N. Better

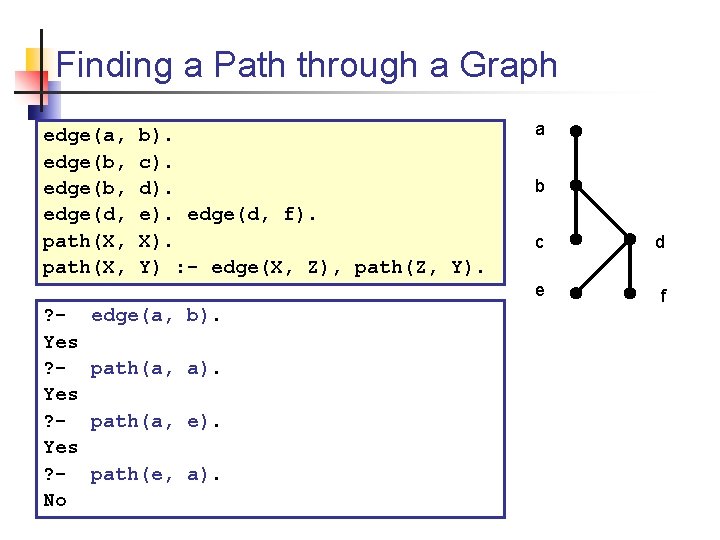
Finding a Path through a Graph edge(a, edge(b, edge(d, path(X, ? Yes ? No b). c). d). edge(d, f). X). Y) : - edge(X, Z), path(Z, Y). edge(a, b). path(a, a). path(a, e). path(e, a). a b c d e f

How To Define an Undirected Graph? edge(a, edge(b, edge(d, edge(X, path(X, b). c). d). e). f). Y) : = not(X=Y), edge(Y, X). Y) : - edge(X, Z), path(Z, Y). ? - edge(b, a). Yes ? - path(a, b). Yes ? - path(b, e). No a b c d e f

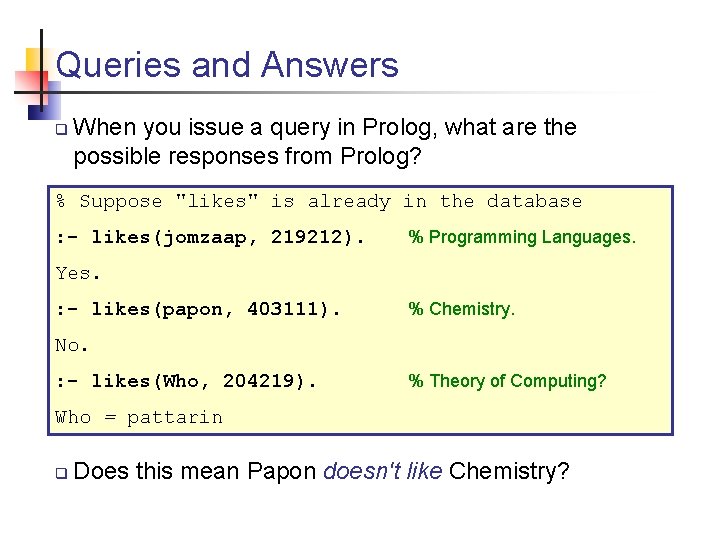
Queries and Answers q When you issue a query in Prolog, what are the possible responses from Prolog? % Suppose "likes" is already in the database : - likes(jomzaap, 219212). % Programming Languages. Yes. : - likes(papon, 403111). % Chemistry. No. : - likes(Who, 204219). % Theory of Computing? Who = pattarin q Does this mean Papon doesn't like Chemistry?

Closed World Assumption q q What is the Closed World Assumption? How does this affect the interpretation of results from Prolog?

List Processing ]Head | Tail] works like "car" and "cdr" in Scheme. q Example: q ? - [H | T ] = [a, b, c, d, e]. returns: H = a T = [b, c, d, e] This can be used to build lists and decompose lists. q Can use [H|T] on the left side to de/construct a list: q path(X, Y, [X|P]) : edge(X, Node), path(Node, Y, P).

member Predicate q Test whether something is a member of a list ? - member(a, [b, c, d]). No. q can be used to have Prolog try all values of a list as values of a variable. ? - member(X, [a 1, b 2, c 3, d 4] ). X = a 1 X = b 2 X = c 3

member Predicate example q q Use member to try all values of a list. Useful for problems like n Queen safety n enumerating possible rows and columns in a game. % dumb function to find square root of 9 squareroot 9(N) : member(N, [1, 2, 3, 4, 5, 5, 6, 7, 8, 9]), 9 is N*N.

appending Lists ? - append([a, b], [c, d, e], L). L = [a, b, c, d, e] ? - append([], [a, b, c], L). L = [a, b, c] q append can resolve other parameters, too: ? - append(X, [b, c, d], [a, b, c, d] ). X = a

Defining your own 'append' append([], List). append([Head|Tail], X, [Head|New. Tail]) : append(Tail, X, New. Tail).

Type Determination Prolog is a weakly typed language. q It provides propositions for testing the type of a variable q PREDICATE SATISFIED (TRUE) IF var(X) X is a variable nonvar(X) X is not a variable atom(A) A is an atom integer(K) K is an integer real(R) R is a floating point number(N) N is an integer or real atomic(A) A is an atom or a number or a string functor(T, F, A) T is a term with functor F, arity A T =. . L T is a term, L is a list. clause(H, T) H : - T is a rule in the program

Tracing the Solution ? - trace. [trace] ? - path(a, d). Call: (8) path(a, d) ? creep Call: (9) edge(a, _L 169) ? creep Exit: (9) edge(a, b) ? creep Call: (9) path(b, d) ? creep Call: (10) edge(b, _L 204) ? creep Exit: (10) edge(b, c) ? creep Call: (10) path(c, d) ? creep Call: (11) edge(c, _L 239) ? creep ^ Call: (12) not(c=_G 471) ? creep ^ Fail: (12) not(c=_G 471) ? creep Fail: (11) edge(c, _L 239) ? creep Fail: (10) path(c, d) ? creep Redo: (10) edge(b, _L 204) ? creep

Solution Process (1) path(X, X). (2) path(X, Y) : = edge(X, Z), path(Z, Y). ? - path(a, c). Stack Substitution (Instantiation) [path(a, c), path(X, X)] [path(a, c), path(a, a)] X=a Undo. [path(a, c), path(X, X)] [path(a, c), path(c, c)]X = c Undo.

Solution Process (2( (1) path(X, X). (2) path(X, Y) : = edge(X, Z), path(Z, Y). ? - path(a, c). Stack Substitution (Instantiation) [path(a, c), path(X, Y)] (Rule 2) [path(a, c), path(a, Y)] X=a X = a, Y = c edge(a, Z), path(Z, c) new subgoals edge(a, b), path(b, c) X = a, Y = c, Z = b path(b, c) edge(a, b) is a fact - pop it.

What does this do? % what does this do? sub([], List). sub([H|T], List) : member(H, List), sub(T, List).

What does this do? Underscore (_) means "don't care". % what does this do? It accepts any value. foo([], _, []). foo([H|T], List, [H|P]) : member(H, List), foo(T, List, P). foo([H|T], List, P) : not( member(H, List) ), foo(T, List, P).

Max Function q q Write a Prolog program to find the max of a list of numbers: n max( List, X). n max( [3, 5, 8, -4, 6], X). X = 8. Strategy: n use recursion n divide the list into a Head and Tail. n compare X to Head and Tail. Two cases: n n n Head = max( Tail ). in this case answer is X is Head. X = max( Tail ) and Head < X. what is the base case?

Max Function % max(List, X) : X is max of List members max([X], X). base case max([H|Tail], H) : - 1 st element is max(Tail, X), H >= X. max([H|Tail], X) : complete this case. 1 st element not max

Towers of Hanoi % Move one disk move(1, From, To, _) : write('Move top disk from '), write(From), write(' to '), See tutorials at: write(To), www. csupomona. edu and nl. www. cse. ucsc. edu % Move more than one disk. move(N, From, To, Other) : N>1, M is N-1, move(M, From, Other, To), move(1, From, To, _), move(M, Other, To, From).

Learning Prolog q The Textbook - good explanation of concepts q Tutorials: n n http: //www. thefreecountry. com/documentation/onlineprolog. sht ml has annotated links to tutorials. http: //www. cse. ucsc. edu/classes/cmps 112/Spring 03/language s/prolog/Prolog. Intro. pdf last section explains how Prolog resolves queries using a stack and list of substitutions. http: //cs. wwc. edu/~cs_dept/KU/PR/Prolog. html explains Prolog syntax and semantics. http: //www. csupomona. edu/~jrfisher/www/prolog_tutorial/conte nts. html has many examples