Logic Programming Robert Kowalskis equation Algorithm Logic Control

Logic Programming • Robert Kowalski’s equation: Algorithm = Logic + Control • Definite logic program: A B 1, B 2, …, Bm (program clause) head body A 1, A 2, …, An (goal clause) 1

Logic Programming • SLD-resolution: Ø Resolvent: A 1, …, Ak-1, Ak+1, …, An A B 1, B 2, …, Bm (A 1, …, Ak-1, B 2, …, Bm, Ak+1, …, An) Ak = A SL-resolution for Definite clauses - SL = Linear resolution with Selection function 2

Logic Programming • SLD-resolution: Ø SLD-derivation: G 0 = G, G 1, G 2, …, Gn C 1, C 2, …, Cn 1, 2, …, n (mgu’s) i+1 Ci+1 = i+1 Gi Ø SLD-refutation: Gn = empty Ø Computed answer: n… 2 1 3

Logic Programming • SLD-resolution: Ø Soundness: if n… 2 1 is a computed answer, then P |= n… 2 1 G Ø Completeness: if P |= G, then there exists a computed answer s such that = s for some Example: p(X, Z) q(X, Y), p(Y, Z) p(X, X) q(a, b) 4

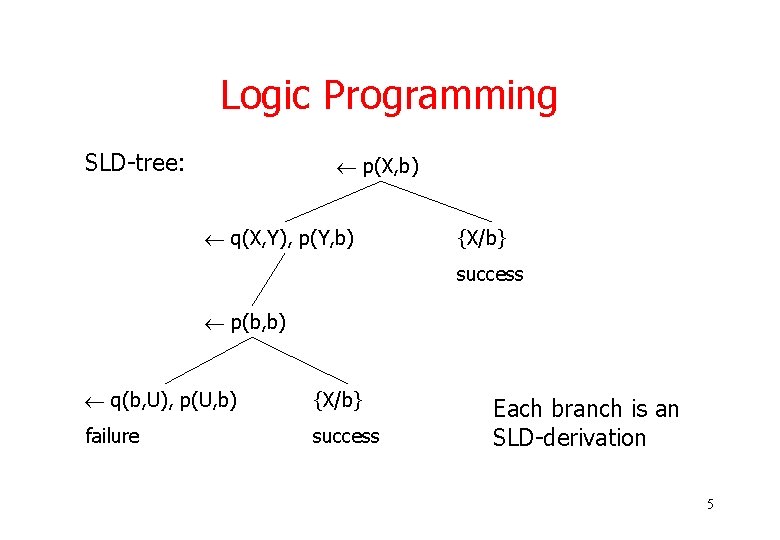
Logic Programming SLD-tree: p(X, b) q(X, Y), p(Y, b) {X/b} success p(b, b) q(b, U), p(U, b) {X/b} failure success Each branch is an SLD-derivation 5

Logic Programming • PROLOG (Alain Colmerauer 1972): Ø Only Horn sentences are acceptable Ø The occur-check is omitted from the unification unsound Example: test p(X, X) p(X, f(X)) Ø Backward chaining with depth-first search incomplete Example: p(X, Y) q(X, Y) p(X, X) q(X, Y) q(Y, X) 6

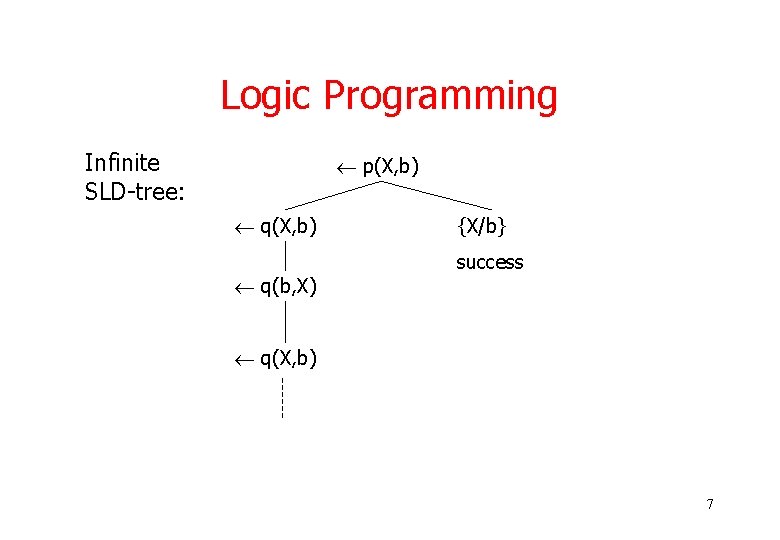
Logic Programming Infinite SLD-tree: p(X, b) q(b, X) {X/b} success q(X, b) 7

Logic Programming • PROLOG (Alain Colmerauer 1972): Ø Unsafe cut incomplete Example: A B, C B D, !, E D A B, C D, !, E, C Ø Negation as failure: P if fails to prove P 8

Theorem Provers • Accepts full first-order logic • Keeps control distinct from logic A B C A C B 9

Production Systems • Working memory: contains a set of positive literals with no variables • Rule memory: contains a set of reference rules of the form p 1 p 2 … act 1 act 2 … pi are literals acti are actions to delete or add elements to the working memory 10

Production Systems • Forwarding chaining in each cycle: Ø Match phase: computes the subset of rules whose left-hand side is satisfied by the current contents of the working memory Ø Conflict resolution phase: decides which of the rules to be executed Ø Act phase: executes the actions in the chosen rules 11

Production Systems • Example: Ø Working memory: {A(1), A(2), B(3), B(4), C(5)} Ø Rule memory: A(x) B(x) C(y) add D(x) A(x) B(y) D(x) add E(x) A(x) B(x) E(x) delete A(x) 12

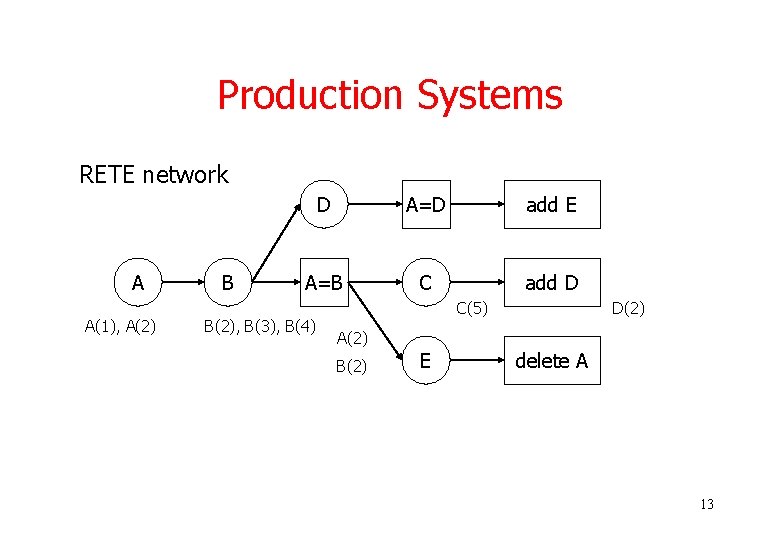
Production Systems RETE network A A(1), A(2) B D A=D add E A=B C add D B(2), B(3), B(4) C(5) D(2) A(2) B(2) E delete A 13

Exercises • In Russell & Norvig’s AIMA (Chapter 10): 10. 2, 10. 4 14