Logic Programming contd Lists in Prolog are represented

Logic Programming (cont’d): Lists in Prolog are represented by a functor (similar to cons in Scheme): 1. The empty list is represented by the constant - [ ]. 2. The term. (X , Xs) represents a list of which X is the 1 st element and Xs is the rest of its elements. 3. The functor ‘. ’ has an infix representation by the pipe symbol ‘|’ : [X | Xs] For example: [3 | [5 | [] ] ] 4. Lists of known length can be represented as a list of comma-separated expressions: For example: [ X, 2, f(Y) ] or [3 , 5]

Logic Programming (cont’d): Lists Example 1: Implementing a Context Free Grammar in PROLOG: S NP VP Det N V NP | V a | the woman | man saw Q: What language does this CFG represent? ? - s([a, woman, saw, a, man]). true ? -s(X). X = [the, woman, saw, the, woman]; X = [the, woman, saw, the, man]; X = [the, woman, saw, a, woman]; X = [the, woman, saw, a, man]; X = [the, woman, saw] … ? -s([the, man|X]). X = [saw, the, woman]; X = [saw, the, man]; X = [saw, a, woman] … Representation in PROLOG: s(Z) : - np(X), vp(Y), append(X, Y, Z). np(Z): - det(X), n(Y), append(X, Y, Z). vp(Z): - v(X), np(Y), append(X, Y, Z). vp(Z): - v(Z). det([the]). det([a]). n([woman]). n([man]). v([saw]).

Logic Programming (cont’d): Lists Example 1: Implementing a Context Free Grammar in PROLOG: S NP Adj VP Det N V NP VP Det N | Det Adj N vicious | marvelous V NP | V a | the woman | man saw Q: How would we implement the modifications above? Representation in PROLOG: s(Z) : - np(X), vp(Y), append(X, Y, Z). np(Z): - det(X), n(Y), append(X, Y, Z). np(Z): - det(X), adj(W), n(Y), append([X, W, Y], Z). vp(Z): - v(X), np(Y), append(X, Y, Z). vp(Z): - v(Z). adj([vicious]). adj([marvelous]). det([the]). det([a]). vp(Z): - v(X), np(Y), append(X, Y, Z). vp(Z): - v(Z). n([woman]). n([man]). det([the]). det([a]). v([shoots]). n([woman]). n([man]). v([shoots]).

Logic Programming (cont’d): Lists Example 2: Determining the order of specific times o In logic programming, symbols have no values: ‘ 2’ and ‘ 9’ are names and not numbers. o We cannot use the < relation to compare the order of numbers (it is infinite!). o However, a finite ordered relation may be represented by positions in lists. We would like to implement an ordered relation between pairs of the form (hour, weekday). % Type: Hour. % Constructor: functor h/1. % Signature: h(Hour)/1 % Example: h(18). % Identifier: is_hour/1 % Set of elements: hour_list/1 % Order: hour_order/2 % Type: Weekday. % Constructor: functor d/1. % Signature: d(Weekday)/1 % Example: d(Tue). % Identifier: is_weekday/1 % Set of elements: weekday_list/1 % Order: weekday_order/2

Logic Programming (cont’d): Lists Example 2: Determining the order of specific times o In logic programming, symbols have no values: ‘ 2’ and ‘ 9’ are names and not numbers. o We cannot use the < relation to compare the order of numbers (it is infinite!). o However, a finite ordered relation may be represented by positions in lists. We would like to implement an ordered relation between pairs of the form (hour, weekday). % Signature: hour_list(List)/1 % Purpose: Holds the ordered list of days hours. hour_list([h(0), h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8), h(9), h(10), h(11), h(12), h(13), h(14), h(15), h(16), h(17), h(18), h(19), h(20), h(21), h(22), h(23)]). % Signature: weekday_list(List)/1 % Purpose: Holds the ordered list of week days. weekday_list([d('Sun'), d('Mon'), d('Tue'), d('Wed'), d('Thu'), d('Fri'), d('Sat')]).

Logic Programming (cont’d): Lists Example 2: Determining the order of specific times hour_list([h(0), h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8), h(9), h(10), h(11), h(12), h(13), h(14), h(15), h(16), h(17), h(18), h(19), h(20), h(21), h(22), h(23)]). weekday_list([d('Sun'), d('Mon'), d('Tue'), d('Wed'), d('Thu'), d('Fri'), d('Sat')]). A predicate to identify hours: % Signature: is_hour? (Hour)/1 % Purpose: Succeeds iff Hour is an hour of the weekday. is_hour(h(H)) : - hour_list(Hour_list), member(h(H), Hour_list). An order relation between hours: % Signature: hour_order(H 1, H 2)/2 % Purpose: hour H 1 precedes the hour H 2 in some weekday. hour_order(h(H 1), h(H 2)) : - is_hour(h(H 1)), is_hour(h(H 2)), hour_list(Hour_list), precedes(h(H 1), h(H 2), Hour_list).

Logic Programming (cont’d): Lists Example 2: Determining the order of specific times hour_list([h(0), h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8), h(9), h(10), h(11), h(12), h(13), h(14), h(15), h(16), h(17), h(18), h(19), h(20), h(21), h(22), h(23)]). weekday_list([d('Sun'), d('Mon'), d('Tue'), d('Wed'), d('Thu'), d('Fri'), d('Sat')]). A predicate to identify weekdays: % Signature: is_weekday? (Day)/1 % Purpose: Success iff Weekday is a weekday of the week. is_weekday? (d(D)) : - weekday_list(Weekday_list), member(d(D), Weekday_list). An order relation between weekdays: % Signature: weekday_order(Weekday 1, Weekday 2)/2 % Purpose: Weekday 1 precedes weekday 2 % in some weekday_LT(d(D 1), d(D 2)) : - is_weekday(d(D 1)), is_weekday(d(D 2)), weekday_list(Weekday_list), precedes(d(D 1), d(D 2), Weekday_list).

Logic Programming (cont’d): Lists Example 2: Determining the order of specific times % Type: Time. % Signature: time(Hour, Week. Day)/2 % Example: time(h(18), d(Tue)). A predicate to identify times: % Signature: is_time? (Time)/1 % Purpose: Succeeds iff Time is an hour of some weekday. % Example: ? – is_time? (time(h(1), d(‘Sun’))). true. is_time? (time(h(H), d(D))) : - is_hour? (h(H)), is_weekday? (d(D)). An order relation between times: % Signature: time_LT(T 1, T 2)/2 % Purpose: The time T 1 precedes the time T 2 in the week. % Example: ? - time_order(time(h(5), d(‘Mon’)), time(h(1), d(‘Tue’)). % true. time_order(time(h(H 1), d(D 1)), time(h(H 2), d(D 2))) : - is_time(h(H 1), d(D 1))), is_time(h(H 2), d(D 2))), weekday_order(d(D 1), d(D 2)). time_order(time(h(H 1), d(D)), time(h(H 2), d(D))) : - is_time(h(H 1), d(D))), is_time(h(H 2), d(D))), hour_order(h(H 1), h(H 2)).

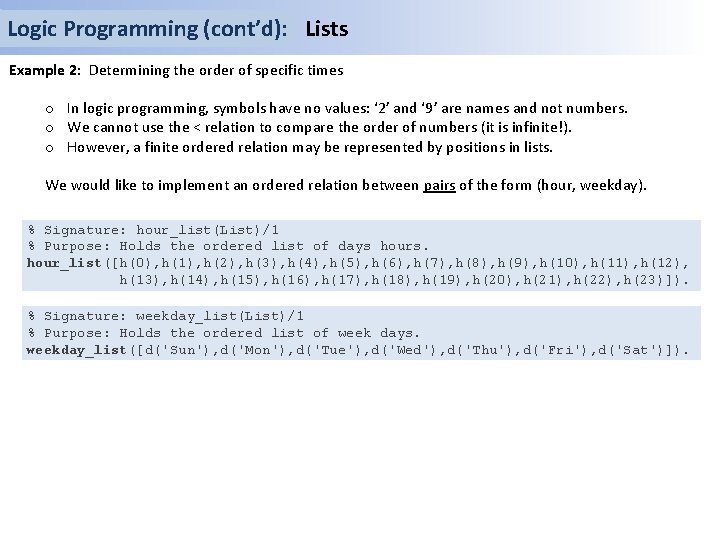
Logic Programming (cont’d): Lists Example 4: Merging sorted lists % Signature: lt(Obj 1, Obj 2)/2 % Purpose: Obj 1 precedes Obj 2 by some comparison criteria. lt(Time 1, Time 2) : - time_LT(Time 1, Time 2). % Signature: merge(Xs, Ys, Zs)/3 % Purpose: Zs is the sorted merge of the sorted lists Xs and Ys. Assumes % a predicate "lt" of order between elements of Xs and Ys. merge([X|Xs], [Y|Ys], [X|Zs]) : - lt(X, Y), merge(Xs, [Y|Ys], Zs). %1 merge([X|Xs], [X|Ys], [X, X|Zs]) : - merge(Xs, Ys, Zs). %2 merge([X|Xs], [Y|Ys], [Y|Zs]) : - lt(Y, X), merge([X|Xs], Ys, Zs). %3 merge(Xs, [], Xs). %4 merge([], Ys). %5 ? - merge([time(h(5), d('Sun')), time(h(5), d('Mon'))], X, [time(h(2), d('Sun')), time(h(5), d('Mon'))]). X = [time(h(2), d( 'Sun'))]

Logic Programming (cont’d): Lists Example 5: Merging sorted lists merge([X|Xs], [Y|Ys], [X|Zs]) : - lt(X, Y), merge(Xs, [Y|Ys], Zs). merge([X|Xs], [X|Ys], [X, X|Zs]) : - merge(Xs, Ys, Zs). merge([X|Xs], [Y|Ys], [Y|Zs]) : - lt(Y, X), merge([X|Xs], Ys, Zs). merge(Xs, [], Xs). merge([], Ys). ? -merge( [ time(h(1), d('Sun')), time(h(3), d('Wed')), time(h(5), d('Sat'))], [ time(h(2), d('Sun')), time(h(3), d('Wed'))], Xs) merge([t 1, t 3, t 5], [t 2, t 3], Xs) {X_1=t 1, Xs_1=[t 3, t 5], Y_1=t 2, Ys_1=[t 3], Xs=[t 1|Zs_1]} 1 lt(t 1, t 2), merge([t 3, t 5], [t 2, t 3], Zs_1) 2 – failure branch… 3 – failure branch… * merge([t 3, t 5], [t 2, t 3], Zs_1) 1 – failure branch… 2 – failure branch… {X_2=t 3, Xs_2=[t 5], Y_2=t 2, Ys_2=[t 3], Zs_1=[t 2|Zs_2]} 3 lt(t 2, t 3), merge([t 3, t 5], [t 3], Zs_2) * merge([t 3, t 5], [t 3], Zs_2) 1 – failure branch… {X_3=t 3, Xs_3=[t 5], Ys_3=[], Zs_2=[t 3, t 3|Zs_3]} 2 {Xs_4=[t 5], Zs_3=[t 5]} 4 merge([t 5], [], Zs_3) true 1 – failure branch…

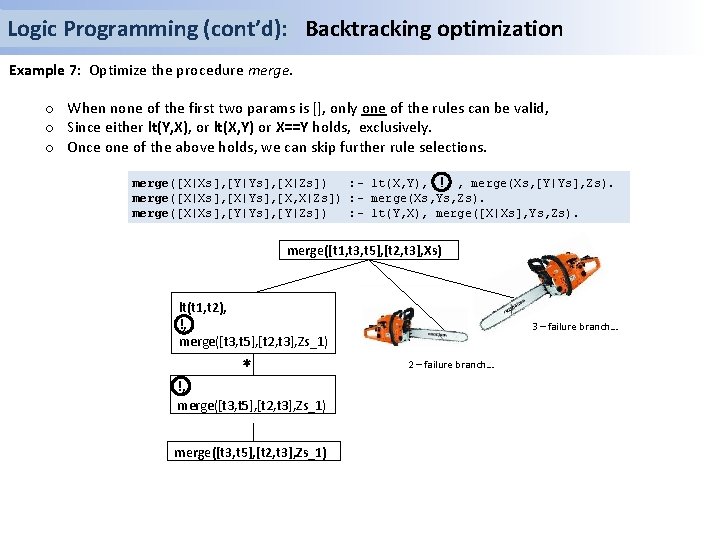
Logic Programming (cont’d): Backtracking optimization Example 7: Optimize the procedure merge. o When none of the first two params is [], only one of the rules can be valid, o Since either lt(Y, X), or lt(X, Y) or X==Y holds, exclusively. o Once one of the above holds, we can skip further rule selections. merge([X|Xs], [Y|Ys], [X|Zs]) : - lt(X, Y), ! , merge(Xs, [Y|Ys], Zs). merge([X|Xs], [X|Ys], [X, X|Zs]) : - merge(Xs, Ys, Zs). merge([X|Xs], [Y|Ys], [Y|Zs]) : - lt(Y, X), merge([X|Xs], Ys, Zs). merge([t 1, t 3, t 5], [t 2, t 3], Xs) lt(t 1, t 2), !, merge([t 3, t 5], [t 2, t 3], Zs_1) 3 – failure branch… * 2 – failure branch… !, merge([t 3, t 5], [t 2, t 3], Zs_1)

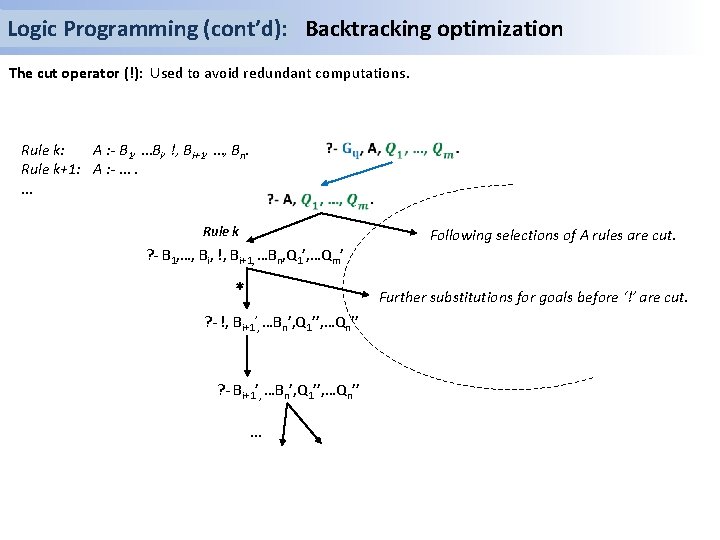
Logic Programming (cont’d): Backtracking optimization The cut operator (!): Used to avoid redundant computations. Rule k: A : - B 1, …Bi, !, Bi+1, …, Bn. Rule k+1: A : - …. … Rule k Following selections of A rules are cut. ? - B 1, …, Bi, !, Bi+1, …Bn, Q 1’, …Qm’ * Further substitutions for goals before ‘!’ are cut. ? - !, Bi+1’, …Bn’, Q 1’’, …Qn’’ ? - Bi+1’, …Bn’, Q 1’’, …Qn’’ …

Logic Programming (cont’d): Backtracking optimization Example 8: red VS green cuts. o Green cut: Helps optimizing the program by avoiding redundant computations. o Red cut: Omits possible solutions. o Red cuts are undesired, unless specifically required (E. g. , to provide only the first solution). Q: How many possible solutions does the following query have? ? - merge([], X). X = []; X = [] The query matches both facts 4 and 5: merge(Xs, [], Xs). merge([], Ys). To avoid this, we add ‘!’ to fact 4, rewriting it as a rule: merge(Xs, [], Xs): - !. merge([], Ys). A red cut! The number of solutions has changed!

Logic Programming (cont’d): Meta circular interpreter Recall the “waiting list” version of the meta-circular interpreter (seen in class): o Based on goals reduction, with explicit control of selection order (using a stack of goals). o Operates in two phases: 1. Preprocessing: The given program, P, is translated into a new program P’, which has a single predicate, rule, and consists of facts only. 2. Queries are applied to the new program using the procedure solve.

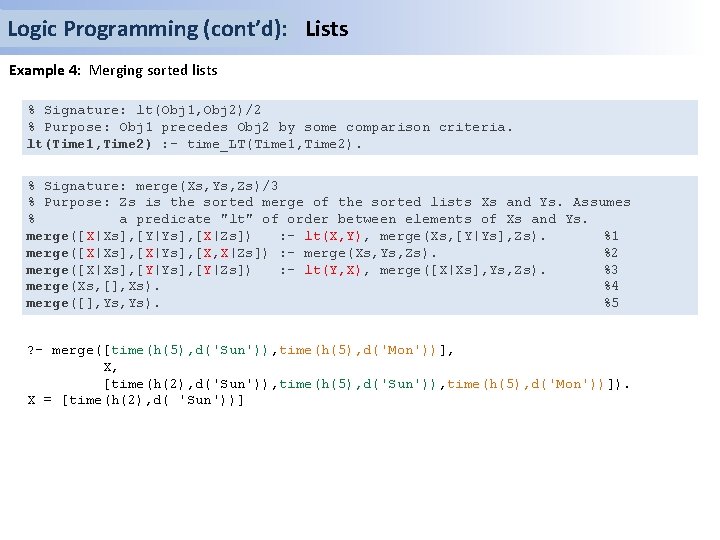
Logic Programming (cont’d): Meta circular interpreter Example 10: Applying the meta circular interpreter. member(X, [X|Xs]). member(X, [Y|Ys]) : - member(X, Ys ). % Signature: rule(Head, Body. List)/2 rule(member(X, [X|Xs]), true). rule(member(X, [Y|Ys]), [member(X, Ys)]). Preprocessing % Signature: solve(Exp)/1 % Purpose: Interpret with explicit management of a waiting list of goals. solve(Goal) : - solve(Goal, []). % Signature: solve(Goal, Rest_of_goals)/2 solve(true, Goals) : - solve([], Goals). solve([], []). % Nothing to prove, empty stack, done. solve([], [G | Goals]) : - solve(G, Goals). % Nothing to prove, non-empty stack, pop. % A list of goals: prove the first and push the rest. solve([A|B], Goals) : - extend_waiting_list([A|B], Goals, New. Goals), solve([], New. Goals). solve(A, Goals) : - rule(A, B), solve(B, Goals ).

solve(member(X, [a, b, c])) {Goal_1 = member(X, [a, b, c])} 1 solve(member(X, [a, b, c]), []) {A_2 = member(X, [a, b, c]), Goals_2 = []} rule(member(X, [a, b, c], B_2), solve(B_2, []) 5 {X_3 = X, Y_3 = a, Ys_3 = [b, c], B_2 = [member(X, [b, c])]} {X = a, X_3 = a, Xs_3 = [b, c], B_2 = []} 2 1 solve([], []) 2 true solve([member(X, [b, c])], []) ext-wait-list([member(X, [b, c])], [], New. Goals_4), solve([], New. Goals_4) * {X = a} rule(member(X, [X|Xs]), true). rule(member(X, [Y|Ys]), [member(X, Ys)]). solve(Goal) : - solve(Goal, []). solve(true, Goals) : - solve([], Goals). solve([], []). solve([], [G | Goals]) : - solve(G, Goals). solve([A|B], Goals) : - extend_waiting_list([A|B], Goals, New. Goals), solve([], New. Goals). {A_4 = member(X, [b, c]), B_4=[] Goals_4 = []} 4 {New. Goals_4 = [member(X, [b, c])]} solve([], [member(X, [b, c])] ) {G_5 = member(X, [b, c]), Goals_5 = []} 3 solve(member(X, [b, c]), []) {A_6 = member(X, [b, c]), Goals_6 = []} 5 rule(member(X, [b, c]), B_6), solve(B_6, []) {X = b, X_7 = b, Xs_7 = [c], B_6 = []} solve(true, []) {Goals_8 = []} solve(A, Goals) : - rule(A, B), solve(B, Goals ). solve([], []) 2 {X = b} true 1 … 1