Logic of Informatics Converse Inverse Contrapositive Equivalence Tautology

Logic of Informatics Converse, Inverse, Contrapositive, Equivalence, Tautology and Contradiction

Last Lecture • Propositions • Statement • Truth table

Propositions • A proposition is any meaningful statement that is either true or false, but not both. • We will use lowercase letters, such as p, q, r, … , to represent propositions

Statement • The truth value of a proposition is true, denoted by T, if it is a true statement and false, denoted by F, if it is a false statement. • Statements that are not propositions include questions and commands

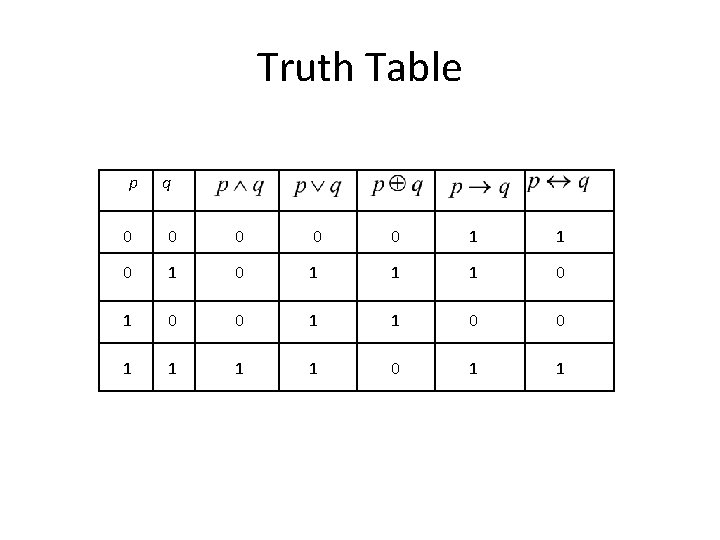
Truth Table p q 0 0 0 1 0 1 1 0 1 0 1 0 1 1 0 1

Reminder! • Conditional: p q. • The phrase after the word “if” is the hypothesis. (p) • The phrase after the word “then” is the conclusion. (q)

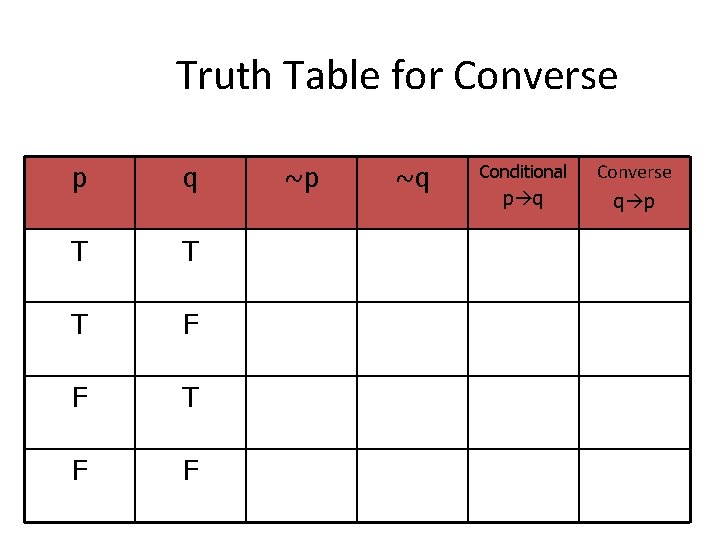
Converse • Converse – switching the places of the hypothesis and conclusion. • Ex. Conditional: If two angles have the same measure, then they are congruent. • Converse : If they are congruent, then two angles have the same measure.

Conditional to Converse • Conditional: p q • Converse : q p • Conditional: ~p q • Converse : q ~p • Conditional: ~q ~p • Converse : ~p ~q

Truth Table for Converse p q T T T F F ~p ~q Conditional p q Converse q p

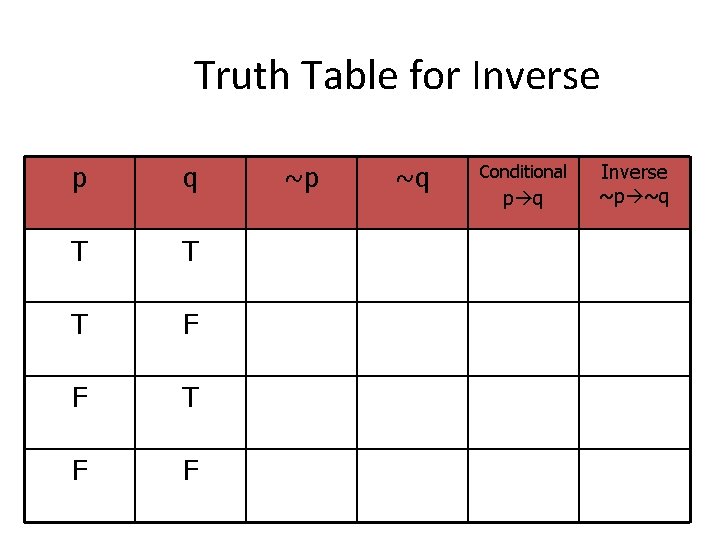
Inverse • Inverse – Negating both the hypothesis and conclusion of the conditional. • Ex. Conditional: If two angles have the same measure, then they are congruent. • Inverse: If two angles do not have the same measure, then they are not congruent.

Conditional to Inverse • Conditional: p q • Inverse: ~p ~q • Conditional: ~p q • Inverse : p ~q • Conditional: ~q ~p • Inverse : q p

Truth Table for Inverse p q T T T F F ~p ~q Conditional p q Inverse ~p ~q

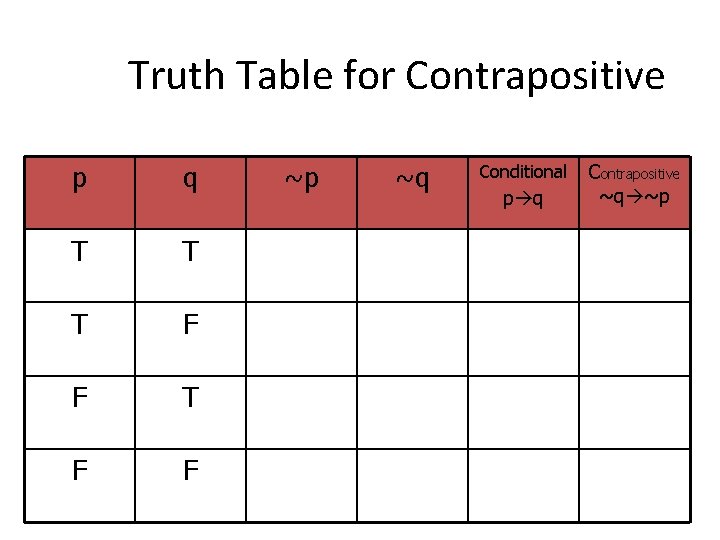
Contrapositive • Contrapositive – Negating AND exchanging both the hypothesis and conclusion • Ex. Conditional: If two angles have the same measure, then they are congruent. • Contrapositive: If two angles are not congruent then they do not have the same measure.

Conditional to Contrapositive • Conditional: p q • Contrapositive: ~q ~p • Conditional: ~p q • Contrapositive: ~q p • Conditional: ~q ~p • Contrapositive: p q

Truth Table for Contrapositive p q T T T F F ~p ~q Conditional p q Contrapositive ~q ~p

Practice • Write the converse, inverse, and contrapositive of the following conditional statement: If two angles equal 90°, then they are complementary.

Answer • Converse: If two angles are complementary, then they equal 90° • Inverse: If two angle do not equal 90° then they are not complementary • Contrapositive: If two angles are not complementary then they do not equal 90°

Tautology •

Contradiction •

Equivalence • Two compound statements A and B are logically equivalent if thet have The same truth, denoted by A B. The Truth Table of Equivalence p q ~p p→q ~p v q T T F T T T F F F T T T

Exercise 1 Let p states ‘Today is cloudy’ and q states ‘Today is raining’. Write a sentence that stated the following symbols: a) - p f) – q -> - p b) p v q g) - p <=> -q c) - p v q h) p <=> - q d) - (p v q) i) (p <=> -q) v p e) p ^ q j) - p -> -q

Exercise 2 Let p states ‘Duta is handsome’ and q states ‘Diana is beautiful’. Write the following sentences into symbols using p and q. a. b. c. d. e. Duta is handsome and Diana is beautiful. Duta is not handsome if Diana is not beautiful. Diana is beautiful or Duta is not handsome. Diana is not beautiful if and only if Duta is not handsome. It is not true that Diana is not beautiful and Duta is not handsome.

Exercise 3 Determine the truth value of: a. If 3 + 2 = 23, then 42 = 42. b. New York is in Italia if and only if 3 is odd numbers. c. It is not true that 10 – 5 = 15 and 25 – 5 = 20. d. Samarinda is in Sulawesi or the capital of east Kalimantan is not Samarinda. e. The results of 52 divide by 13 is 4 and it is not true that 2 + 4 = 6

Exercise 4 Determine the truth value of the following compound statement p: Today the sun is shining bright (T) q: Today the wind is blowing hard (F) a. If today the sun is shining brightly then the wind is blowing hard. b. If today the sun is shining brightly then the wind is not blowing hard c. If today the sun is not shining brightly then the wind is blowing hard. d. If today the sun is not shining brightly then the wind is not blowing hard.

Exercise 5 Determine the truth value of a compound statement which is based on the following statement: p: 2 is prime number (T) q: 2 + 6 = 12 (F) a. b. c. d. 2 is prime number if and only if 2 + 6 = 12 2 is prime number if and only if 2 + 6 is not equal 12 2 is not prime number if and only if 2 + 6 = 12 2 is not prime number if and only if 2 + 6 is not equal 12

Exercise 6 • Write the converse, inverse and contrapositive of the statement exercise 4.

Exercise 7 •