logic model s analysis daniel jackson static analysis

logic, model s& analysis daniel jackson static analysis symposium ·santa barbara · june 2 k

my green eggs and ham ·two languages in any analysis ·first order relational logic ·models in their own right 2 2

plan of talk ·Alloy, a RISC notation ·models of software ·analysis reduced to SAT ·finding bugs with constraints 3 3

an example model Ceilings. And. Floors { domain { Man, Platform } state { ceiling, floor : Man -> Platform! } // one man’s ceiling is another man’s floor inv { all m: Man | some n: Man - m | m. ceiling = n. floor } // one man’s floor is another man’s ceiling assert { all m: Man | some n: Man - m | m. floor = n. ceiling } } 4 4

kernel: type decls d decls, x typexps, t types scalars are singleton sets d : : = v : x x : : = t | t -> t | t => x sample decls File, Dir, Root : Object dir : Object => Name -> Object entries : Object -> Dir. Entry name : Dir. Entry -> Name contents : Dir. Entry -> Object parent : Object -> Object 5 funcs are first-order (t 1 => t 2 -> t 3) equiv to (t 1 x t 2 -> t 3) missing: (t 1 -> t 2) -> t 3 5

kernel: expressions f formulas, e exps, v vars e : : = e + e | e & e | e - e |~e|+e ops image | e [v] application | {v : t | f} comprehension |v sample exprs Root. ~parent & File d. entries. contents set ops navigatio n relational |e. e 6 6

kernel: formulas f : : = e in e | f && f | !f | all v : t | f subset logic ops quantification in used for subset and membership sample formulas File+Dir-Root in Root. +~parent all d: Dir. Entry | ! d in d. contents. entries 7 7

shorthands declarations ·domain {d} declares d : _d ·use sets on RHS ·multiplicities: + 1, ? 1, ! 1 domain {Object, Dir. Entry, Name} state { partition File, Dir : Object Root: Dir ! entries: Dir ! -> Dir. Entry name: Dir. Entry -> Name ! contents: Dir. Entry -> Object ! parent (~children) : Object -> Dir ? } 8 8

more shorthands quantifiers sole v: t | f all x | f domain Qe some w: t | { v: t | f } in w all x : d | f where d is inferred Q v | v in e sample invariants // object has at most one parent all o | sole o. parent // root has no parents no Root. parent // all other directories have one parent all d: Dir - Root | one d. parent 9 9

sample model: intentional naming INS ·Balakrishnan et al, SOSP 1999 ·naming scheme based on specs why we picked INS ·naming vital to infrastructure ·INS more flexible than Jini, COM, etc what we did ·analyzed lookup operation ·based model on SOSP paper & Java code 10 10

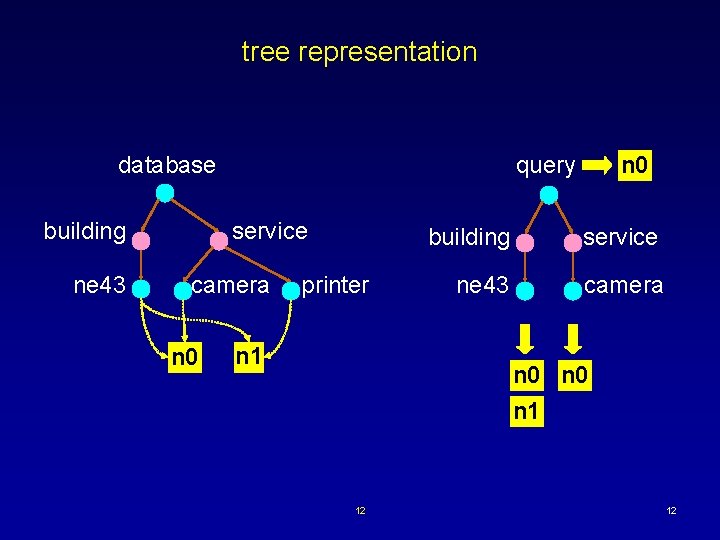
intentional naming attribute/value pairs city: cambridge hierarchical specs city: cambridge, building: ne 43, room: 524 service: camera, resolution: hi service: printer, postscript: level 2 lookup ·database maps spec to set of records ·query is set of specs ·lookup returns records meeting all specs 11 11

tree representation database building ne 43 service camera n 0 query printer n 1 building service ne 43 camera n 0 n 1 12 12

strategy model database & queries ·characterize by constraints ·generate samples check properties ·obvious no record returned when no attributes match ·claims “wildcards are equivalent to omissions” ·essential additions to DB don’t reduce query results discuss and refine … 13 13

alloy model: state model INS { domain {Attribute, Value, Record} state { Root : fixed Value! val. Q : Attribute? -> Value? att. Q : Value? -> Attribute val. DB : Attribute? -> Value att. DB : Value? -> Attribute rec : Value + -> Record lookup : Value -> Record } 14 14

alloy model: constraints // Root is not the value of an attribute inv Q 1 {no Root. ~val. Q} // if query and DB share a leaf value, lookup returns its records inv Lookup 1 {all v | no v. att. Q || no v. att. DB -> v. lookup = v. rec} // adding a record doesn’t reduce results assert Lookup. OK 7 {Add. Record -> Root. lookup in Root. lookup'} 15 15

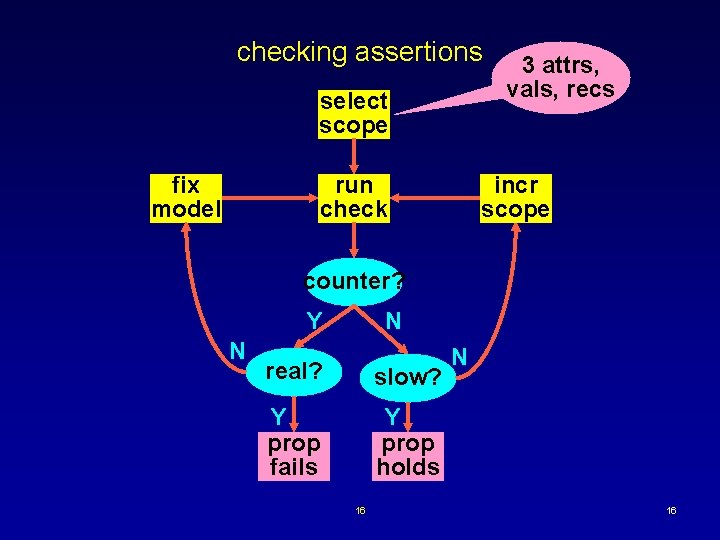
checking assertions select scope fix model run check 3 attrs, vals, recs incr scope counter? Y N N real? slow? Y prop fails Y prop holds 16 N 16

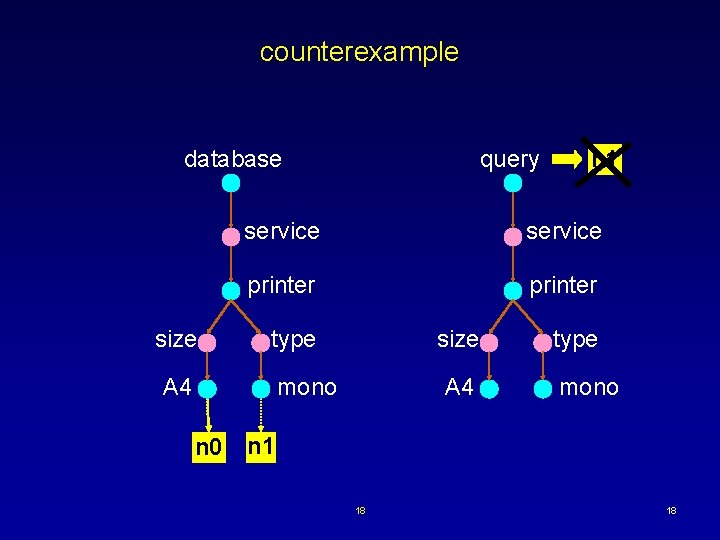
results 12 assertions checked ·when query is subtree, ok ·found known bugs in paper ·found bugs in fixes too ·monotonicity violated 17 17

counterexample database size query service printer type A 4 size mono n 0 n 1 A 4 type mono n 1 18 18

time & effort costs 2 weeks modelling, ~70 + 50 lines Alloy cf. 1400 + 900 lines code all bugs found in < 10 secs with scope of 4 2 records, 2 attrs, 3 values usually enough cf. a year of use exhausts scope of 5 in 30 secs max space of approx 10^20 cases 19 19

other modelling experiences microsoft COM (Sullivan) ·automated & simplified: 99 lines ·no encapsulation air traffic control (Zhang) ·collaborative arrival planner ·ghost planes at US/Canada border PANS phone (Zave) ·multiplexing + conferencing ·light gets stuck 20 20

why modelling improves designs rapid experimentation articulating essence simplifying design catching showstopper bugs 21 21

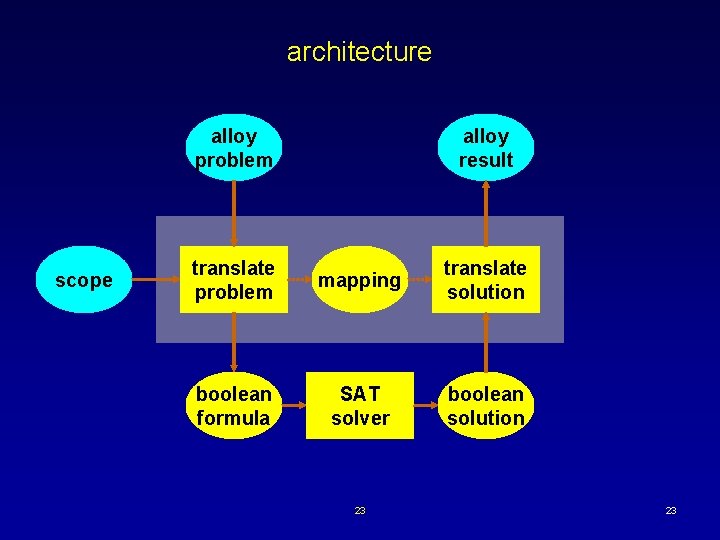
how analyzer works what you learned in CS 101 · 3 -SAT: first NP-c problem ·to show a problem is hard reduce SAT to it small scope hypothesis most interesting cases have illustrations in small scopes what we know ·SAT is usually easy ·to show a problem is easy reduce it to SAT key to reduction ·consider finite scope: type 22 22

architecture alloy problem scope alloy result translate problem mapping translate solution boolean formula SAT solver boolean solution 23 23

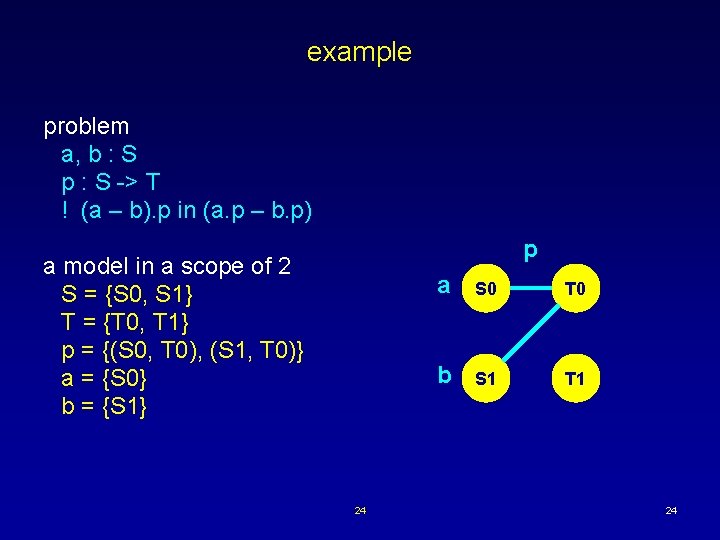
example problem a, b : S p : S -> T ! (a – b). p in (a. p – b. p) p a model in a scope of 2 S = {S 0, S 1} T = {T 0, T 1} p = {(S 0, T 0), (S 1, T 0)} a = {S 0} b = {S 1} 24 a S 0 T 0 b S 1 T 1 24

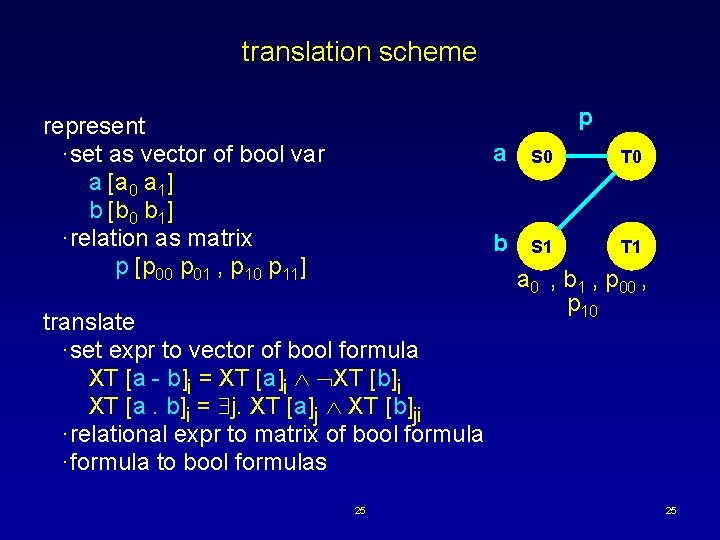
translation scheme p represent ·set as vector of bool var a [a 0 a 1] b [b 0 b 1] ·relation as matrix p [p 00 p 01 , p 10 p 11] translate ·set expr to vector of bool formula XT [a - b]i = XT [a]i XT [b]i XT [a. b]i = j. XT [a]j XT [b]ji ·relational expr to matrix of bool formula ·formula to bool formulas 25 a S 0 T 0 b S 1 T 1 a 0 , b 1 , p 00 , p 10 25

translation a b p a–b (a – b). p a. p b. p a. p – b. p [a 0 a 1] [b 0 b 1] [p 00 p 01 , p 10 p 11] [a 0 b 0 a 1 b 1] [(a 0 b 0 p 00) (a 1 b 1 p 10) …] [(a 0 p 00) (a 1 p 10) (a 0 p 01) (a 1 p 11)] [(b 0 p 00) (b 1 p 10) (b 0 p 01) (b 1 p 11)] [((a 0 p 00) (a 1 p 10)) ((b 0 p 00) (b 1 p 10)) …] ! (a – b). p in (a. p – b. p) (((a 0 b 0 p 00) (a 1 b 1 p 10) ((a 0 p 00) (a 1 p 10)) ((b 0 p 00) (b 1 p 10)))) … 26 26

tricks quantifiers ·could expand into conjunctions ·but how to make modular? ·translate formula into tree indexed on var avoiding blowup ·solvers expect CNF ·standard var intro tricks symmetry ·all our domains are uninterpreted ·many equivalent assignments ·add symmetry-breaking predicates 27 27

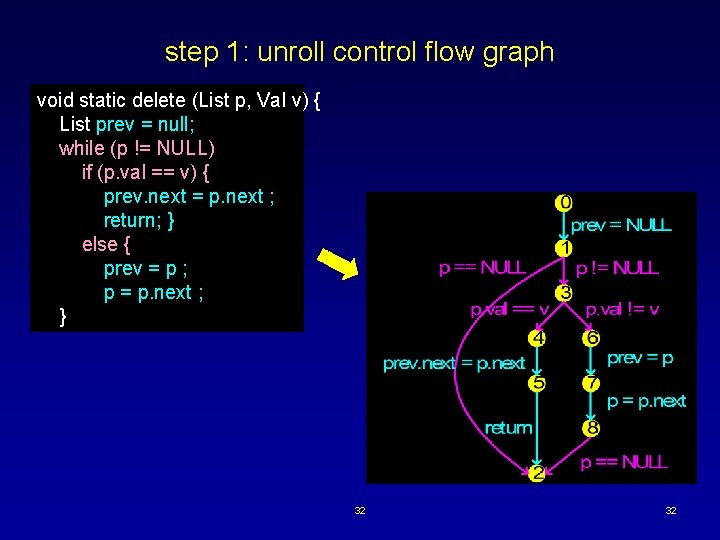
how (not) to delete class List {List next; Val val; } void static delete (List p, Val v) { List prev = null; while (p != NULL) if (p. val == v) { prev. next = p. next ; return; } else { prev = p ; p = p. next ; } 28 28

specifying delete basic spec p. *next’ = p. *next – {c | c. val = v} as Alloy model domain {List, Val} state { next : List -> List? val : List -> Val? p : List? , v : Val? } op Merge. Code { … } op Merge. Spec {p. *next’ = p. *next – {c | c. val = v}} assert {Merge. Code -> Merge. Spec} 29 29

hacking delete (1) counter #1: first cell has value v cond Mask {p. val != v} assert {Merge. Code && Mask -> Merge. Spec} p val v 30 30

hacking delete (2) counter #2: two cells with value v cond RI {all x | sole c: p. *next | c. val = x} assert {Merge. Code && Mask && RI -> Merge. Spec} assert {Merge. Code && RI -> RI’} p val next val 31 v val 31

step 1: unroll control flow graph void static delete (List p, Val v) { List prev = null; while (p != NULL) if (p. val == v) { prev. next = p. next ; return; } else { prev = p ; p = p. next ; } 32 32

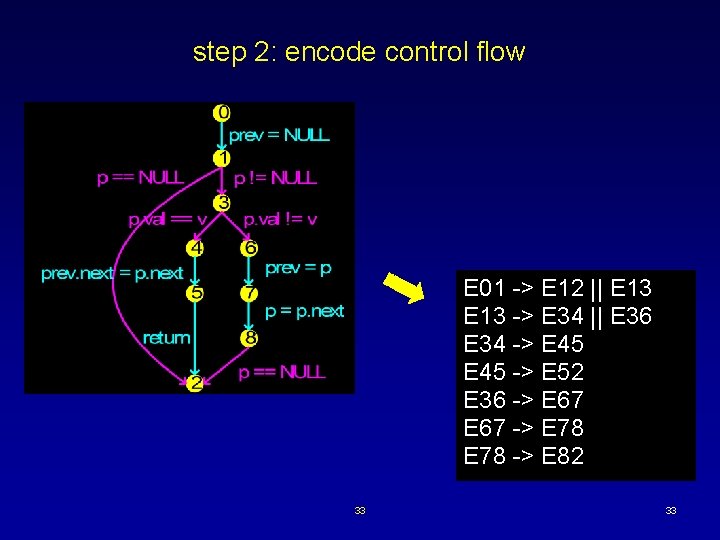
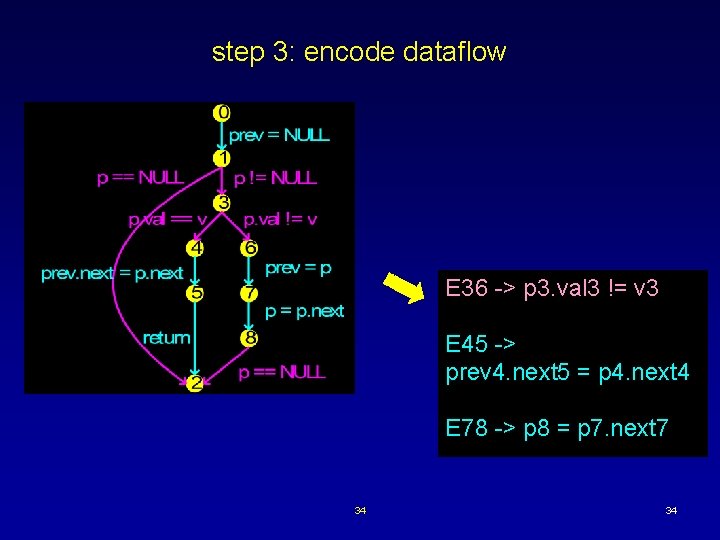
step 2: encode control flow E 01 -> E 12 || E 13 -> E 34 || E 36 E 34 -> E 45 -> E 52 E 36 -> E 67 -> E 78 -> E 82 33 33

step 3: encode dataflow E 36 -> p 3. val 3 != v 3 E 45 -> prev 4. next 5 = p 4. next 4 E 78 -> p 8 = p 7. next 7 34 34

frame conditions must say what doesn’t change ·so add p 6 = p 7 but ·don’t need a different p at each node ·share vars across paths ·eliminates most frame conditions 35 35

sample results on Sagiv & Dor’s suite of small list procedures ·reverse, rotate, delete, insert, merge ·wrote partial specs (eg, set containment on cells) ·predefined specs for null deref, cyclic list creation anomalies found · 1 unrolling ·scope of 1 ·< 1 second specs checked · 3 unrollings ·scope of 3 ·< 12 seconds 36 36

promising? nice features ·expressive specs ·counterexample traces ·easily instrumented compositionality ·specs for missing code ·summarize code with formula analysis properties ·code formula same for all specs ·exploit advances in SAT 37 37

summary ·Alloy, a tiny logic of sets & relations ·declarative models, not abstract programs ·analysis based on SAT ·translating code to Alloy challenge ·checking key design properties ·global object model invariants ·looking at CTAS air-traffic control ·abstraction, shape analysis …? 38 38

related work checking against logic ·Sagiv, Reps & Wilhelm’s PSA ·Extended Static Checker using constraints ·Ernst, Kautz, Selman & co: planning ·Biere et al: linear temporal logic ·Podelski’s array bounds extracting models from code ·SLAM’s boolean programs ·Bandera’s automata 39 39

You do not like them. So you say. Try them! And you may. Try them and you may, I say. sdg. lcs. mit. edu/alloy 40 40