Logic Math Studies IB Propositions truth tables logic

Logic Math Studies IB Propositions, truth tables, logic symbols, negation, conjunction, disjunction.

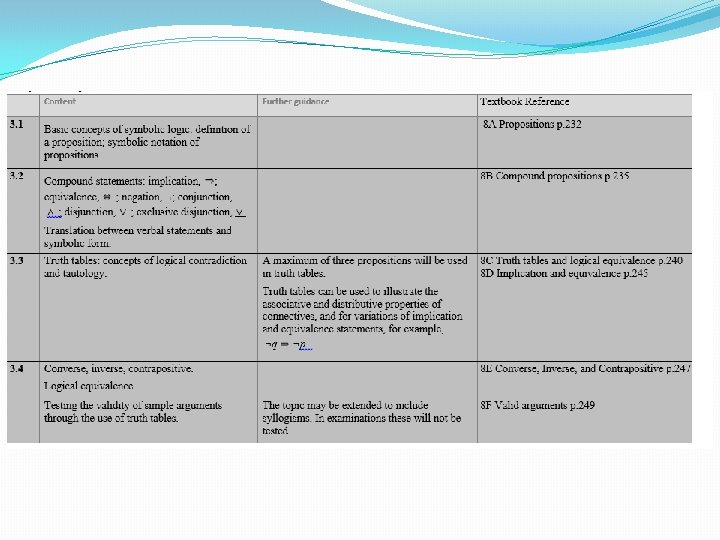
Formula Booklet page 4

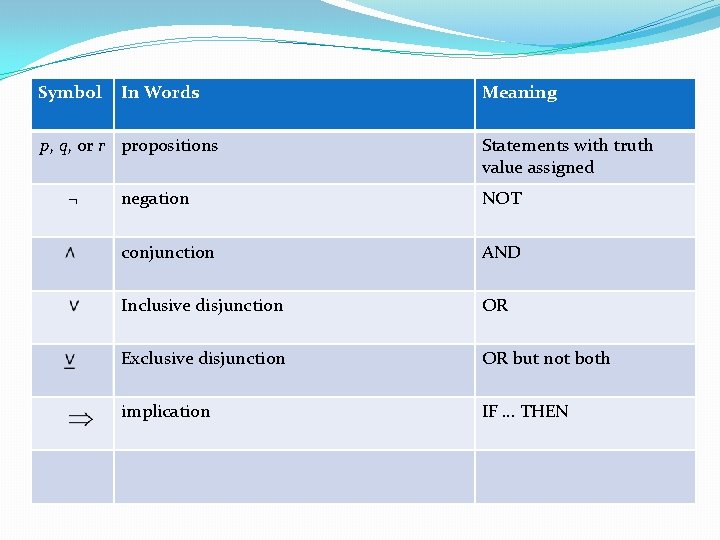
Symbol In Words p, q, or r propositions ¬ Meaning Statements with truth value assigned negation NOT conjunction AND Inclusive disjunction OR Exclusive disjunction OR but not both implication IF … THEN

What is Logic? Logic is a way to describe situations or knowledge that enables us to reason from existing knowledge to new conclusions. For example: All college students are poor I am a college student Therefore, I am poor If the original statement is false, the conclusion is still logical (it just may be false) All college students are rich (not true) I am a college student Therefore, I am rich!

Logical Reasoning You have four cards. A letter A – Z is the blue side. A number 0 – 9 is on the green side. You have these cards: 5 E K 4 7 What card do you turn over to test the rule “If a card has a vowel on the blue side, it must have an even number on the greenside?

Propositions.

Sets and Logical Reasoning A proposition is a statement that may be true or false. For Example, “Mrs Graham is a maths teacher” is a true proposition “Mrs Graham is 2 meters tall” is a false proposition “Today is Saturday” is indeterminate because it may be true of false depending on the circumstances. All of these are examples of simple propositions.

Propositions Consider the following statements: Go get the book Have you seen my new shirt? The dog is behind the shed Which statement is a proposition? The dog is behind the shed. Rewrite the others so they are propositions Sophia got the book. Jackson saw my new shirt.

Representing propositions We represent propositions by letters such as p, q, and r. For Example: p: Mrs Graham is a math teacher q: Mrs Graham is 2 m tall r: Today is Sunday Opposites are represented by negation (¬) ¬p represents the opposite of p We read that as “not p” ¬p: Mrs Graham is not a math teacher ¬q: Mrs Graham is not 2 m tall ¬r: Today is not Sunday

A proposition is a statement that is either true (T) or false (F); it cannot be both true and false at the same time. Which of the following are propositions? A. B. C. D. E. F. G. H. I. Riley studies IB mathematics. 5 < 6 Have a nice day! Is it snowing? The sun is not shining. The moon is made of green cheese. A week consists of five days. The glass is full. The air-con is on.

Write the negation of the statement ‘n is a prime number’ p: n is a prime number ¬ p: n is not a prime number Write the negation of ‘this word starts with a vowel’ without using the word ‘not’. ‘this word starts with a consonant’

Truth Values Because a proposition is a statement that can be either true or false, its Truth Values are T for true and F for false. This may be represented in a table. p : Carla has black hair T F ¬ p : Carla does not have black hair

Truth table for negation

Exercise 8 A. 1 p 233 Questions 1 -5 Exercise 8 A. 2 Questions 1 -4

Compound Propositions

Compound propositions. A compound proposition is made up of simple propositions joined together by connectives, The five connectives that we will use most commonly are: NOT AND OR OR IF … THEN

Conjunctions For the following propositions: p: Ty is a superhero q: Sofia is a basketball star What is p^q : Ty is a superhero and Sofia is a basketball star What is ¬p^q Ty is not a superhero and Sofia is a basketball star

Conjunction: Truth Value The truth value of a conjunction is only true with BOTH the propositions are true. p T T F q T F F

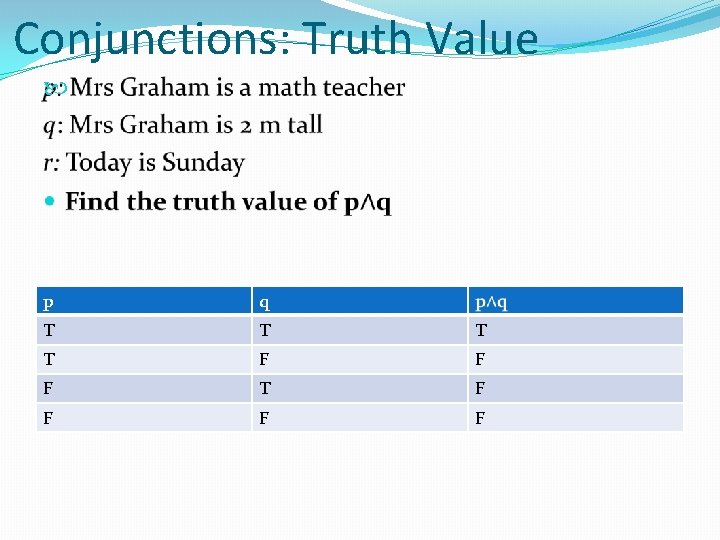
Conjunctions: Truth Value p q T T F F F T F F

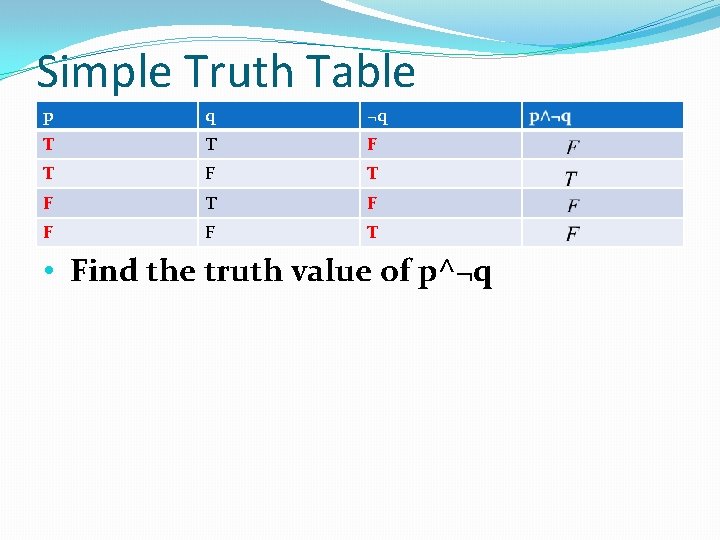
Simple Truth Table p q ¬q T T F T F F F T • Find the truth value of p^¬q

Complete the truth table for T F F F T F is a logical contradiction because all the entries in the third column are false.

Disjunctions p q T T F F F

Disjunction p q p∨q T T F F F

Exclusive Disjunction p q T T F T F T T F F F

Venn Diagrams You will go to Hawaii by boat or by plane p: you will go by boat q: you will go by plane boat plane

Practice p: London is the capital of England q: 45 – 5 = 4 r: Cows have 4 legs Find the truth value of the following: p ^ q q v r ¬q ^ r ¬(p v q) p v r