Logic Learning Objectives q Learn about statements propositions

Logic: Learning Objectives q Learn about statements (propositions) q Learn how to use logical connectives to combine statements q Explore how to draw conclusions using various argument forms q Become familiar with quantifiers and predicates q CS q Boolean data type q If statement q Impact of negations q Implementation of quantifiers Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Definition: Methods of reasoning, provides rules and techniques to determine whether an argument is valid q Theorem: a statement that can be shown to be true (under certain conditions) q. Example: If x is an even integer, then x + 1 is an odd integer q. This statement is true under the condition that x is an integer is true Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q A statement, or a proposition, is a declarative sentence that is either true or false, but not both q Lowercase letters denote propositions q. Examples: qp: 2 is an even number (true) qq: 3 is an odd number (true) qr: A is a consonant (false) q. The following are not propositions: qp: My cat is beautiful qq: Are you in charge? Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Truth value q One of the values “truth” or “falsity” assigned to a statement q True is abbreviated to T or 1 q False is abbreviated to F or 0 q Negation q The negation of p, written ∼p, is the statement obtained by negating statement p q. Truth values of p and ∼p are opposite q. Symbol ~ is called “not” ~p is read as as “not p” q. Example: qp: A is a consonant q~p: it is the case that A is not a consonant qq: Are you in charge? Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Truth Table q Conjunction q Let p and q be statements. The conjunction of p and q, written p ^ q , is the statement formed by joining statements p and q using the word “and” q. The statement p∧q is true if both p and q are true; otherwise p∧q is false Discrete Mathematical Structures: Theory and Applications 5

Mathematical Logic q Conjunction q. Truth Table for Conjunction: Discrete Mathematical Structures: Theory and Applications 6

Mathematical Logic q Disjunction q. Let p and q be statements. The disjunction of p and q, written p v q , is the statement formed by joining statements p and q using the word “or” q. The statement p v q is true if at least one of the statements p and q is true; otherwise p v q is false q. The symbol v is read “or” Discrete Mathematical Structures: Theory and Applications 7

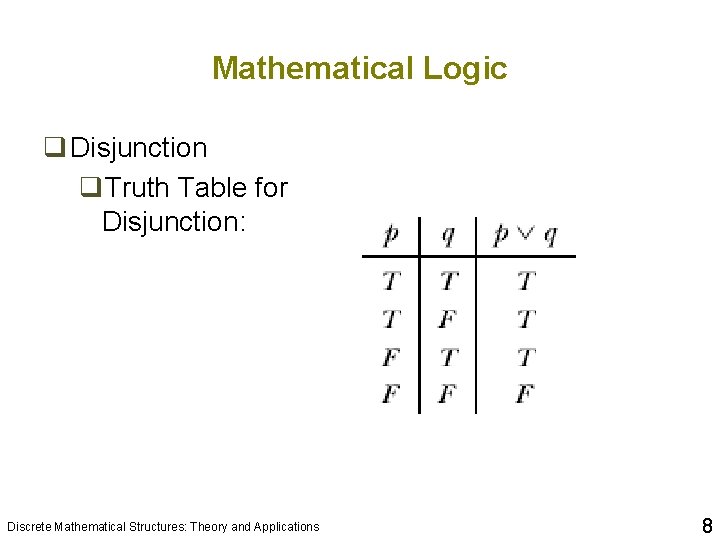
Mathematical Logic q Disjunction q. Truth Table for Disjunction: Discrete Mathematical Structures: Theory and Applications 8

Mathematical Logic q Implication q. Let p and q be statements. The statement “if p then q” is called an implication or condition. q. The implication “if p then q” is written p q qp q is read: q“If p, then q” q“p is sufficient for q” qq if p qq whenever p Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Implication q. Truth Table for Implication: qp is called the hypothesis, q is called the conclusion Discrete Mathematical Structures: Theory and Applications 10

Mathematical Logic q Implication q. Let p: Today is Sunday and q: I will wash the car. The conjunction p q is the statement: qp q : If today is Sunday, then I will wash the car q. The converse of this implication is written q p q. If I wash the car, then today is Sunday q. The inverse of this implication is ~p ~q q. If today is not Sunday, then I will not wash the car q. The contrapositive of this implication is ~q ~p q. If I do not wash the car, then today is not Sunday Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Biimplication q. Let p and q be statements. The statement “p if and only if q” is called the biimplication or biconditional of p and q q. The biconditional “p if and only if q” is written p q qp q is read: q“p if and only if q” q“p is necessary and sufficient for q” q“q if and only if p” q“q when and only when p” Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Biconditional q. Truth Table for the Biconditional: Discrete Mathematical Structures: Theory and Applications 13

Mathematical Logic q Statement Formulas q Definitions q Symbols p , q , r , . . . , called statement variables q Symbols ~, , v, →, and ↔ are called logical ^ connectives 1) A statement variable is a statement formula 2) If A and B are statement formulas, then the expressions (~A ), (A B) , (A v B ), (A → B ) ^ and (A ↔ B ) are statement formulas q Expressions are statement formulas that are constructed only by using 1) and 2) above Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Precedence of logical connectives is: q~ highest q ^ second highest q v third highest q→ fourth highest q↔ fifth highest Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Example: q. Let A be the statement formula (~(p v q )) → (q p ) ^ q. Truth Table for A is: Discrete Mathematical Structures: Theory and Applications 16

Mathematical Logic q Tautology q. A statement formula A is said to be a tautology if the truth value of A is T for any assignment of the truth values T and F to the statement variables occurring in A q Contradiction q. A statement formula A is said to be a contradiction if the truth value of A is F for any assignment of the truth values T and F to the statement variables occurring in A Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Logically Implies q. A statement formula A is said to logically imply a statement formula B if the statement formula A → B is a tautology. If A logically implies B, then symbolically we write A → B q Logically Equivalent q. A statement formula A is said to be logically equivalent to a statement formula B if the statement formula A ↔ B is a tautology. If A is logically equivalent to B , then symbolically we write A ≡ B Discrete Mathematical Structures: Theory and Applications

Mathematical Logic Discrete Mathematical Structures: Theory and Applications

Mathematical Logic q Proof of (~p ^ q ) → (~(q →p )) Discrete Mathematical Structures: Theory and Applications 20

Mathematical Logic q Proof of (~p ^q)→ Discrete Mathematical Structures: Theory and Applications (~(q →p )) [continued] 21

Validity of Arguments q Proof: an argument or a proof of a theorem consists of a finite sequence of statements ending in a conclusion q Argument: a finite sequence of statements. q The final statement, , is the conclusion, and the statements are the premises of the argument. q An argument is logically valid if the statement formula is a tautology. Discrete Mathematical Structures: Theory and Applications

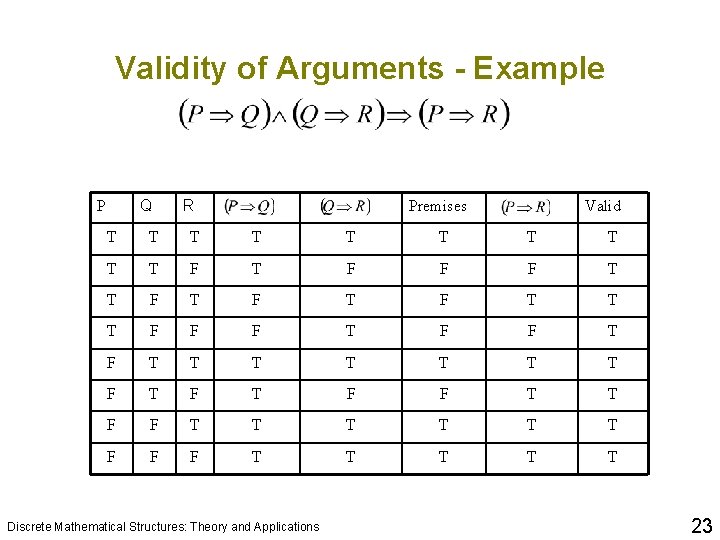
Validity of Arguments - Example Q P R Premises Valid T T T T T F T F F F T T F T F T T T F F F T F T T T T F T F F T T T T F F F T T T Discrete Mathematical Structures: Theory and Applications 23

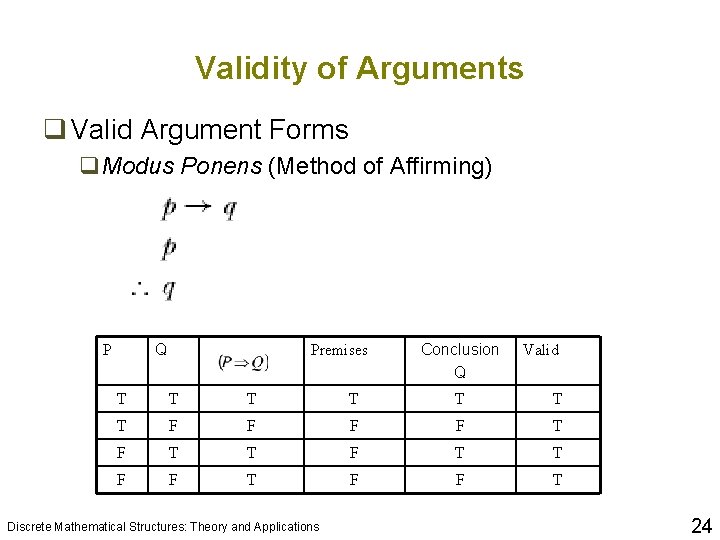
Validity of Arguments q Valid Argument Forms q. Modus Ponens (Method of Affirming) Q P Premises Conclusion Q Valid T T T T F F T F T T F F T Discrete Mathematical Structures: Theory and Applications 24

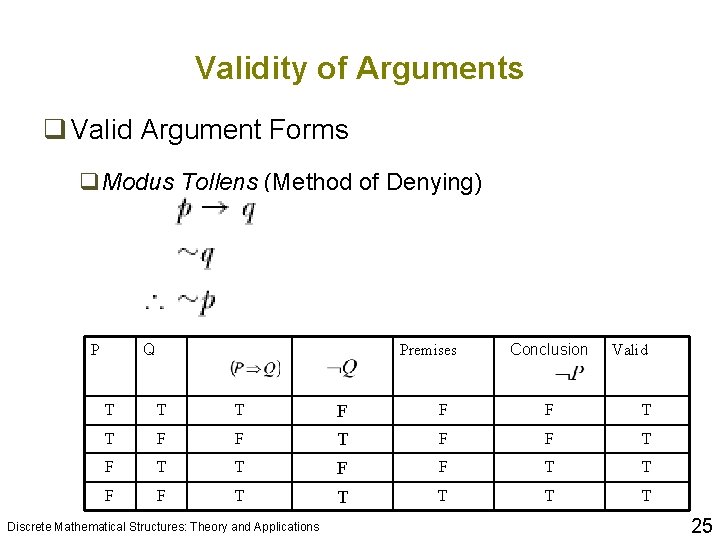
Validity of Arguments q Valid Argument Forms q. Modus Tollens (Method of Denying) Q P Premises Conclusion Valid T T T F F F T T F F T T T Discrete Mathematical Structures: Theory and Applications 25

Validity of Arguments q Valid Argument Forms q. Disjunctive Syllogisms Discrete Mathematical Structures: Theory and Applications 26

Validity of Arguments q Valid Argument Forms q Hypothetical Syllogism (proven earlier) q Dilemma Discrete Mathematical Structures: Theory and Applications 27

Validity of Arguments q Valid Argument Forms q. Conjunctive Simplification Discrete Mathematical Structures: Theory and Applications 28

Validity of Arguments q Valid Argument Forms q. Disjunctive Addition Discrete Mathematical Structures: Theory and Applications 29

Validity of Arguments q Valid Argument Forms q. Conjunctive Addition Discrete Mathematical Structures: Theory and Applications 30

Validity of Arguments – Formal Derivation q Prove q Formal Derivation Rule 1. P Q 2. Q R Premise 3. 4. 5. Assumption 1, 3, MP 2, 4, MP P Q R 6. P R DT Comment Assume P R is now proved Discharge P, ie, P is no longer to be used, and conclude that P R q Uses Deduction Theorem (DT) Discrete Mathematical Structures: Theory and Applications 31

Quantifiers and First Order Logic q Have dealt with Propositional Logic (Calculus) so far q Propositional variables, constants, expressions q Dealt with truth or falsity of expressions as a whole q Consider: 1. All cats have tails 2. Tom is a cat 3. Tom has a tail q Cannot conclude 3, given 1 and 2 using propositional logic q Predicate Calculus – allows us to identify individuals such as Tom together with properties and predicates. Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Predicate or Propositional Function q. Let x be a variable and D be a set; P(x) is a sentence q. Then P(x) is called a predicate or propositional function with respect to the set D if for each value of x in D, P(x) is a statement; i. e. , P(x) is true or false q. Moreover, D is called the domain of the discourse and x is called the free variable Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic Propositional function example #1 Let P(x) be the statement: x is an odd integer Let D be the set of all positive integers. Then P is a propositional function with domain of discourse D. • For each x in D , P(x) is a proposition, i. e. a sentence which is either true or false. • P(1): 1 is an odd integer – True • P(14): 14 is an odd integer - False Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic Propositional function example #2 Let P(x) be the statement: the baseball player hit over. 300 in 2003 Let D be the set of all baseball players. Then P is a propositional function with domain of discourse D. • For each x in D , P(x) is a proposition, i. e. a sentence which is either true or false. • P(Barry Bonds): Barry Bonds hit over. 300 in 2003 - True • P(Alex Rodriguez): Alex Rodriguez hit over. 300 in 2003 - False Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Predicate or Propositional Function q. Example: q Q(x, y) : x > y, where the Domain is the set of integers q Q is a 2 -place predicate q Q is T for Q(4, 3) and Q is F for Q (3, 4) Discrete Mathematical Structures: Theory and Applications 36

Quantifiers and First Order Logic q Universal Quantifier q. Let P(x) be a predicate and let D be the domain of the discourse. The universal quantification of P(x) is the statement: q. For all x, P(x) or q. For every x, P(x) q. The symbol is read as “for all and every” q q Two-place predicate: Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Universal Quantifier Examples q Consider the statement q It is true if P(x) is true for every x in D q It is false if P(x) is false for at least one x in D q Consider real numbers. with D being the set of all q The statement is true because for every real number x, it is true that the square of x is positive or zero. q Consider that with D being the set of real numbers is false. Why? Discrete Mathematical Structures: Theory and Applications 38

Quantifiers and First Order Logic q Existential Quantifier q. Let P(x) be a predicate and let D be the domain of the discourse. The existential quantification of P(x) is the statement: q. There exists x, P(x) q. The symbol is read as “there exists” q q Bound Variable q. The variable appearing in: Discrete Mathematical Structures: Theory and Applications or

Quantifiers and First Order Logic q Existential Quantifier Example q Consider q It is true since there is at least one real number x for which the proposition is true. Try x=2 q Suppose that P is a propositional function whose domain of discourse consists of the elements d 1, …, dn. The following pseudocode determines whether is true. Discrete Mathematical Structures: Theory and Applications 40

Quantifiers and First Order Logic q Negation of Predicates (De. Morgan’s Laws) q q. Example: q If P(x) is the statement “x has won a race” where the domain of discourse is all runners, then the universal quantification of P(x) is , i. e. , every runner has won a race. The negation of this statement is “it is not the case that every runner has won a race. Therefore there exists at least one runner who has not won a race. Therefore: and so, Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q. Negation of Predicates (De. Morgan’s Laws) q Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Formulas in Predicate Logic q. All statement formulas are considered formulas q. Each n, n =1, 2, . . . , n-place predicate P( ) containing the variables is a formula. q. If A and B are formulas, then the expressions ~A, (A∧B), (A∨B) , A →B and A↔B are statement formulas, where ~, ∧, ∨, → and ↔ are logical connectives q. If A is a formula and x is a variable, then ∀x A(x) and ∃x A(x) are formulas q. All formulas constructed using only above rules are considered formulas in predicate logic Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Additional Rules of Inference q. If the statement ∀x P(x) is assumed to be true, then P(a) is also true, where a is an arbitrary member of the domain of the discourse. This rule is called the universal specification (US) q. If P(a) is true, where a is an arbitrary member of the domain of the discourse, then ∀x P(x) is true. This rule is called the universal generalization (UG) q. If the statement ∃x P (x) is true, then P(a) is true, for some member of the domain of the discourse. This rule is called the existential specification (ES) q. If P(a) is true for some member a of the domain of the discourse, then ∃x P(x) is also true. This rule is called the existential generalization (EG) Discrete Mathematical Structures: Theory and Applications

Quantifiers and First Order Logic q Counterexample q. An argument has the form ∀x (P(x ) → Q(x )), where the domain of discourse is D q. To show that this implication is not true in the domain D, it must be shown that there exists some x in D such that (P(x ) → Q(x )) is not true q. This means that there exists some x in D such that P(x) is true but Q(x) is not true. Such an x is called a counterexample of the above implication q. To show that ∀x (P(x) → Q(x)) is false by finding an x in D such that P(x) → Q(x) is false is called the disproof of the given statement by counterexample Discrete Mathematical Structures: Theory and Applications

Logic and CS q Logic is basis of ALU q Logic is crucial to IF statements q. AND q. OR q. NOT q Implementation of quantifiers q. Looping q Database Query Languages q. Relational Algebra q. Relational Calculus q. SQL Discrete Mathematical Structures: Theory and Applications