Logic Gates 1 Review of Boolean algebra Just

Logic Gates 1

Review of Boolean algebra Just like Boolean logic • Variables can only be 1 or 0 • Instead of true / false – 2

Review of Boolean algebra _ _ Not is a horizontal bar above the number • 0=1 – 1=0 – Or is a plus • 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 1 – – 0*0 = 0 0*1 = 0 1*0 = 0 1*1 = 1 – – And is multiplication • 3

Review of Boolean algebra ___ Example: translate (x+y+z)(xyz) to a Boolean logic • expression (x y z) ( x y z) – We can define a Boolean function: • F(x, y) = (x y) ( x y) – And then write a “truth table” for it: • 4 x y F(x, y) 1 1 0 0 0 1 0 0

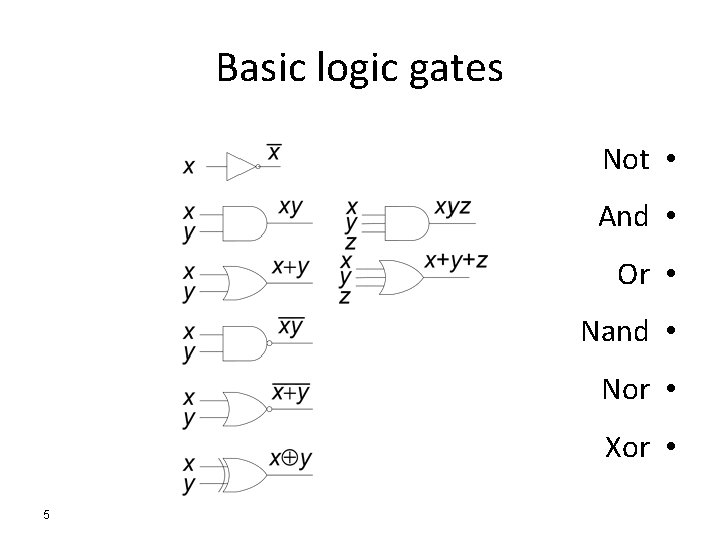
Basic logic gates Not • And • Or • Nand • Nor • Xor • 5

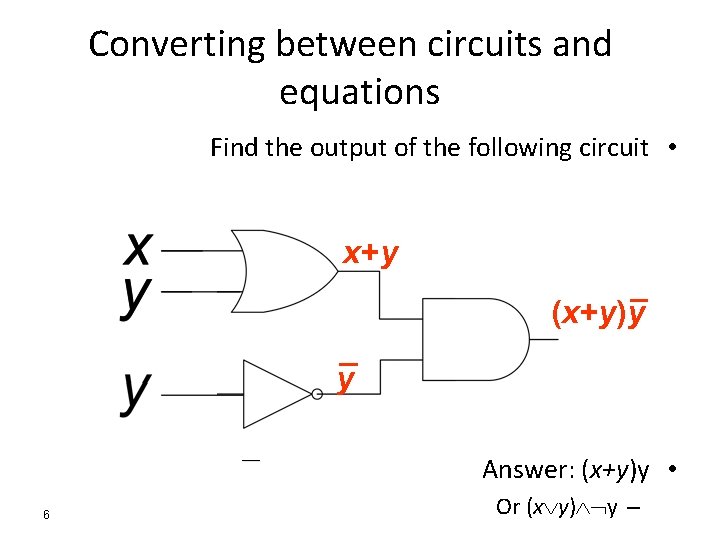
Converting between circuits and equations Find the output of the following circuit • x+ y (x + y )y y __ 6 Answer: (x+y)y • Or (x y) y –

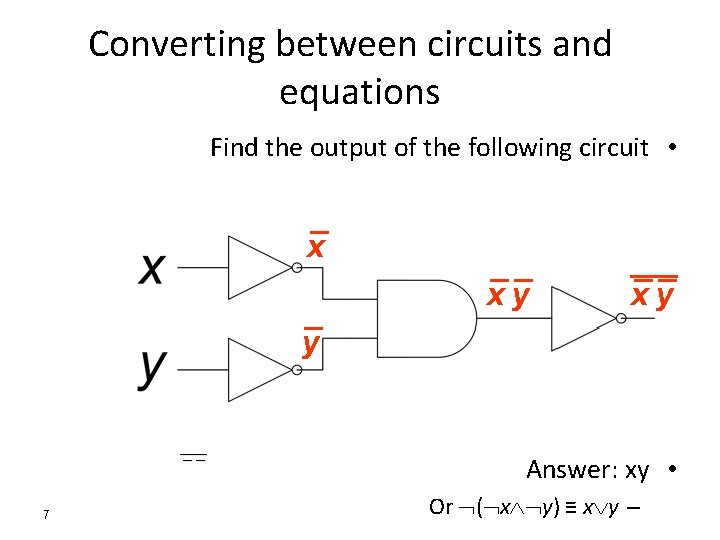
Converting between circuits and equations Find the output of the following circuit • x xy xy y ___ __ 7 Answer: xy • Or ( x y) ≡ x y –

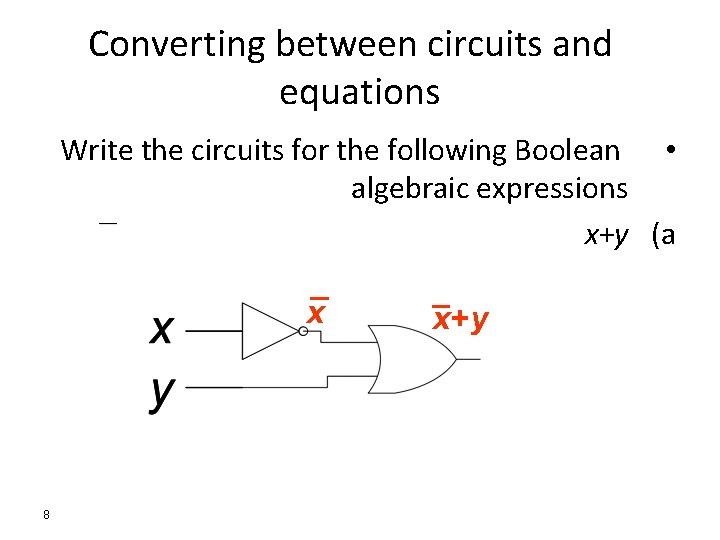
Converting between circuits and equations Write the circuits for the following Boolean • algebraic expressions __ x+y (a x 8 x+ y

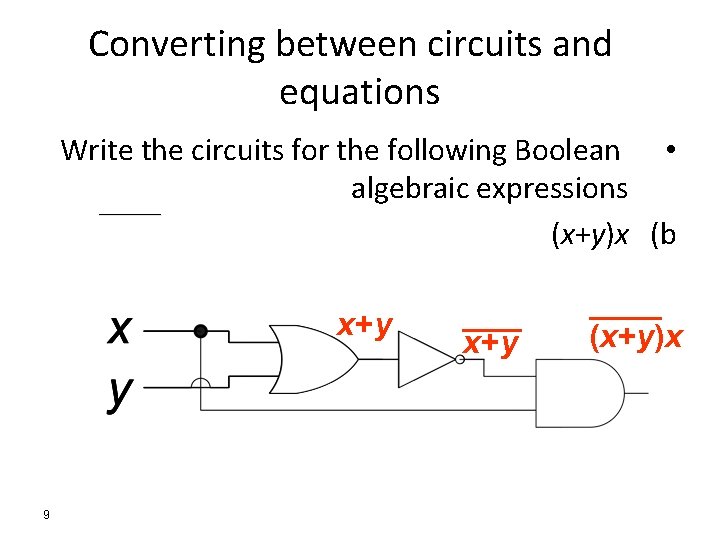
Converting between circuits and equations Write the circuits for the following Boolean • algebraic expressions _______ (x+y)x (b x+ y 9 x+ y (x + y )x

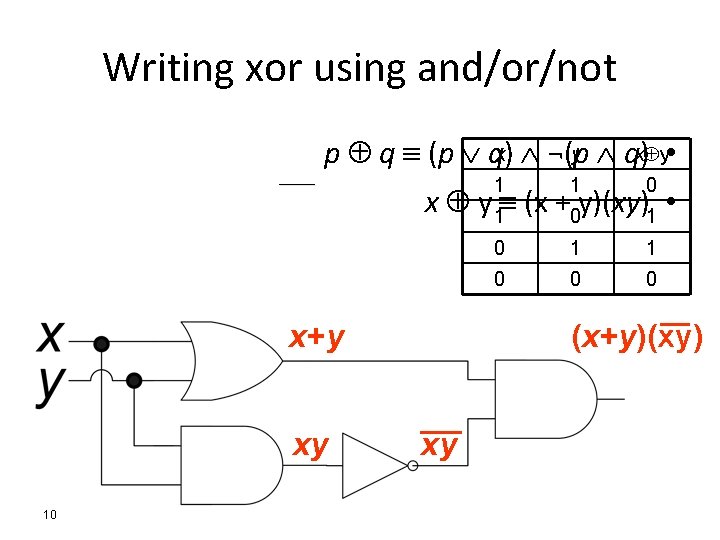
Writing xor using and/or/not ____ p q (p qx) ¬(yp qx y ) • 10 1 0 0 1 1 0 0 0 x y 1 (x +0 y)(xy)1 • x+ y xy 1 (x+y)(xy) xy