Logic for Computer Security Protocols John Mitchell Stanford

Logic for Computer Security Protocols John Mitchell Stanford University

Outline u. Perspective • Math foundations vs computer science u. Motivating example • Floyd-Hoare logic of programs u. Security protocols • Examples of protocols • Toward logics of security protocols

This is a logic conference … u. General properties of logical systems • First-order logic – Model theory • Constructive logic – Proof theory u. Specific theories • Set theory – Large cardinals, independence results, …

“All mathematics is set theory” u. Numbers represented as sets • “There is only one principle of induction, induction on the integers… That’s what the axiom is. ” – P. Cohen u. Every other mathematical thing is represented using sets • Functions, graphs, algebraic structures, geometry (? ), … ? Platonic universe = Set theory

CS View u. Numbers are a special case • Sets are a special case too, but less important since sets are unordered u. Many other important structures • Data structures – Lists, Trees, Graphs, … • Algorithmic concepts – Programs, Functions, Objects, …

Some CS Goals u. General theories • Frameworks for defining and reasoning about computational concepts – Data structures and computations – Numbers and sets could be examples in the framework, but not especially important u. Specific theories • Logic of simple imperative programs • Logic of recursive functional programs • Data type specification and refinement

Disclaimer/Context (Digression) u. Theoretical computer science • Quantitative theory – how many steps – Algorithm design and Complexity theory – Dominant subject in US computer science • Qualitative theory - understand computational universe and its properties – Programming languages and semantics – Logics for specification and verification

Part II Logic of programs Historical references: Floyd, … Hoare, …

Before-after assertions u. Main idea • F <P> G – If F is true before executing P, then G after u. Two variants • Total correctness F [P] G – If F before, then P will halt with G • Partial correctness F {P} G – If F before, and if P halts, then G

While programs u. Programs P : : = x : = e | P; P | if B then P else P | while B do P where x is any variable e is any integer expression B is a Boolean expression (true or false)

Assertion about assignment u. Assignment axiom F(t) { x : = t } F(x) u. Examples 7=7 { x : = 7 } x=7 (y+1)>0 { x : = y+1 } x>0 x+1=2 { x : = x+1 } x=2 This is not most general case. Need to assume no aliasing…

Rule of consequence u. If • F {P}G u. And • F’ F and u. Then • F’ { P } G’ G G’

Example u. Assertion y>0 { x : = y+1 } x>0 u. Proof (y+1)>0 { x : = y+1 } x>0 y>0 { x : = y+1 } x>0 u. Assertion x=1 u. Proof x+1=2 x=1 { x : = x+1 } (assignment axiom) (consequence) x=2 { x : = x+1 } x=2 (assignment axiom) (consequence)

Conditional F B { P 1 } G F B {P 2 } G F { if B then P 1 else P 2 } G u. Example true { if y 0 then x : = y else x : = -y } x 0

Sequence F { P 1 } G G { P 2 } H F { P 1; P 2 } H u. Example x=0 { x : = x+1 ; x : = x+1 } x=2

Loop Invariant F B {P} F F { while B do P } F B u. Example true { while x 0 do x : = x-1 } x=0

Example: Compute d=x-y u. Assertion • P 0 B P 1 y x {d: =0; while (y+d)<x do d : = d+1} y+d=x u. Main ideas in proof • Choose loop invariant y+d x B {P 1} y+d x {while B do P 1} y+d x B • Use assignment axiom and sequence rule to complete the proof of property of P 1

Facts about Hoare logic u. Compositional • Proof follows structure of program u. Sound u“Relative completeness” • Properties of computation over N provable from properties of N • Some technical issues … u. Important concept: Loop invariant !!! • Common practice beyond Hoare logic

Part III Protocol Examples Warning: bait and switch

Contract signing Immunity deal u. Both parties want to sign a contract u. Neither wants to commit first

General protocol outline I am going to sign the contract A Here is my signature B Here is my signature u. Trusted third party can force contract • Third party can declare contract binding if presented with first two messages.

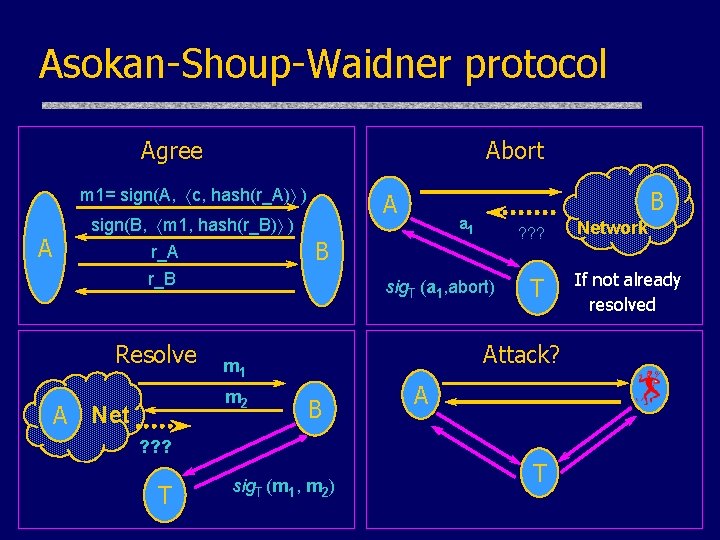
Asokan-Shoup-Waidner protocol Agree Abort m 1= sign(A, c, hash(r_A) ) A sign(B, m 1, hash(r_B) ) r_A A Resolve ? ? ? sig. T (a 1, abort) T Attack? m 1 m 2 A Net a 1 B r_B B B A ? ? ? T sig. T (m 1, m 2) T Network If not already resolved

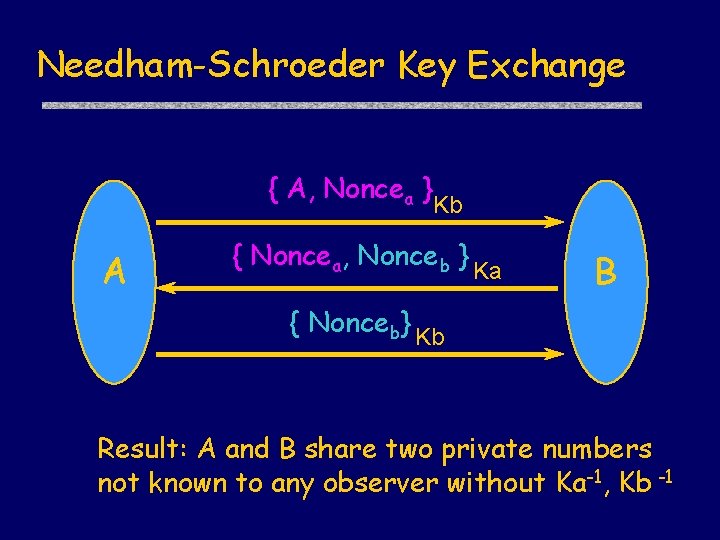
Needham-Schroeder Key Exchange { A, Noncea } A Kb { Noncea, Nonceb } Ka B { Nonceb} Kb Result: A and B share two private numbers not known to any observer without Ka-1, Kb -1

Anomaly in Needham-Schroeder [Lowe] { A, Na } Ke A E { Na, Nb }Ka { Nb }Ke Evil agent E tricks honest A into revealing private key Nb from B. Evil E can then fool B. { A, Na } { N a, N b } Ka B Kb

Analysis Methods u. Simplified model • Exhaustive search methods – Limited to finite model • Grungy proof methods based on traces – Isabelle, etc; • Attempts to identify reasoning methods u. Not so simple model • Ad hoc proofs • Attempts to identify reasoning methods

Part IV A Logic for Security Protocols work with N. Durgin, D. Pavlovic

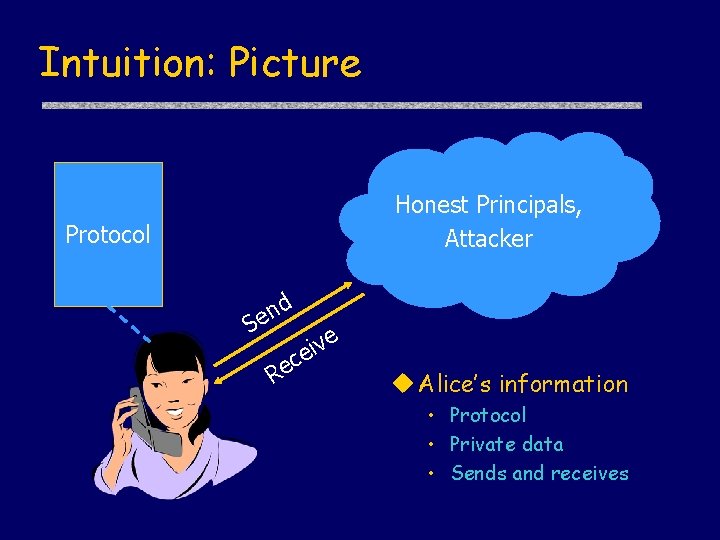
Intuition u. Reason about local information • • I chose a new number I sent it out encrypted I received it decrypted Therefore: someone decrypted it u. Incorporate knowledge about protocol • Protocol: Server only sends m if sent m’ • If server not corrupt and I receive m signed by server, then server received m’

Intuition: Picture Honest Principals, Attacker Protocol nd e S c e R e v i e u Alice’s information • Protocol • Private data • Sends and receives

Logical assertions u. Modal operator • [ actions ] P - after actions, P reasons u. Predicates in • • Sent(X, m) - principal X sent message m Created(X, m) – X assembled m from parts Decrypts(X, m) - X has m and key to decrypt m Knows(X, m) - X created m or received msg containing m and has keys to extract m from msg • Source(m, X, S) – Y X can only learn m from set S • Honest(X) – X follows rules of protocol

Semantics u. Protocol Q • Defines set of roles (e. g, initiator, responder) • Run R of Q is sequence of actions by principals following roles, plus attacker u. Satisfaction • Q, R | [ actions ] P Some role of P in R does exactly actions and is true in state after actions completed • Q | [ actions ] P Q, R | [ actions ] P for all runs R of Q Formula is [ actions ] P where has no [ …] P’

Sample axioms about actions u. New data • [ new x ]P Knows(P, x) • [ new x ]P Knows(Y, x) Y=P u. Send • [ send m ]P Sent(P, m) u. Receive • [recv m]P Knows(P, m) u. Decyption • [x : = decrypt(k, encrypt(k, m))]P Decrypts(P, encrypt(k, m))

Reasoning about “Knows” u. Pairing • Knows(X, m, n ) Knows(X, m) Knows(X, n) u. Encryption • Knows(X, encrypt(k, m)) Knows(X, k-1) Knows(X, m)

Source predicate u. New data • [ new x ]P Source(x, P, { }) u. Message [ acts ]P Source(x, Q, S) [ acts; send m]P Source(x, Q, S {m}) u. Reasoning • Source{m, X, { encrypt(k, m) }) Knows(Y, m) Y X Z. Decrypts(Z, encrypt(k, m) )

Bidding conventions (motivation) u. Blackwood response to 4 NT – 5§ : – 5¨ : – 5© : – 5ª : 0 or 4 aces 1 ace 2 aces 3 aces u. Reasoning • If my partner is following Blackwood, then if she bid 5©, she must have 2 aces

Honesty rule (rule scheme) roles R of Q. initial segments A R. Q |- [ A ]X Q |- Honest(X) • This is a finitary rule: – Typical protocol has 2 -3 roles – Typical role has 1 -3 receives – Only need to consider A waiting to receive

Honesty hypotheses for NSL [ new m; send encrypt( Key(Y), X, m ) ]X [ new m; send encrypt( Key(Y), X, m ); recv encrypt( Key(X), m, B, n ); send encrypt( Key(B), n ) ]X send encrypt( Key(Y), m, X, n ) ]X [ recv encrypt( Key(X), Y, m ); new n; [ recv encrypt( Key(B), A, m ); new n; send encrypt( Key(A), m, B, n ); recv encrypt( Key(B), n ) ]X “Alice” “Bob”

Honesty rule (example use) roles R of Q. initial segments A R. Q |- [ A ]X Q |- Honest(X) • Example use: – If Y receives a message from X, and Honest(X) (Sent(X, m) Received(X, m’)) then Y can conclude Honest(X) Received(X, m’))

Benchmarks u. Can prove repaired NSL protocol u. Proof fails for original NS protocol

Correctness of NSL u. Bob knows he’s talking to Alice [ recv encrypt( Key(B), A, m ); new n; msg 1 send encrypt( Key(A), m, B, n ); recv encrypt( Key(B), n ) ]B msg 3 Honest(A) Csent(A, msg 1) Csent(A, msg 3) where Csent(A, …) Created(A, …) Sent(A, …)

Proof uses “honesty rule” u. Consequent of honesty rule Honest(A) Decrypts(A, encrypt( Key(A), m, B, n )) Csent(A, msg 1) Csent(A, msg 3) The implication Decrypts(X, …) Csent(X, …) is an invariant of the protocol. It is true at each waiting state of each role X.

Initiator role OK for NS, NSL u. Alice wants similar conclusions, e. g. , [ new m; send encrypt( Key(B), A, m ); recv encrypt( Key(A), m, B, n ); send encrypt( Key(B), n ) ]A Honest(B) Csent(B, msg 2)

Proof uses “honesty rule” u. Consequent of honesty rule Honest(X) Csent(X, encrypt( Key(Y), m, Z, n ) X=Z • FIX THIS !!! Do not use slide as is!

Failure for “buggy” NS u. Bob hopes he’s talking to Alice [ recv encrypt( Key(B), A, m ); new n; m 1(B) send encrypt( Key(A), m, B, n ); recv encrypt( Key(B), n ) ]B m 3(B) Honest(A) Csent(A, m 1(B)) Csent(A, m 3(B)) where Csent(A, …) Created(A, …) Sent(A, …)

Attempt use of “honesty rule” u. Protocol invariant Honest(A) Decrypts(A, encrypt( Key(A), m, B, n )) Csent(A, m 1(Z)) Csent(A, m 3(Z)) Cannot prove Z=B

Status of this logic u. Just starting • This is a first attempt at a style of protocol logic u. Lots more to do • Work out more examples • Simplify the formalism – Express Created using Knows and Sent, Decrypts using Knows, … • Refine the proof rules, semantics • Make sure others can use this

Conclusion u. Computer security is good application • People care about correctness • Cryptography understood, usage less so u. Security protocols • Simple distributed programs • Complexity comes from possible attacks u. Proposed protocol logic • Hide behavior of attacker in model • Identify concepts that give understanding