Logic Design Review 2 Basic Combinational Circuits Lecture

Logic Design Review – 2 Basic Combinational Circuits Lecture L 14. 2 Verilog

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

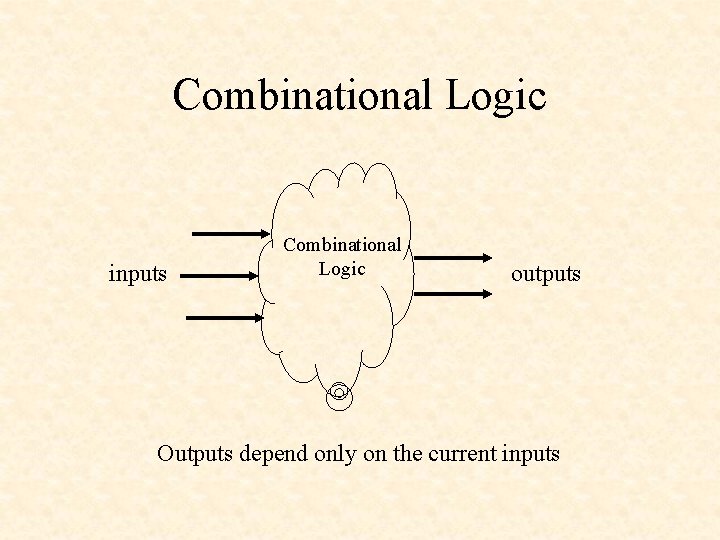
Combinational Logic inputs Combinational Logic outputs Outputs depend only on the current inputs

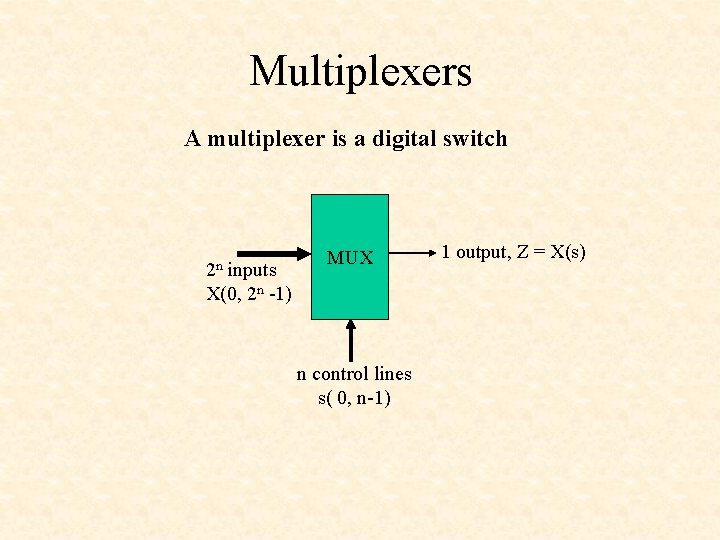
Multiplexers A multiplexer is a digital switch 2 n inputs X(0, 2 n -1) MUX n control lines s( 0, n-1) 1 output, Z = X(s)

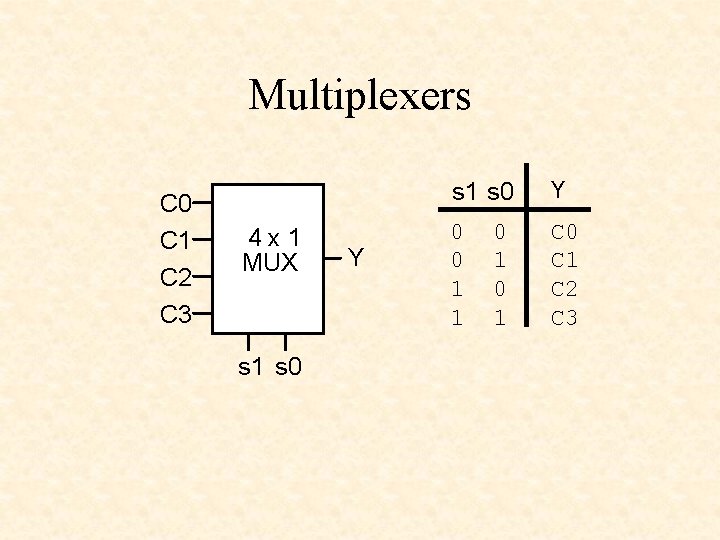
Multiplexers C 0 C 1 C 2 C 3 4 x 1 MUX s 1 s 0 Y 0 0 1 1 C 0 C 1 C 2 C 3 0 1

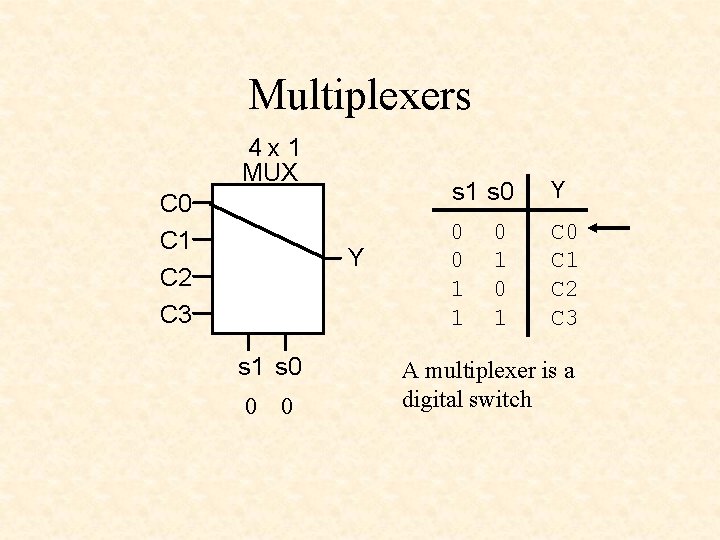
Multiplexers 4 x 1 MUX C 0 C 1 C 2 C 3 Y s 1 s 0 0 0 s 1 s 0 Y 0 0 1 1 C 0 C 1 C 2 C 3 0 1 A multiplexer is a digital switch

Multiplexers 4 x 1 MUX C 0 C 1 C 2 C 3 Y s 1 s 0 0 1 s 0 Y 0 0 1 1 C 0 C 1 C 2 C 3 0 1

Multiplexers 4 x 1 MUX C 0 C 1 C 2 C 3 Y s 1 s 0 1 0 s 1 s 0 Y 0 0 1 1 C 0 C 1 C 2 C 3 0 1

Multiplexers 4 x 1 MUX C 0 C 1 C 2 C 3 Y s 1 s 0 1 1 s 0 Y 0 0 1 1 C 0 C 1 C 2 C 3 0 1

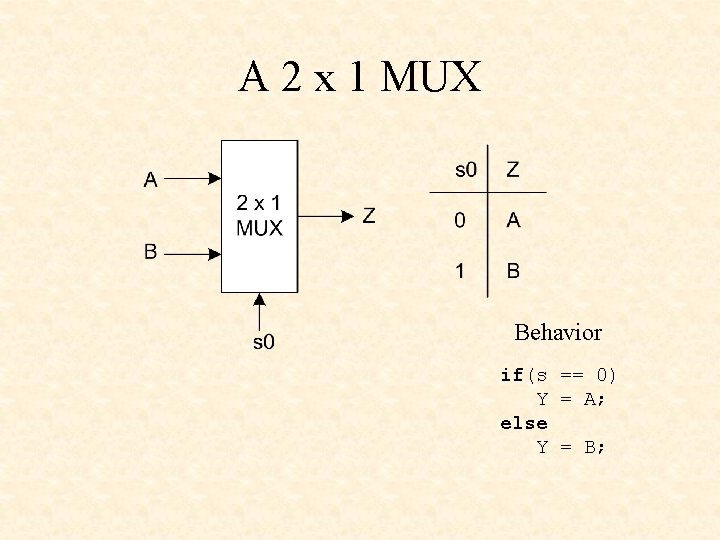
A 2 x 1 MUX Behavior if(s == 0) Y = A; else Y = B;

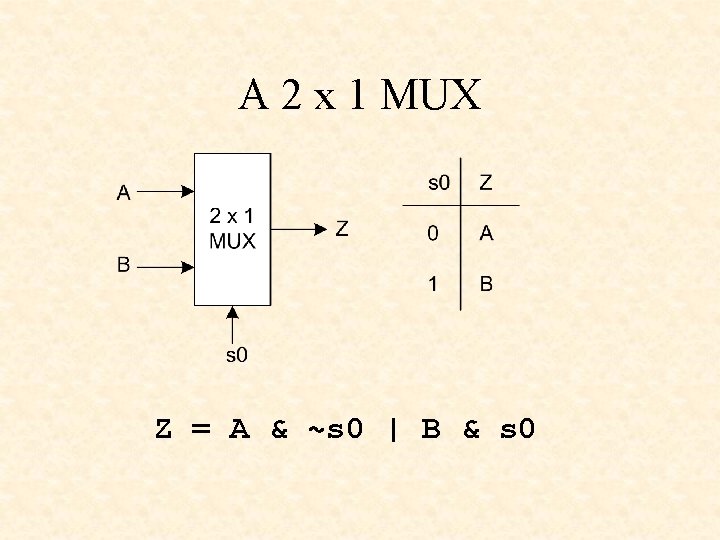
A 2 x 1 MUX Z = A & ~s 0 | B & s 0

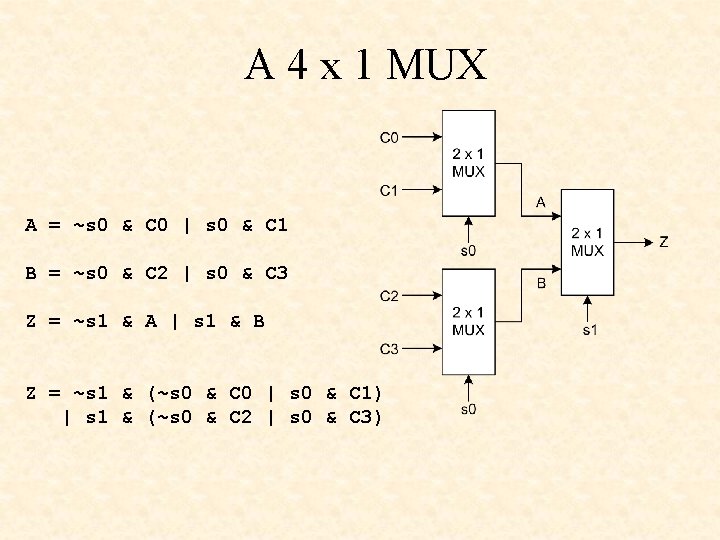
A 4 x 1 MUX A = ~s 0 & C 0 | s 0 & C 1 B = ~s 0 & C 2 | s 0 & C 3 Z = ~s 1 & A | s 1 & B Z = ~s 1 & (~s 0 & C 0 | s 0 & C 1) | s 1 & (~s 0 & C 2 | s 0 & C 3)

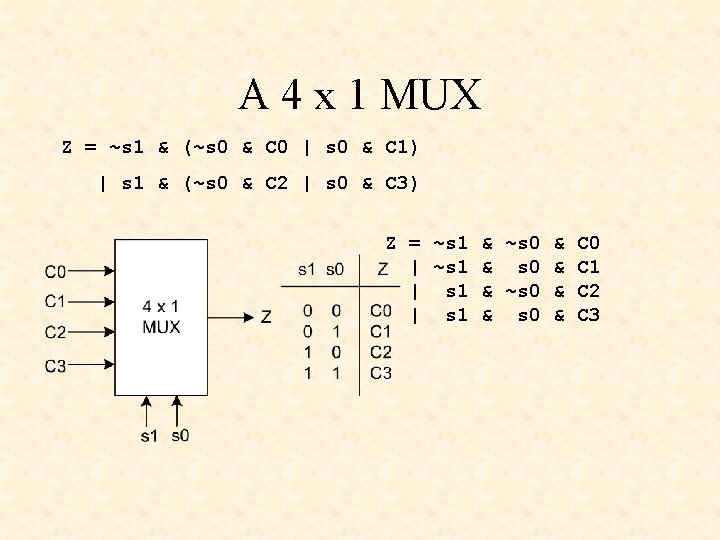
A 4 x 1 MUX Z = ~s 1 & (~s 0 & C 0 | s 0 & C 1) | s 1 & (~s 0 & C 2 | s 0 & C 3) Z = ~s 1 & ~s 0 & | ~s 1 & s 0 & | s 1 & ~s 0 & | s 1 & s 0 & C 0 C 1 C 2 C 3

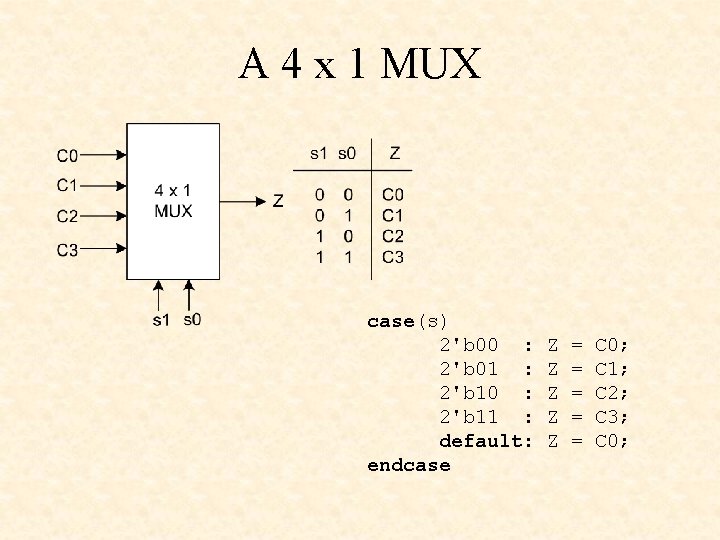
A 4 x 1 MUX case(s) 2'b 00 : 2'b 01 : 2'b 10 : 2'b 11 : default: endcase Z Z Z = = = C 0; C 1; C 2; C 3; C 0;

Problem How would you make a Quad 2 -to-1 MUX? [A 3. . A 0] [B 3. . B 0] Quad 2 -to-1 MUX s [Y 3. . Y 0] s Y 0 1 A B

mux. v module mux 24(A, B, s, Y); input [3: 0] A; input [3: 0] B; input s; output [3: 0] Y; wire [3: 0] Y; assign Y = {4{~s}} & A | {4{s}} & B; endmodule [A 3. . A 0] [B 3. . B 0] Quad 2 -to-1 MUX s [Y 3. . Y 0]

module mux 24(A, B, s, Y); input [3: 0] A; input [3: 0] B; input s; output [3: 0] Y; wire [3: 0] Y; assign Y = {4{~s}} & A | {4{s}} & B; endmodule

mux. v module mux 24 a(A, B, s, Y); input [3: 0] A; input [3: 0] B; input s; output [3: 0] Y; reg [3: 0] Y; always @(A, B, s) if(s == 0) Y = A; else Y = B; endmodule [A 3. . A 0] [B 3. . B 0] Quad 2 -to-1 MUX s [Y 3. . Y 0]

module mux 24 a(A, B, s, Y); input [3: 0] A; input [3: 0] B; input s; output [3: 0] Y; reg [3: 0] Y; always @(A, B, s) if(s == 0) Y = A; else Y = B; endmodule

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

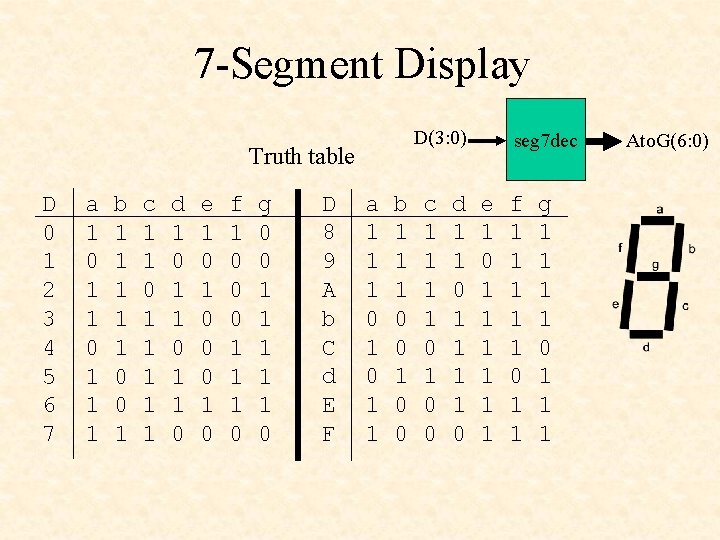
7 -Segment Display D(3: 0) Truth table D 0 1 2 3 4 5 6 7 a 1 0 1 1 1 b 1 1 1 0 0 1 c 1 1 0 1 1 1 d 1 0 1 1 0 e 1 0 0 0 1 0 f 1 0 0 0 1 1 1 0 g 0 0 1 1 1 0 D 8 9 A b C d E F a 1 1 1 0 1 1 b 1 1 1 0 0 c 1 1 0 1 0 0 d 1 1 0 seg 7 dec e 1 0 1 1 1 f 1 1 1 0 1 1 g 1 1 0 1 1 1 Ato. G(6: 0)

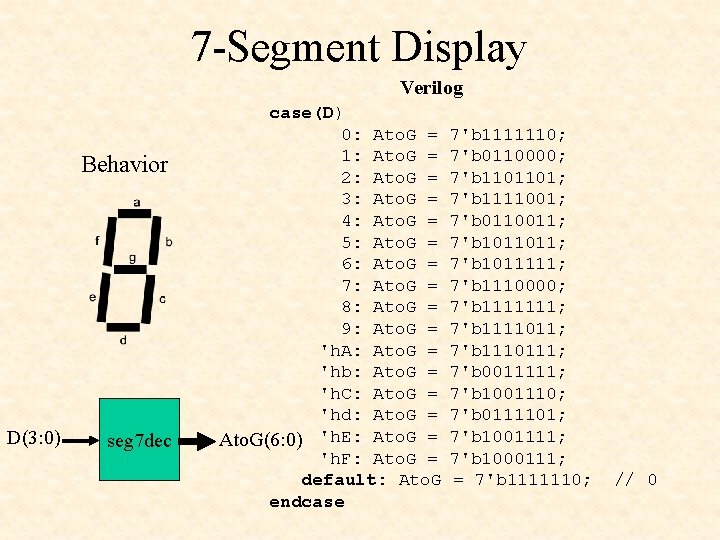
7 -Segment Display Verilog Behavior D(3: 0) seg 7 dec case(D) 0: Ato. G = 1: Ato. G = 2: Ato. G = 3: Ato. G = 4: Ato. G = 5: Ato. G = 6: Ato. G = 7: Ato. G = 8: Ato. G = 9: Ato. G = 'h. A: Ato. G = 'hb: Ato. G = 'h. C: Ato. G = 'hd: Ato. G = Ato. G(6: 0) 'h. E: Ato. G = 'h. F: Ato. G = default: Ato. G endcase 7'b 1111110; 7'b 0110000; 7'b 1101101; 7'b 1111001; 7'b 0110011; 7'b 1011111; 7'b 1110000; 7'b 1111111; 7'b 1111011; 7'b 1110111; 7'b 0011111; 7'b 1001110; 7'b 0111101; 7'b 1001111; 7'b 1000111; = 7'b 1111110; // 0

module hex 7 seg(D, Ato. G); input [3: 0] D; output [6: 0] Ato. G; reg [6: 0] Ato. G; always @(D) case(D) 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 'h. A: 'hb: 'h. C: 'hd: 'h. E: 'h. F: default: endcase endmodule hex 7 seg. v Verilog Ato. G Ato. G = = = = = 7'b 1111110; 7'b 0110000; 7'b 1101101; 7'b 1111001; 7'b 0110011; 7'b 1011111; 7'b 1110000; 7'b 1111111; 7'b 1111011; 7'b 1110111; 7'b 0011111; 7'b 1001110; 7'b 0111101; 7'b 1001111; 7'b 1000111; 7'b 1111110; a f b g e c d // 0

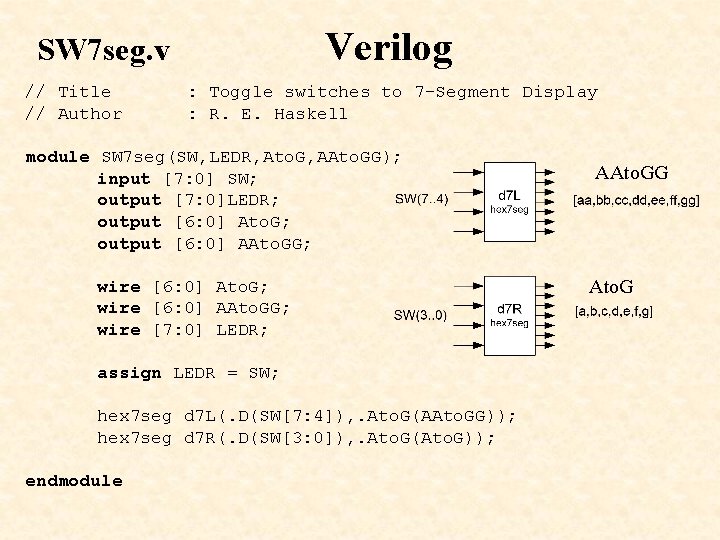
Verilog SW 7 seg. v // Title // Author : Toggle switches to 7 -Segment Display : R. E. Haskell module SW 7 seg(SW, LEDR, Ato. G, AAto. GG); input [7: 0] SW; output [7: 0]LEDR; output [6: 0] Ato. G; output [6: 0] AAto. GG; wire [6: 0] Ato. G; wire [6: 0] AAto. GG; wire [7: 0] LEDR; assign LEDR = SW; hex 7 seg d 7 L(. D(SW[7: 4]), . Ato. G(AAto. GG)); hex 7 seg d 7 R(. D(SW[3: 0]), . Ato. G(Ato. G)); endmodule AAto. GG Ato. G

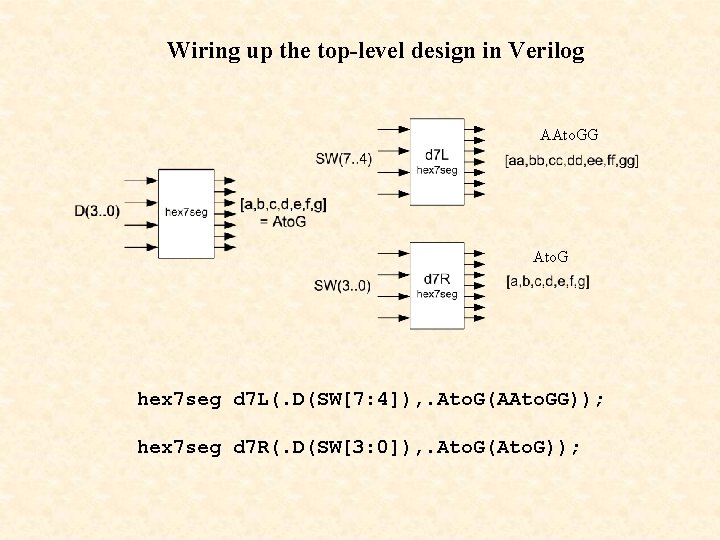
Wiring up the top-level design in Verilog AAto. GG Ato. G hex 7 seg d 7 L(. D(SW[7: 4]), . Ato. G(AAto. GG)); hex 7 seg d 7 R(. D(SW[3: 0]), . Ato. G(Ato. G));

#PACE: Start of PACE I/O Pin Assignments NET "AAto. GG<0>" LOC = "p 66" ; NET "AAto. GG<1>" LOC = "p 65" ; NET "AAto. GG<2>" LOC = "p 63" ; NET "AAto. GG<3>" LOC = "p 62" ; NET "AAto. GG<4>" LOC = "p 61" ; NET "AAto. GG<5>" LOC = "p 58" ; NET "AAto. GG<6>" LOC = "p 57" ; NET "Ato. G<0>" LOC = "p 17" ; NET "Ato. G<1>" LOC = "p 14" ; NET "Ato. G<2>" LOC = "p 19" ; NET "Ato. G<3>" LOC = "p 21" ; NET "Ato. G<4>" LOC = "p 23" ; NET "Ato. G<5>" LOC = "p 18" ; NET "Ato. G<6>" LOC = "p 15" ; NET "LEDR<0>" LOC = "p 44" ; NET "LEDR<1>" LOC = "p 43" ; NET "LEDR<2>" LOC = "p 41" ; NET "LEDR<3>" LOC = "p 40" ; NET "LEDR<4>" LOC = "p 39" ; NET "LEDR<5>" LOC = "p 37" ; NET "LEDR<7>" LOC = "p 35" ; NET "SW<0>" LOC = "p 1" ; NET "SW<1>" LOC = "p 2" ; NET "SW<2>" LOC = "p 3" ; NET "SW<3>" LOC = "p 4" ; NET "SW<4>" LOC = "p 5" ; NET "SW<5>" LOC = "p 6" ; NET "SW<6>" LOC = "p 7" ; NET "SW<7>" LOC = "p 11" ; SW 7 seg. ucf

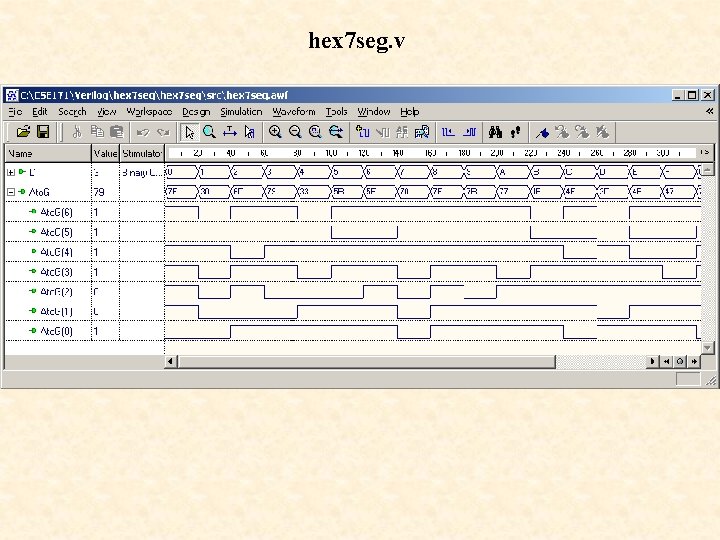
hex 7 seg. v

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

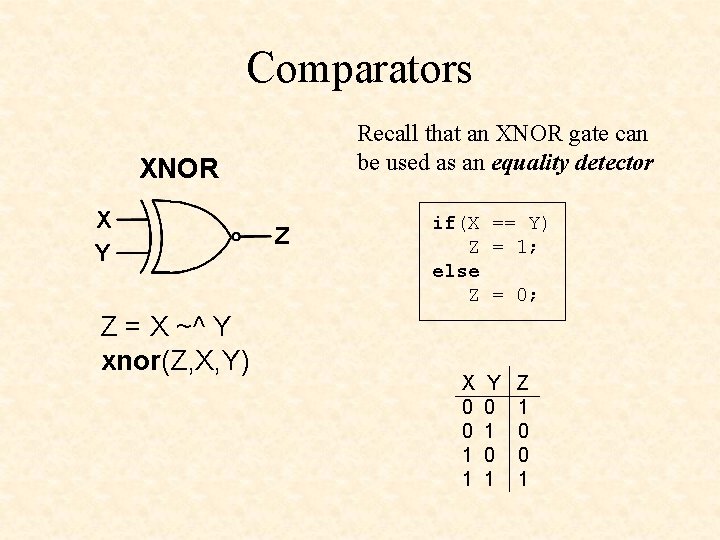
Comparators Recall that an XNOR gate can be used as an equality detector XNOR X Y Z = X ~^ Y xnor(Z, X, Y) Z if(X == Y) Z = 1; else Z = 0; X 0 0 1 1 Y 0 1 Z 1 0 0 1

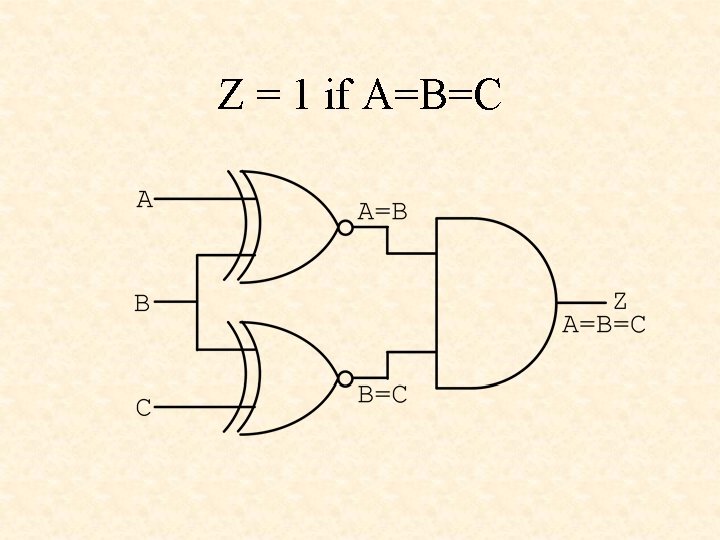
Z = 1 if A=B=C

A 1 -Bit Comparator The variable Gout is 1 if x > y or if x = y and Gin = 1. The variable Eout is 1 if x = y and Gin = 0 and Lin = 0. The variable Lout is 1 if x < y or if x = y and Lin = 1.

The variable Gout is 1 if x > y or if x = y and Gin = 1. The variable Eout is 1 if x = y and Gin = 0 and Lin = 0. The variable Lout is 1 if x < y or if x = y and Lin = 1.

Gout = x & ~y | x & Gin | ~y & Gin Eout = ~x & ~y & ~Gin & ~Lin | x & y & ~Gin & ~Lin Lout = ~x & y | ~x & Lin | y & Lin

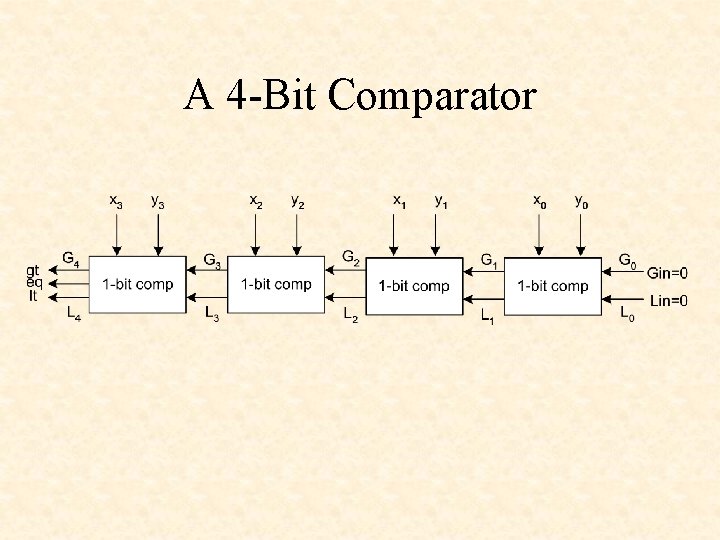
A 4 -Bit Comparator

Comparators A[3: 0] A_EQ_B comp B[3: 0] A_GT_B A_LT_B

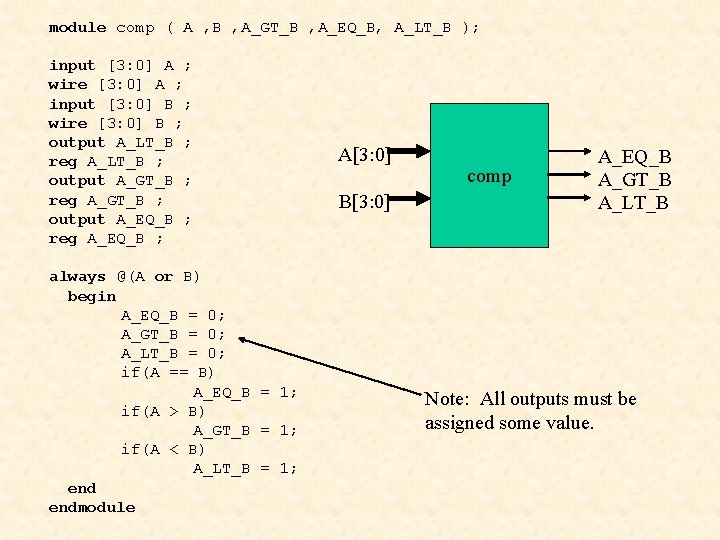
module comp ( A , B , A_GT_B , A_EQ_B, A_LT_B ); input [3: 0] A ; wire [3: 0] A ; input [3: 0] B ; wire [3: 0] B ; output A_LT_B ; reg A_LT_B ; output A_GT_B ; reg A_GT_B ; output A_EQ_B ; reg A_EQ_B ; always @(A or B) begin A_EQ_B = 0; A_GT_B = 0; A_LT_B = 0; if(A == B) A_EQ_B = 1; if(A > B) A_GT_B = 1; if(A < B) A_LT_B = 1; endmodule A[3: 0] B[3: 0] comp A_EQ_B A_GT_B A_LT_B Note: All outputs must be assigned some value.

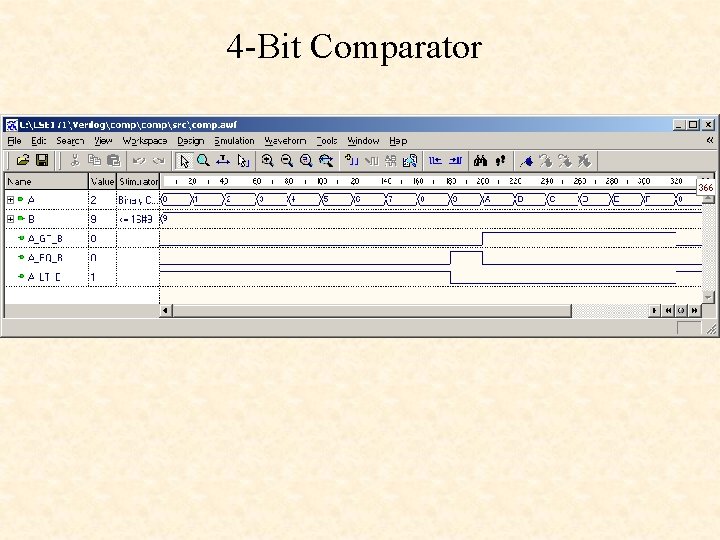
4 -Bit Comparator

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

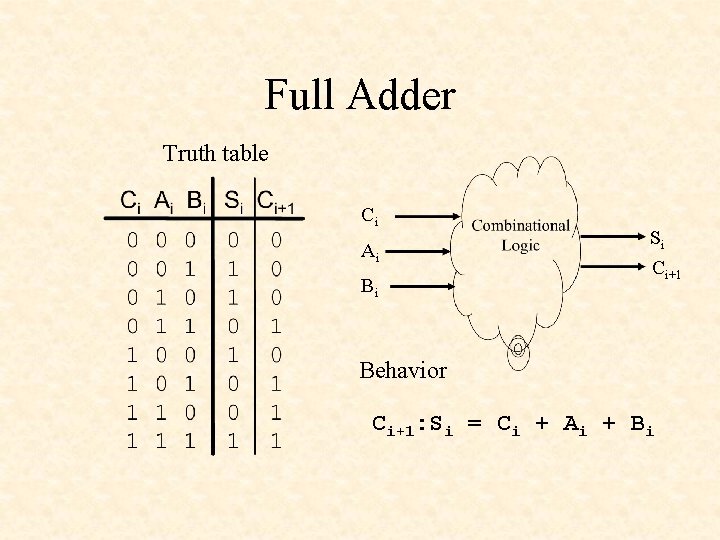
Full Adder Truth table Ci Ai Bi Si Ci+1 Behavior Ci+1: Si = Ci + Ai + Bi

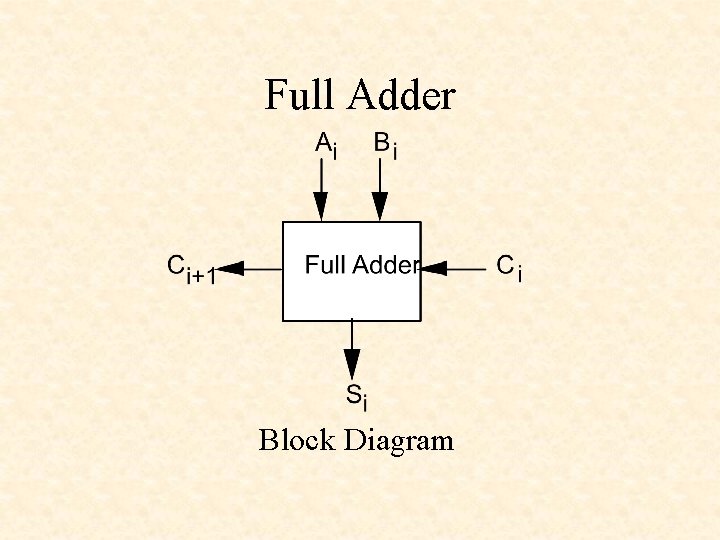
Full Adder Block Diagram

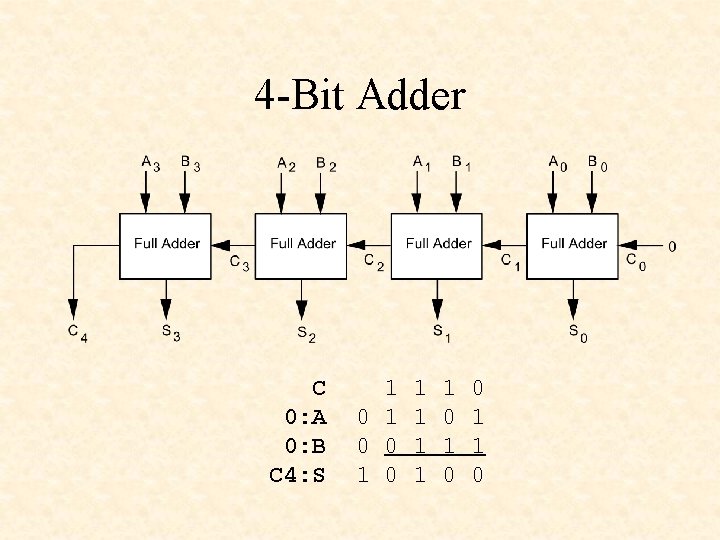
4 -Bit Adder C 0: A 0: B C 4: S 1 0 0 1 1 1 0 1 0 0 1 1 0

module adder 4(A, B, S, carry); input [3: 0] A; input [3: 0] B; output [3: 0] S; output carry; reg [3: 0] S; reg carry; reg [4: 0] temp; adder. v Note: In the sensitivity list a comma can be used in place of or in Verilog 2001 always @(A, B) begin temp = {1'b 0, A} + {1'b 0, B}; S = temp[3: 0]; carry = temp[4]; Concatenate a leading 0 endmodule

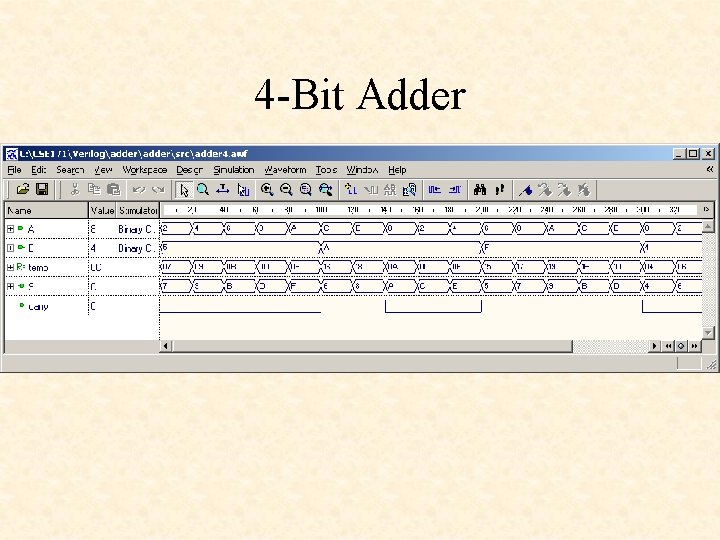
4 -Bit Adder

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

3 -to-8 Decoder input [2: 0] A ; wire [2: 0] A ; Behavior for(i = 0; i <= 7; i = i+1) if(A == i) Y[i] = 1; else Y[i] = 0; output [0: 7] Y ; reg [0: 7] Y ;

decode 38. v 3 -to-8 Decoder module decode 38 ( A, Y ); input [2: 0] A ; wire [2: 0] A ; output [0: 7] Y ; reg [0: 7] Y ; integer i; always @(A) for(i = 0; i <= 7; i = i+1) if(A == i) Y[i] = 1; else Y[i] = 0; endmodule

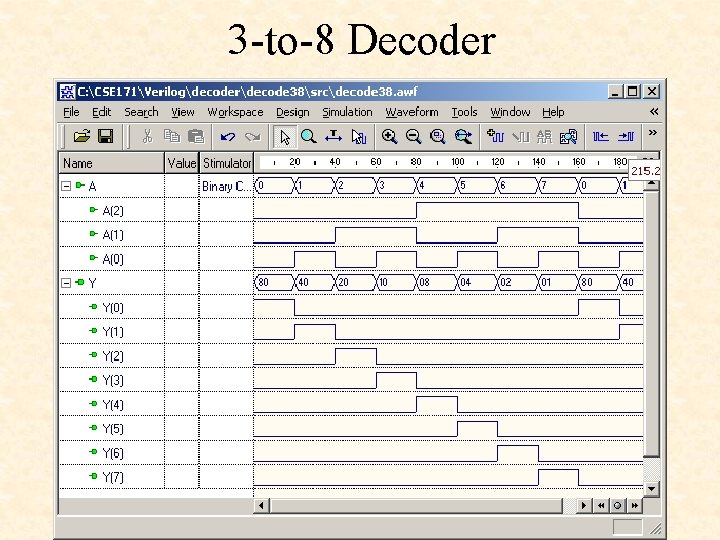
3 -to-8 Decoder

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

Gray Code Definition: An ordering of 2 n binary numbers such that only one bit changes from one entry to the next. Binary coding {0. . . 7}: {000, 001, 010, 011, 100, 101, 110, 111} Gray coding {0. . . 7}: {000, 001, 010, 111, 100} Not unique One method for generating a Gray code sequence: Start with all bits zero and successively flip the right-most bit that produces a new string.

Binary - Gray Code Conversions Gray code: G[i], i = n – 1 : 0 Binary code: B[i], i = n – 1 : 0 Binary coding {0. . . 7}: {000, 001, 010, 011, 100, 101, 110, 111} Gray coding {0. . . 7}: {000, 001, 010, 111, 100} Convert Binary to Gray: Copy the most significant bit. For each smaller i G[i] = B[i+1] ^ B[i] Convert Gray to Binary: Copy the most significant bit. For each smaller i B[i] = B[i+1] ^ G[i]

bin 2 gray. v module bin 2 gray ( B , G ); input [3: 0] B ; wire [3: 0] B ; output [3: 0] G ; wire [3: 0] G ; assign G[3] = B[3]; assign G[2: 0] = B[3: 1] ^ B[2: 0]; endmodule Convert Binary to Gray: Copy the most significant bit. For each smaller i G[i] = B[i+1] ^ B[i]

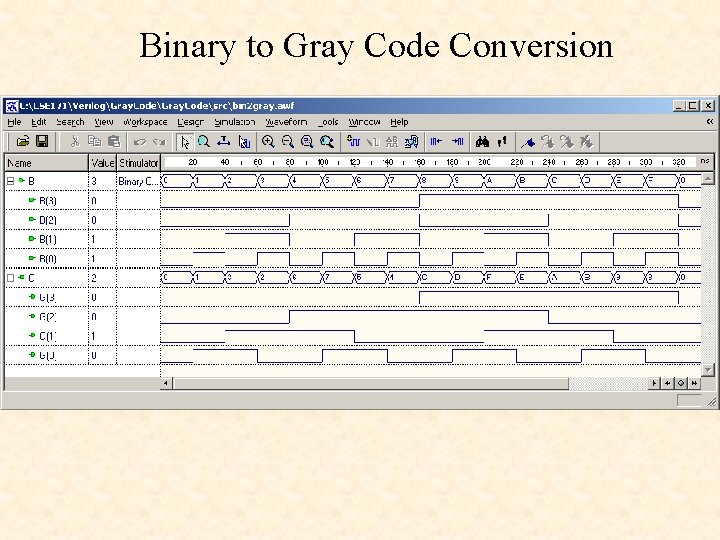
Binary to Gray Code Conversion

gray 2 bin. v module gray 2 bin ( G , B ); input [3: 0] G ; wire [3: 0] G ; output [3: 0] B ; reg [3: 0] B ; integer i; Convert Gray to Binary: Copy the most significant bit. For each smaller i B[i] = B[i+1] ^ G[i] always @(G) begin B[3] = G[3]; for(i=2; i >= 0; i = i-1) B[i] = B[i+1] ^ G[i]; endmodule

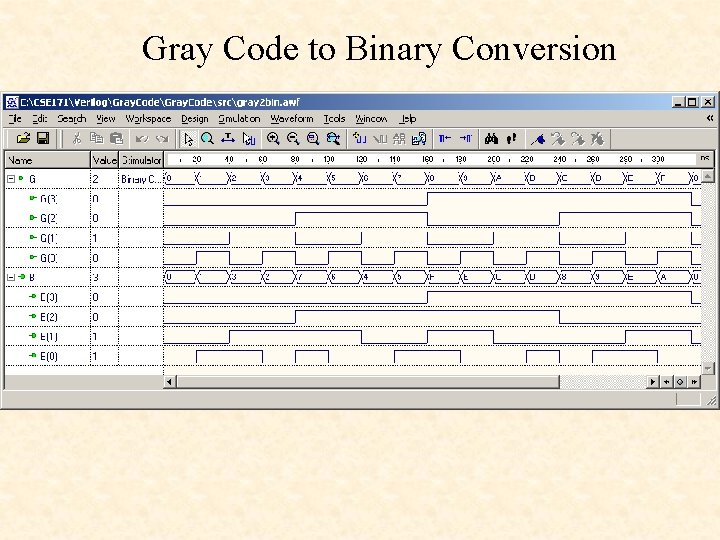
Gray Code to Binary Conversion

Basic Combinational Circuits • • • Multiplexers 7 -Segment Decoder Comparators Adders Decoders Code Converters – Gray Code Converter – Binary-to-BCD Converter

Binary-to-BCD Conversion • Shift and add 3 algorithm • RTL solution • Behavioral solution

Shift and Add-3 Algorithm 11. 22. 33. 44. Shift the binary number left one bit. If 8 shifts have taken place, the BCD number is in the Hundreds, Tens, and Units column. If the binary value in any of the BCD columns is 5 or greater, add 3 to that value in that BCD column. Go to 1.

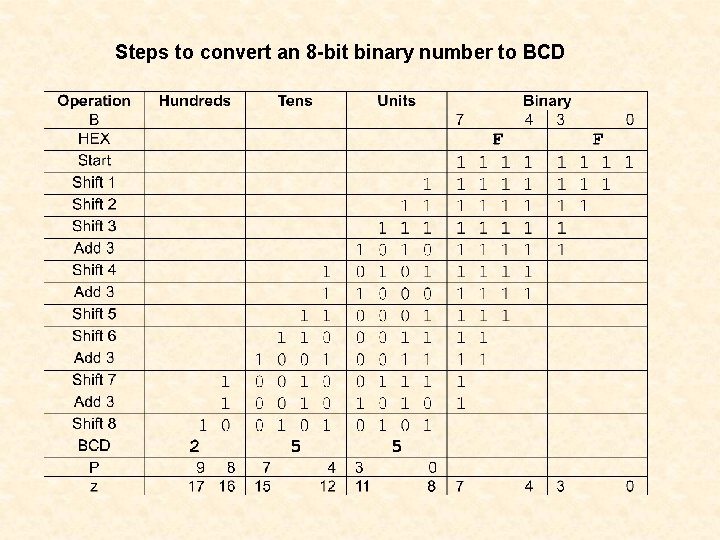
Steps to convert an 8 -bit binary number to BCD

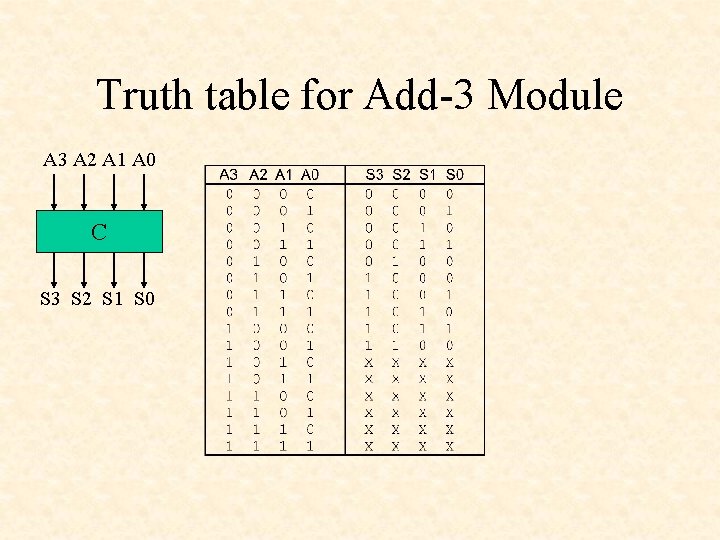
Truth table for Add-3 Module A 3 A 2 A 1 A 0 C S 3 S 2 S 1 S 0

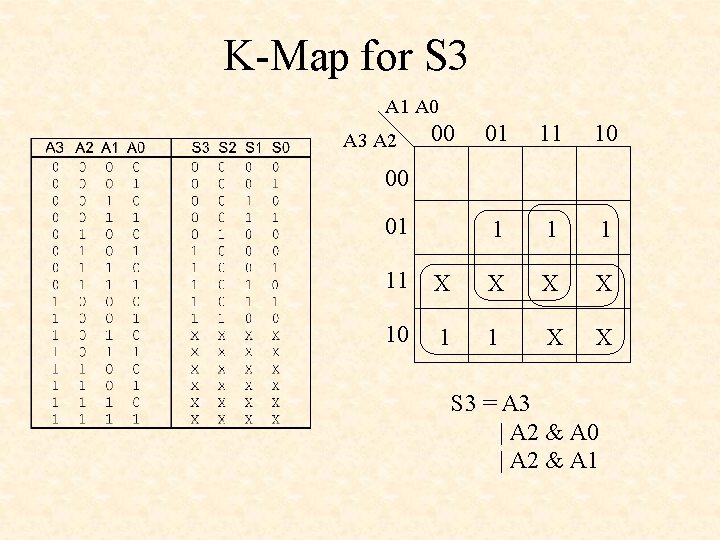
K-Map for S 3 A 1 A 0 A 3 A 2 00 01 11 10 1 1 1 00 01 11 X X 10 1 1 X X S 3 = A 3 | A 2 & A 0 | A 2 & A 1

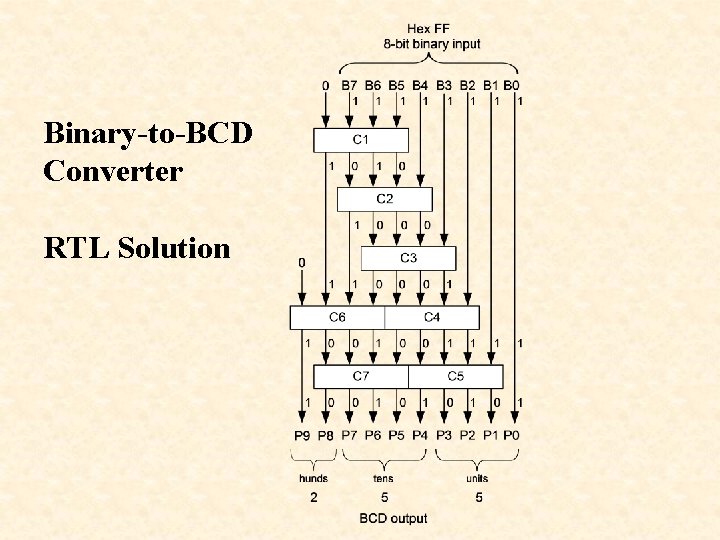
Binary-to-BCD Converter RTL Solution

Steps to convert a 6 -bit binary number to BCD 1. Clear all bits of z to zero 2. Shift B left 3 bits z[8: 3] = B[5: 0]; 3. Do 3 times if Units >4 then add 3 to Units (note: Units = z[9: 6]) Shift z left 1 bit 4. Tens = P[6: 4] = z[12: 10] Units = P[3: 0] = z[9: 6]

module binbcd 6(B, P); input [5: 0] B; output [6: 0] P; reg [12: 0] z; integer i; binbcd 6. v always @(B) begin for(i = 0; i <= 12; i = i+1) z[i] = 0; z[8: 3] = B; for(i = 0; i <= 2; i = i+1) begin if(z[9: 6] > 4) z[9: 6] = z[9: 6] + 3; z[12: 1] = z[11: 0]; end P = z[12: 6]; endmodule

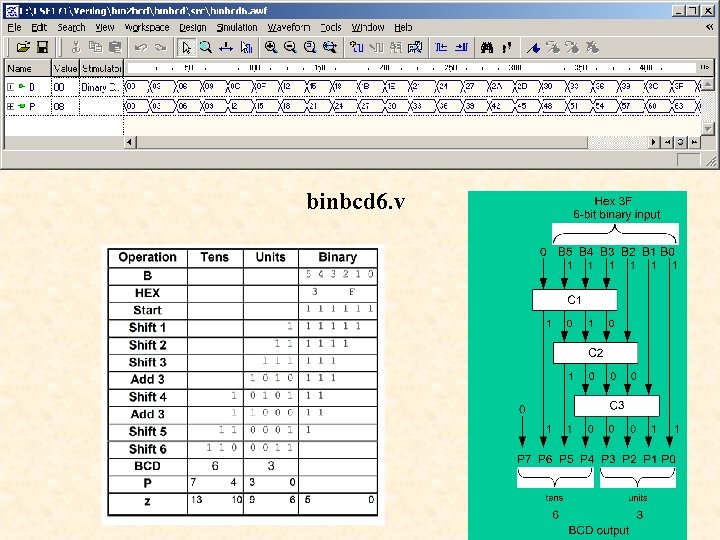
binbcd 6. v

module binbcd 8(B, P); input [7: 0] B; output [9: 0] P; binbcd 8. v reg [9: 0] P; reg [17: 0] z; integer i; always @(B) begin for(i = 0; i <= 17; i = i+1) z[i] = 0; z[10: 3] = B; for(i = 1; i <= 5; i = i+1) begin if(z[11: 8] > 4) z[11: 8] = z[11: 8] + 3; if(z[15: 12] > 4) z[15: 12] = z[15: 12] + 3; z[17: 1] = z[16: 0]; end P = z[17: 8]; endmodule

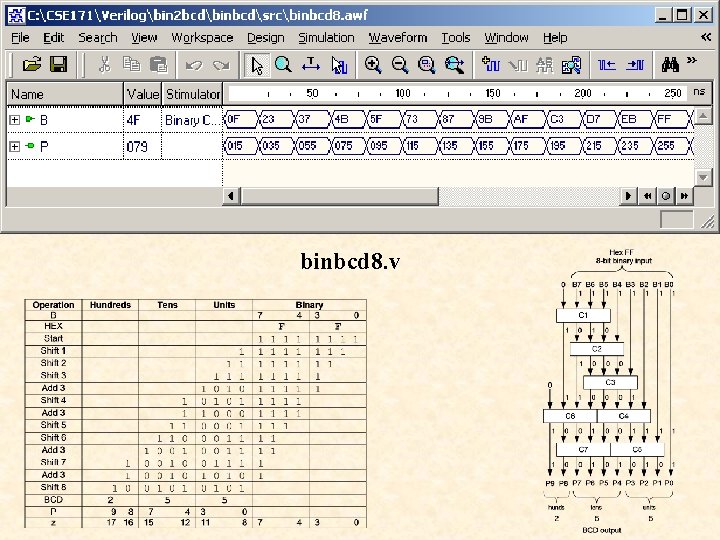
binbcd 8. v

module binbcd 9(B, P); input [8: 0] B; output [10: 0] P; binbcd 9. v reg [10: 0] P; reg [19: 0] z; integer i; always @(B) begin for(i = 0; i <= 19; i = i+1) z[i] = 0; z[11: 3] = B; for(i = 0; i <= 5; i = i+1) begin if(z[12: 9] > 4) z[12: 9] = z[12: 9] + 3; if(z[16: 13] > 4) z[16: 13] = z[16: 13] + 3; z[19: 1] = z[18: 0]; end P = z[19: 9]; endmodule

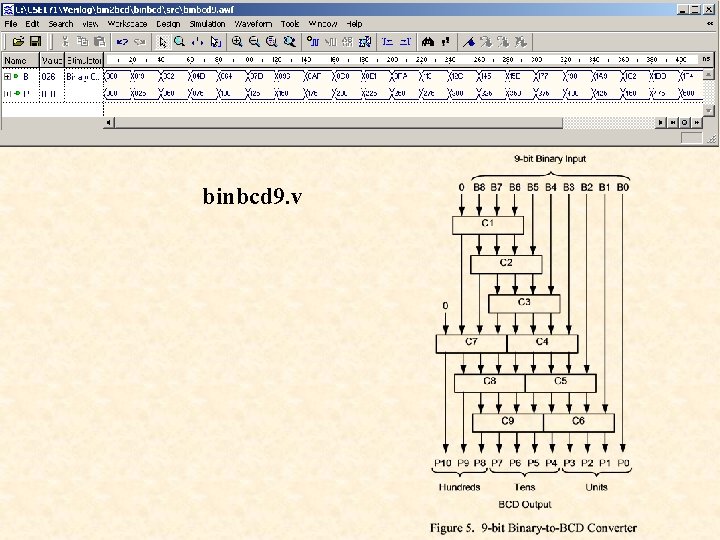
binbcd 9. v

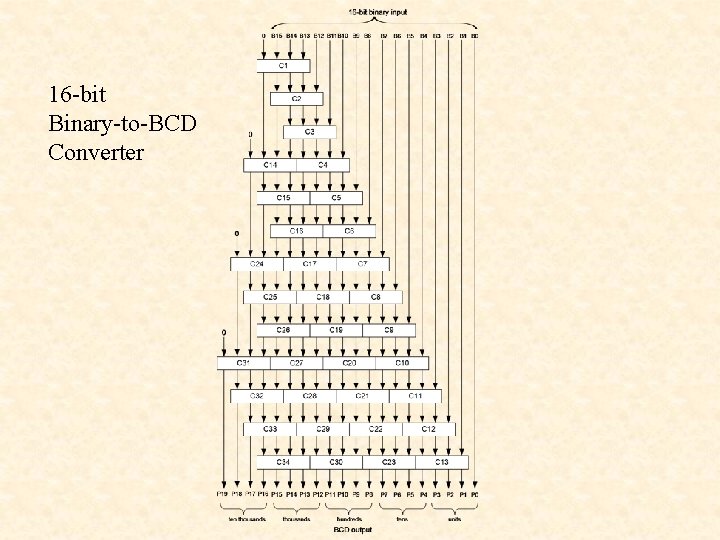
16 -bit Binary-to-BCD Converter

binbcd 16. v module binbcd 16(B, P); input [15: 0] B; output [18: 0] P; reg [31: 0] z; integer i;

always @(B) begin for(i = 0; i <= 31; i = i+1) z[i] = 0; z[18: 3] = B; for(i = 0; i <= 12; i = i+1) begin if(z[19: 16] > 4) z[19: 16] = z[19: 16] if(z[23: 20] > 4) z[23: 20] = z[23: 20] if(z[27: 24] > 4) z[27: 24] = z[27: 24] if(z[31: 28] > 4) z[31: 28] = z[31: 28] z[31: 1] = z[30: 0]; end P = z[31: 16]; endmodule + 3;

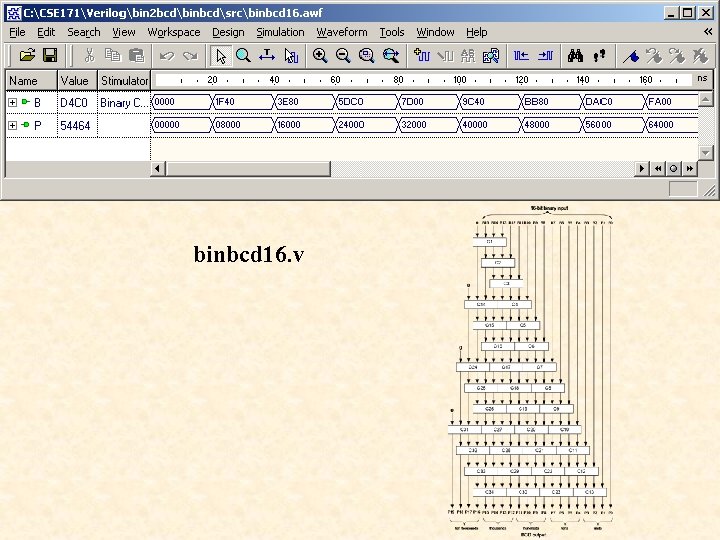
binbcd 16. v