Logic Circuits In todays lesson we will look

Logic Circuits • You might sometimes see diagrams that look like electrical circuits, but

Example Circuit AND • Symbols are combined and inputs labelled: • Output can be

NAND and NOR • With logic circuits, there are two new operators that you

Truth Table - NOR The NOR operator gives a false result if any of

Truth Table - NAND The NAND operator gives a false result if both of

Why Use NAND and NOR? • Remember De. Morgan’s Duals from last week? –

Simplification • Look at this circuit – it uses three components: • It represents

Another Example • What is the output of this logic circuit? A B C

Half-Adder • What is the output of this circuit? A B 0 0 0

Slides: 10

Download presentation

Logic Circuits In today’s lesson we will look at: • the symbols for NOT, AND, OR and EOR • using truth tables to represent logic circuits • two new operators – NAND and NOR • using equivalence to simplify circuits • the “half-adder” circuit

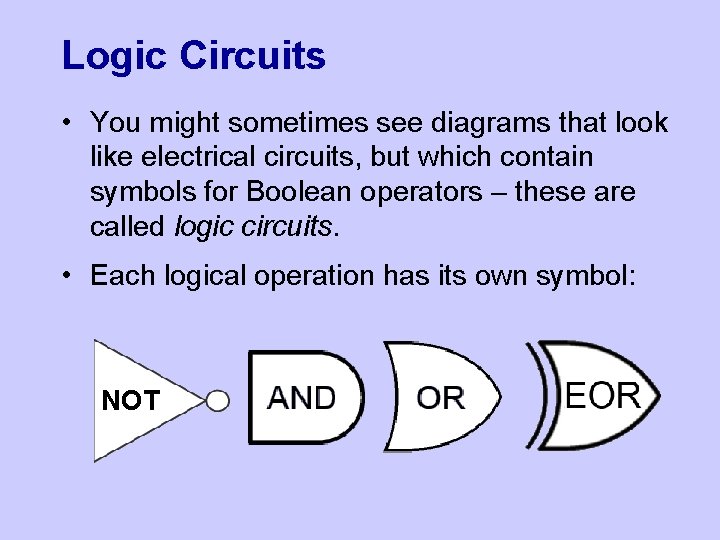
Logic Circuits • You might sometimes see diagrams that look like electrical circuits, but which contain symbols for Boolean operators – these are called logic circuits. • Each logical operation has its own symbol: NOT

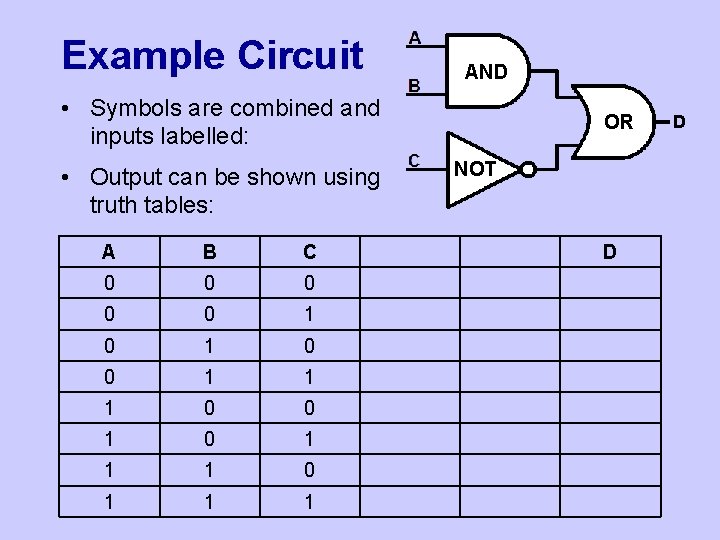
Example Circuit AND • Symbols are combined and inputs labelled: • Output can be shown using truth tables: A B C 0 0 0 1 1 1 0 0 1 1 1 OR NOT D D

NAND and NOR • With logic circuits, there are two new operators that you might come across – NAND and NOR: • Their names are short for NOT AND and NOT OR, which reminds us what they do. • NAND behaves like AND with a NOT after it, and NOR behaves like an OR with a NOT after it - i. e. the results are the opposite of a normal AND and OR.

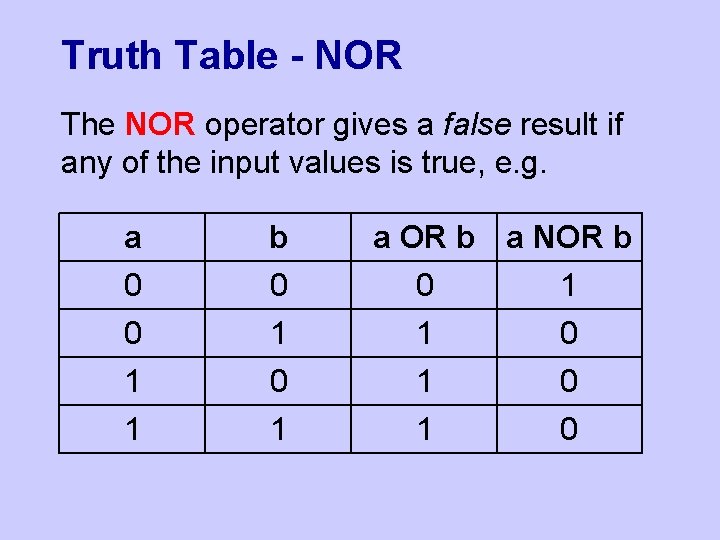
Truth Table - NOR The NOR operator gives a false result if any of the input values is true, e. g. a 0 b 0 a OR b a NOR b 0 1 1 0 1 0 1 1 1 0

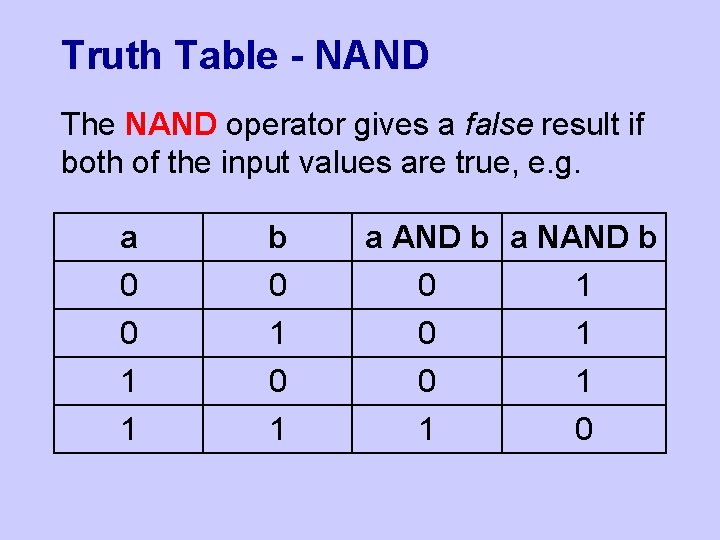
Truth Table - NAND The NAND operator gives a false result if both of the input values are true, e. g. a 0 b 0 a AND b a NAND b 0 1 0 1 1 0

Why Use NAND and NOR? • Remember De. Morgan’s Duals from last week? – NOT(a OR b) = NOT a AND NOT b – NOT(a AND b) = NOT a OR NOT b • The left-hand part of those equivalences are NOR and NAND, so they can be used to make logic circuits simpler. • Also, NAND is easy to manufacture because a single transistor behaves like a NAND gate, so circuits using NAND can be both logically and physically simpler and more efficient.

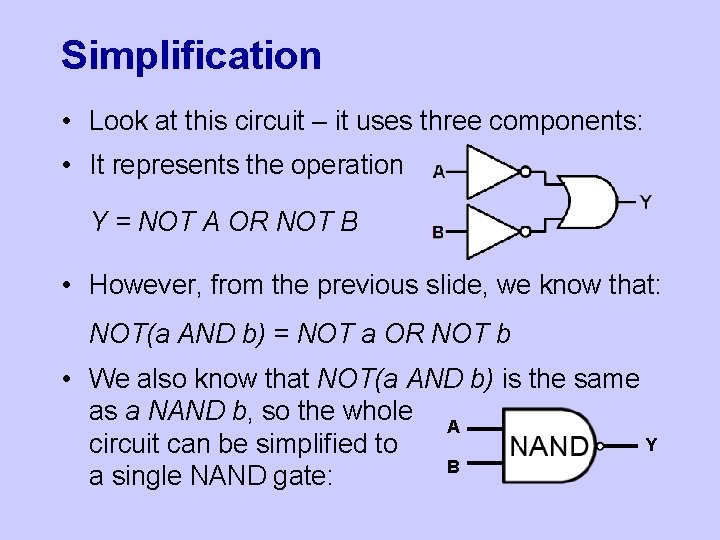
Simplification • Look at this circuit – it uses three components: • It represents the operation Y = NOT A OR NOT B • However, from the previous slide, we know that: NOT(a AND b) = NOT a OR NOT b • We also know that NOT(a AND b) is the same as a NAND b, so the whole A Y circuit can be simplified to B a single NAND gate:

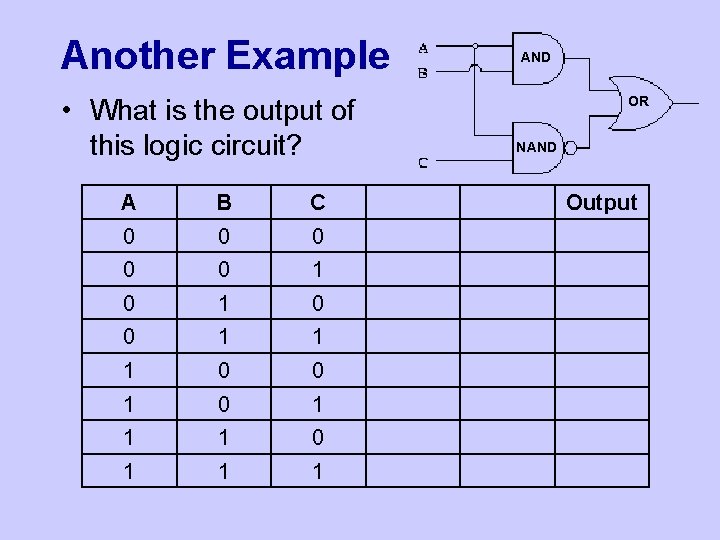
Another Example • What is the output of this logic circuit? A B C 0 0 0 1 1 1 0 0 1 1 1 AND OR NAND Output

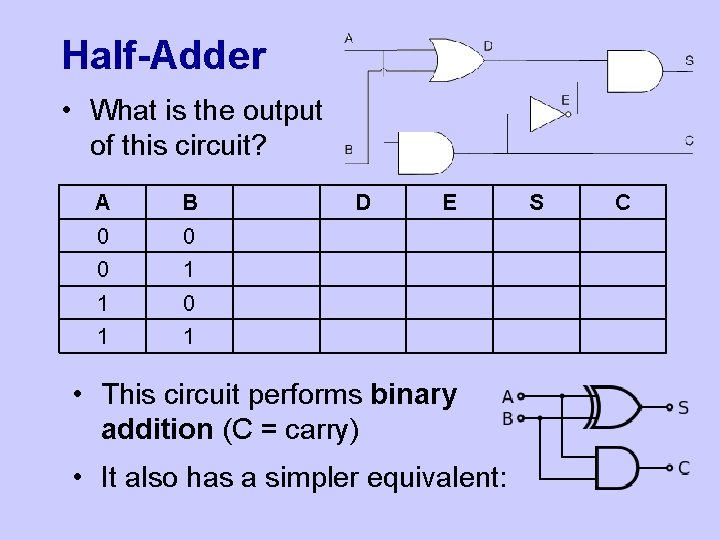
Half-Adder • What is the output of this circuit? A B 0 0 0 1 1 D E • This circuit performs binary addition (C = carry) • It also has a simpler equivalent: S C