Logic Circuits Design Chapter 1 Digital Systems and

Logic Circuits Design Chapter 1 Digital Systems and Information Mutah University Faculty of IT, Department of Software Engineering Dr. Ra’Fat A. AL-msie’deen

Course Info § Course title: Logic Circuits Design. § Credit hours (theory, practical): 3 hours. § Instructor: Dr. Ra’Fat A. AL-msie’Deen.

Required Textbook § Logic and Computer Design Fundamentals. – Fifth Edition. – M. Morris Mano, Charles R. Kime, Tom Martin. – 2014.

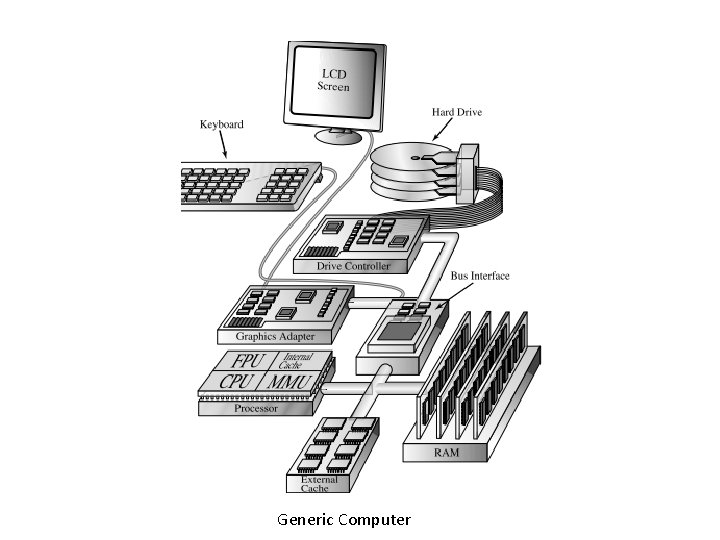
Generic Computer

Information Representation § Digital systems store, move, and process information. § Information represents a broad range of phenomena from: – The physical world: • Characterized by parameters such as weight, temperature, and frequency. • Most physical parameters are continuous: capable of taking on all possible values over a defined range. – Man-made world: • Such as business records using words, quantities, and currencies. • Parameters are discrete in nature. § In general, information systems must be able to represent both continuous and discrete information.

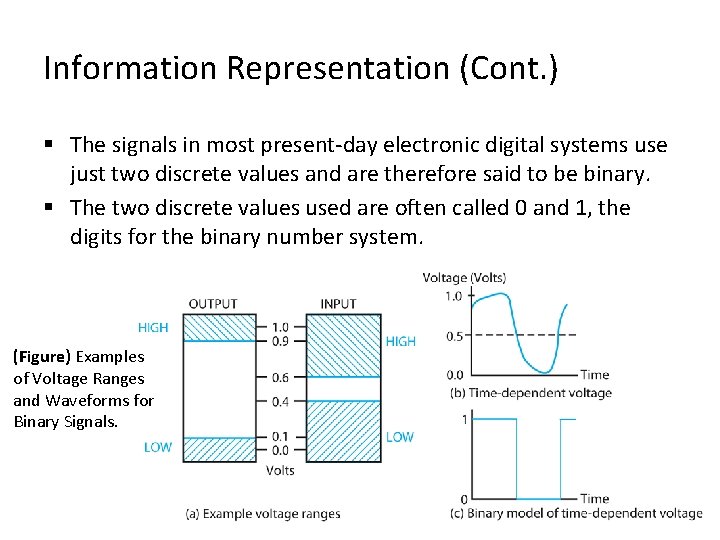
Information Representation (Cont. ) § The signals in most present-day electronic digital systems use just two discrete values and are therefore said to be binary. § The two discrete values used are often called 0 and 1, the digits for the binary number system. (Figure) Examples of Voltage Ranges and Waveforms for Binary Signals.

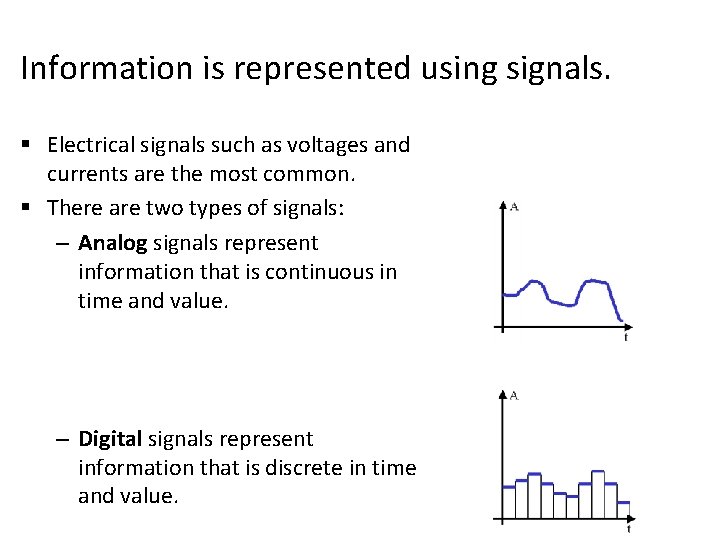
Information is represented using signals. § Electrical signals such as voltages and currents are the most common. § There are two types of signals: – Analog signals represent information that is continuous in time and value. – Digital signals represent information that is discrete in time and value.

What is a digital system? § It is a system that manipulates (processes) discrete elements of information. § A digital system is a discrete information processing system. § Examples of digital systems: – the calculator, – digital voltmeters, – and general purpose computers. § In such systems, all quantities are represented using two values. § Note: if the system in Not Digital, it is "Analog".

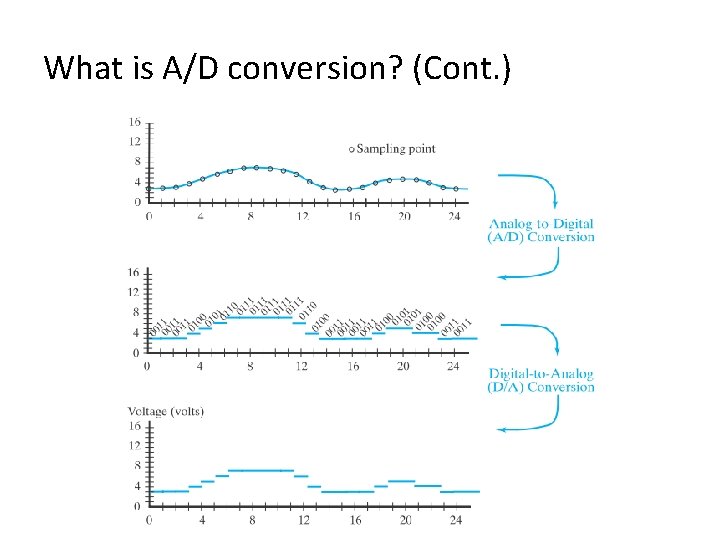
What is A/D conversion? §

What is A/D conversion? (Cont. )

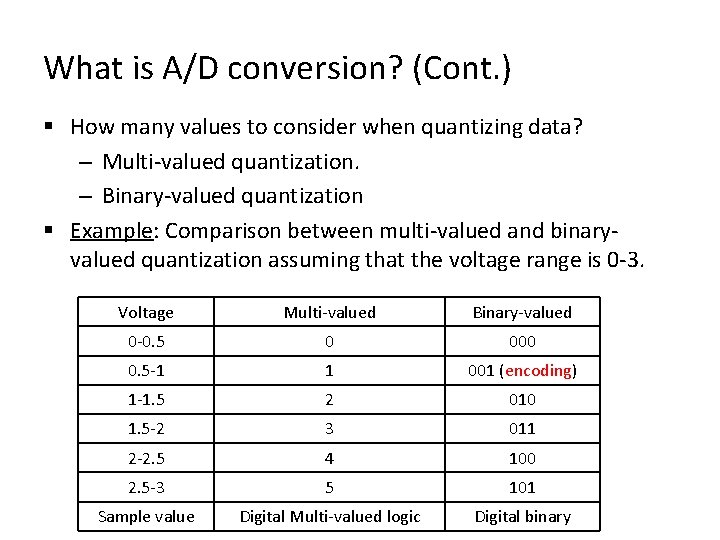
What is A/D conversion? (Cont. ) § How many values to consider when quantizing data? – Multi-valued quantization. – Binary-valued quantization § Example: Comparison between multi-valued and binaryvalued quantization assuming that the voltage range is 0 -3. Voltage Multi-valued Binary-valued 0 -0. 5 0 000 0. 5 -1 1 001 (encoding) 1 -1. 5 2 010 1. 5 -2 3 011 2 -2. 5 4 100 2. 5 -3 5 101 Sample value Digital Multi-valued logic Digital binary

What is A/D conversion? (Cont. ) § Note that in order to transfer data in case of multi-valued quantization, we need fewer wires. § In this example, the multi-valued quantized data requires one wire whereas binary-valued quantized data requires three wires. ü However, binary quantization is preferred over multivalued quantization since it provides higher immunity to noise. ü In general, binary systems are preferred since they are simpler, easy to design, and extremely reliable. ü Note: Always keep in mind that digital does not mean binary.

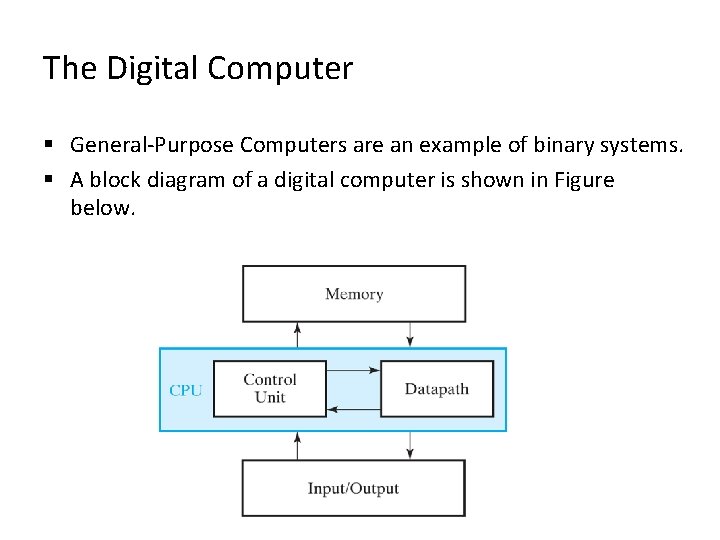
The Digital Computer § General-Purpose Computers are an example of binary systems. § A block diagram of a digital computer is shown in Figure below.

The Digital Computer § The memory stores programs as well as input, output, …. § The datapath (ALU) performs arithmetic and other dataprocessing operations as specified by the program. § The control unit supervises the flow of information between the various units. § A datapath, when combined with the control unit, forms a component referred to as a central processing unit, or CPU. § Input device: keyboard. § Output device: LCD (liquid crystal display). – These devices use digital logic circuits

Digital logic § Digital logic: is a science that deals with circuits that operate on a set of two-valued elements; binary values.

Digital logic (Cont. ) § Physical quantities: continuous. § Signal: mathematical function that describes physical quantities. § Digital signal: discrete in time and finite. § Analog signal: infinite values. § Again: why digital? – Analog has errors. – Digital systems have excellent noise immunity. § Most real life signals are analog signals (continuous)

Number Systems § Most Significant Digit (MSD) Least Significant Digit (LSD)

The Binary Numbering System § The binary number system is a base 2 system with two digits: 0 and 1. § A binary digit is called a bit. § bit - binary digit. § The decimal equivalent of a binary number can be found by expanding the number into a power series with a base of 2. – For example, – (11010)2 = 1 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = (26)10

The Binary Numbering System (Cont. ) § The digits in a binary number are called bits. § When a bit is equal to 0, it does not contribute to the sum during the conversion. § Therefore, the conversion to decimal can be obtained by adding the numbers with powers of two corresponding to the bits that are equal to 1. – For example, • (110101. 11)2 = ( ? )10 – Solution: • (110101. 11) 2 = 25 + 24 + 22 + 20 + 2 -1 + 2 -2 » = 32 + 16 + 4 + 1 + 0. 5 + 0. 25 » = (53. 75)10

Negative Exponents § The exponent of a number says how many times to use the number in a multiplication. – In this example: 82 = 8 × 8 = 64 § In words: 82 can be called "8 to the second power", "8 to the power 2" or simply "8 squared“. § But those are positive exponents, what about something like: 8 -2. – That exponent is negative. . . what does it mean? • Example: 8 -1 = 1 ÷ 81 = 1/8 = 0. 125. • Example: 2 -2 = 1 ÷ 22 = 1/4 = 0. 25. • Example: 2 -1 = 1 ÷ 21 = 1/2 = 0. 5.

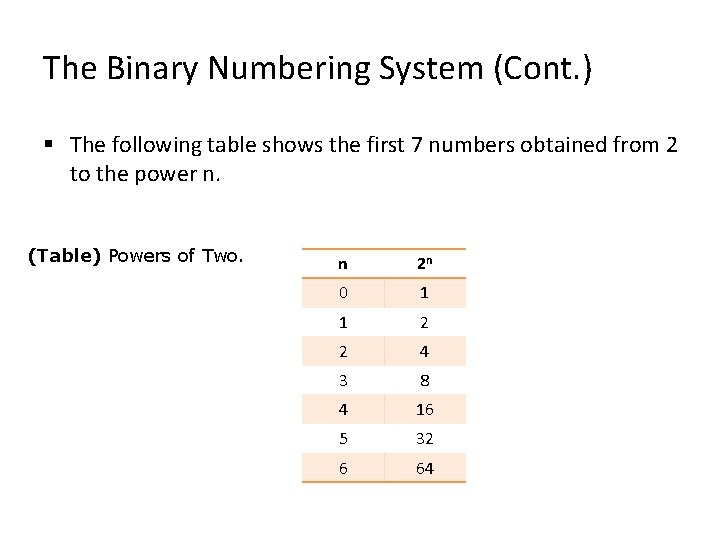
The Binary Numbering System (Cont. ) § The following table shows the first 7 numbers obtained from 2 to the power n. (Table) Powers of Two. n 2 n 0 1 1 2 2 4 3 8 4 16 5 32 6 64

The Octal Numbering System § r = 8 (23), allowed digits: {0, 1, 2, 3, …. . , 7}. – Example: • (127. 4)8 = ( ? )10 – Solution: • (127. 4)8 = 1*82 + 2*81 + 7*80 + 4*8 -1 » = (87. 5) 10 (Table) Powers of eight. n 8 n 0 1 1 8 2 64 3 512

The Hexadecimal Numbering System § (Table) Powers of 16. n 16 n 0 1 1 16 2 256 3 4096

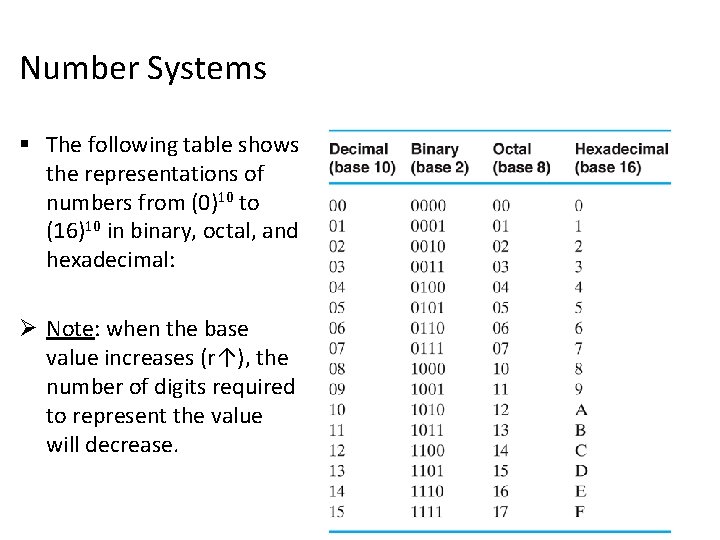
Number Systems § The following table shows the representations of numbers from (0)10 to (16)10 in binary, octal, and hexadecimal: Ø Note: when the base value increases (r↑), the number of digits required to represent the value will decrease.

Conversion between Numbering Systems §

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: • Use repeated integer divisions on successive quotients with base r and save the remainders until the quotient is 0. Then, read the remainders from the bottom to the top. – Example: (153)10 = (? )8 “Conversion of Decimal integers to Octal” – Solution: 153 1 19 3 2 2 Least significant digit Most significant digit 0 – Solution: (153)10 = (231)8 153 /8 = 19, remainder=1 19/8 = 2, remainder=3 2/8 = 0, remainder=2

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: – Conversion of Decimal integers to binary – Example: (73)10 = (? )2 73 1 36 0 18 0 9 1 4 0 2 0 1 1 0 – Solution: (73)10 = (1001001)2 Least significant digit (LSD) Most significant digit (MSD)

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: – Conversion of Decimal integers to Hexadecimal – Example: (245)10 = (? )16 245 5 Least significant digit (LSD) 15 15 Most significant digit (MSD) 0 – Solution: (245)10 = (F 5)16

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: – For the fractional part: • Use repeated multiplications with base r on the fractional part and save the integer parts. Stop when the fraction is 0. Then, read the integer parts from top to bottom. • Example: (0. 375)10 = (? )2 • Solution: 0. 375 *2 = 0. 75 Integer part = 0 0. 75 *2 = 1. 5 Integer part = 1 0. 5 *2 = 1. 0 Integer part = 1 • Solution: (0. 375)10 = (0. 011)2 Most significant digit Least significant digit

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: – For the fractional part: • Example: Convert (0. 513)10 to a three-digit octal fraction. • Note: The process of multiplying the fractions by r does not necessarily end with zero. In this case, the number of digits of the fraction to be used from the conversion must be specified. 0. 513 *8 = 4. 104 Integer part = 4 0. 104 *8 = 0. 832 Integer part = 0 0. 832 *8 = 6. 656 Integer part = 6 0. 656 *8 = 5. 248 Integer part = 5 Most significant digit Least significant digit • Solution: (0. 513)10 = (0. 4065)8 – The fourth digit (5) is used for rounding in base 8 of the second-tothe-last digit (6). • Solution: (0. 513)10 = (0. 407)8

Conversion between Numbering Systems (Cont. ) 2. Conversion from base 10 to any base (r): – For the integer part: – For the fractional part: • Example: (41. 6875)10 = (? )2 Fractional Part Integer Part 41 1 20 0. 6875 *2 = 1. 375 Integer part = 1 0 0. 375 *2 = 0. 75 Integer part = 0 10 0 0. 75 *2 = 1. 5 Integer part = 1 5 1 0. 5 *2 = 1. 0 Integer part = 1 2 0 1 1 0 Least significant digit Most significant digit MSD LSD Always check your result • Solution: (41. 6875)10 = (101001. 1011)2

Conversion between Numbering Systems (Cont. ) § 57 1 Least significant digit 28 0 14 0 7 1 3 1 1 1 Most significant digit 0

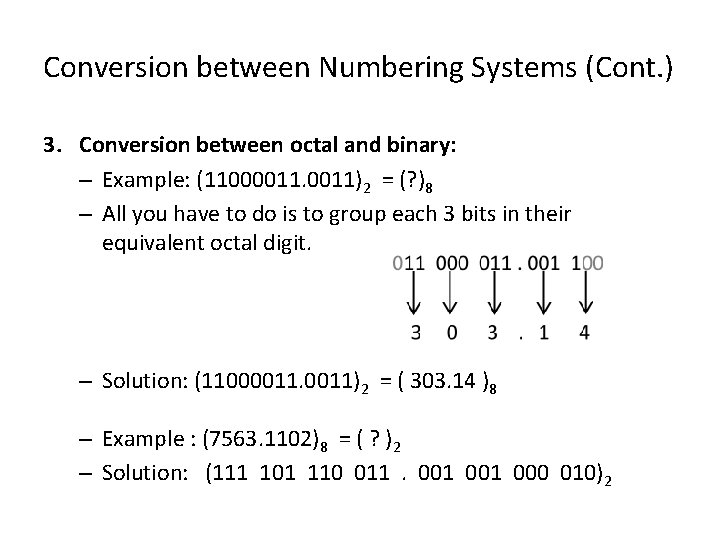
Conversion between Numbering Systems (Cont. ) 3. Conversion between octal and binary: – Example: (11000011)2 = (? )8 – All you have to do is to group each 3 bits in their equivalent octal digit. – Solution: (11000011)2 = ( 303. 14 )8 – Example : (7563. 1102)8 = ( ? )2 – Solution: (111 101 110 011. 001 000 010)2

Conversion between Numbering Systems (Cont. ) 4. Conversion between hexadecimal and binary: – In hexadecimal r = 16 = 24. – Hence each hexadecimal digit = 4 bits. • Example: (F 13. 67)16 = ( ? )2 • Solution: (1111 0001 0011. 0110 0111)2 • Example: (1101110001. 110111)2 = ( ? )16 • Solution: (371. DC)16

Conversion between Numbering Systems (Cont. ) 4. Conversion between hexadecimal and binary: – Example: (D 041. 32)16 = ( ? )8 – Solution: • (D 041. 32)16 = (1101 0000 0100 0001. 0011 0010)2 • (D 041. 32)16 = ( 150101. 144 )8 – Example: (365)r = (194)10; find r? – Solution: • 3 r 2 + 6 r + 5 = 194 • 3 r 2 + 6 r -189 = 0 • r 2 + 2 r – 63 = 0 • (r+9) (r-7) = 0 • So r = 7.

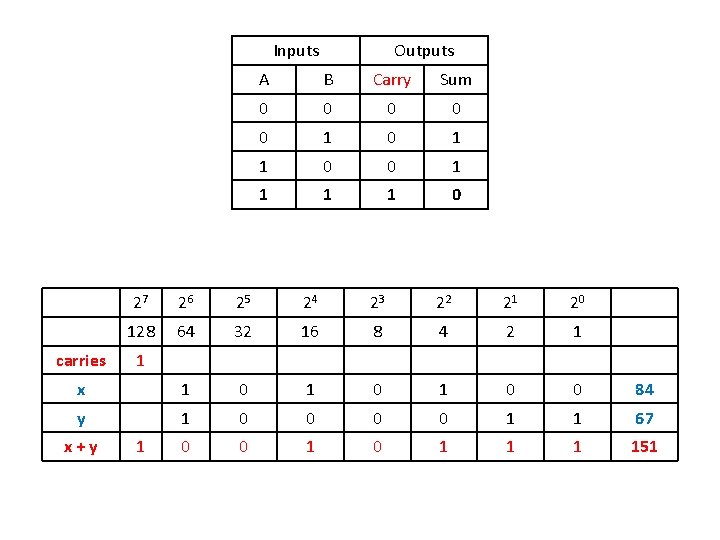
Arithmetic Operations § The sum of two binary numbers is calculated following the same rules as for decimal numbers, – Except that the sum digit in any position can be only 1 or 0. – Also, a carry in binary occurs if the sum in any bit position is greater than 1. • A carry in decimal occurs if the sum in any digit position is greater than 9. Inputs Outputs A B Carry Sum 0 0 0 1 1 0 • Examples of the addition of two binary numbers are as follows (note the names of the operands for addition):

Arithmetic Operations (Cont. ) § Example: Hexadecimal addition § Perform the addition (59 F)16 + (E 46)16

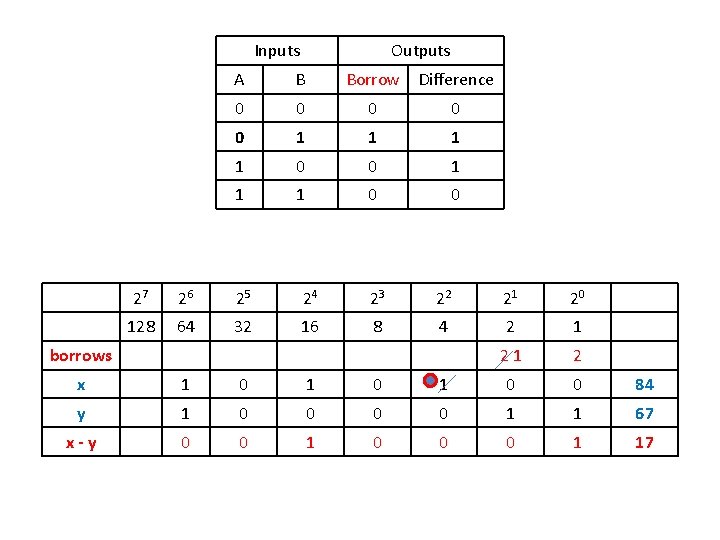
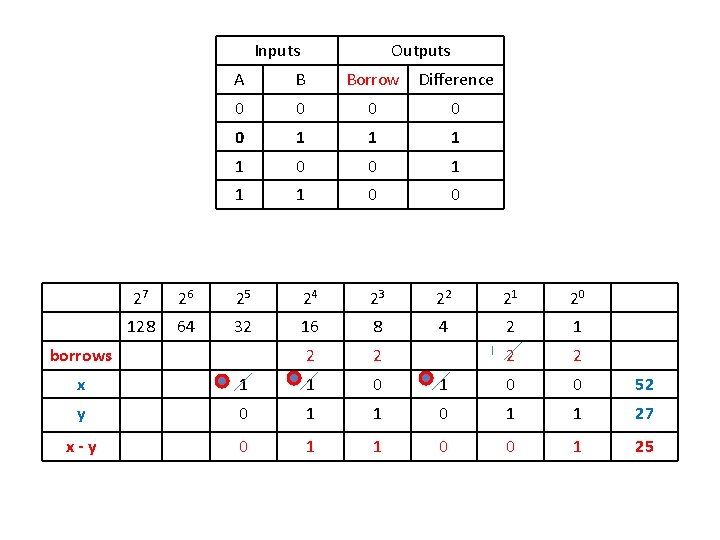
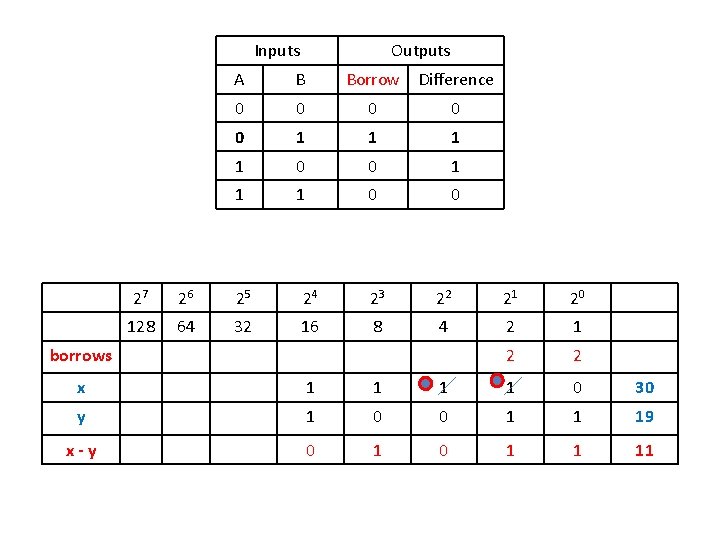
Arithmetic Operations (Cont. ) § The rules for subtraction are the same as in decimal, except that a borrow into a given column adds 2 to the minuend bit. Inputs Outputs A B Borrow Difference 0 0 0 1 1 1 0 0 § A borrow in the decimal system adds 10 to the minuend digit.

Arithmetic Operations (Cont. ) § The following are examples of the subtraction of two binary numbers; as with addition, note the names of the operands: § In the first example shown, no borrows occur, so the difference bits are simply the minuend bits minus the subtrahend bits. § In the second example, in the right position, the subtrahend bit is 1 with the minuend bit 0, so it is necessary to borrow from the second position as shown. This gives a difference bit in the first position of 1 (2 + 0 - 1 = 1). § In the second position, the borrow is subtracted, so a borrow is again necessary.

Arithmetic Operations (Cont. ) § Recall that, in the event that the subtrahend is larger than the minuend, we subtract the minuend from the subtrahend and give the result a minus sign. § This is the case in the third example, in which this interchange of the two operands is shown.

Subtraction Using 2 s Complement § Given the two binary numbers X = 1010100 and Y = 1000011, perform the subtraction X - Y and Y - X using 2 s complement operations. We have § X = 1010100 § 2 s complement of Y = 0111101 1 1 § Answer: X - Y = 0010001 27 X 1 0 1 0 0 Y 0 1 1 0 1 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 x 1 0 1 0 0 84 Discard end carry 27 y 1 0 0 1 1 67 Answer: X - Y = x-y 0 0 1 0 0 0 1 17 1 0 0 0 1

Subtraction Using 2 s Complement … § Given the two binary numbers X = 1010100 and Y = 1000011, perform the subtraction X - Y and Y - X using 2 s complement x 1 0 1 0 operations. We have 0 1 0 1 § Y = 1000011 + § 2 s complement of X = 0101100 2’s complement = § Sum = 1101111 0 1 1 0 § Answer: Y - X = - (2 s complement of 1101111) = - 0010001. 0 1 1 0 27 26 25 24 23 22 21 20 Y 1 0 0 1 1 128 64 32 16 8 4 2 1 X 0 1 1 0 0 x 1 0 1 0 0 84 y 1 0 0 1 1 67 y-x -0 0 1 0 0 0 1 17 1 1 0 1 1 There is no end carry. - 0 0 1 0 0 0 1

Subtraction Using 2 s Complement … § The subtraction of two n-digit unsigned numbers, M - N, in binary can be done as follows: 1. Add the 2 s complement of the subtrahend N to the minuend M. This performs M + (2 n - N) = M - N + 2 n. 2. If M >= N, the sum produces an end carry, 2 n. Discard the end carry, leaving result M - N. 3. If M < N, the sum does not produce an end carry, since it is equal to 2 n - (N - M), the 2 s complement of N - M. Perform a correction, taking the 2 s complement of the sum and placing a minus sign in front to obtain the result - (N M).

Arithmetic Operations (Cont. ) § 1 1 1 X 1 0 1 0 0 Y 0 1 1 0 0 0 1 Discard end carry 27 Answer: X - Y = 0 0 1 0 0 0 1 x 1 0 1 0 0 0 1 0 1 1 + 1 2’s complement = 0 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 x 1 0 1 0 0 84 y 1 0 0 1 1 67 1 0 1 1 0 0 Y 1 0 0 1 1 X 0 1 1 0 0 1 1 1 1 There is no end carry. - 0 0 1 0 0 0 1

Inputs Outputs A B Carry Sum 0 0 0 1 1 0 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 x 1 0 1 0 0 84 y 1 0 0 1 1 67 0 0 1 1 1 151 carries x+y 1 1

Inputs Outputs A B Borrow Difference 0 0 0 1 1 1 0 0 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 21 2 borrows x 1 0 1 0 0 84 y 1 0 0 1 1 67 x-y 0 0 1 0 0 0 1 17

Inputs Outputs A B Borrow Difference 0 0 0 1 1 1 0 0 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 2 2 borrows x 1 1 0 0 52 y 0 1 1 27 x-y 0 1 1 0 0 1 25

Inputs Outputs A B Borrow Difference 0 0 0 1 1 1 0 0 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 2 2 borrows x 1 1 0 30 y 1 0 0 1 1 19 x-y 0 1 1 11

Arithmetic Operations (Cont. ) § The final operation to be illustrated is binary multiplication, which is quite simple. § The multiplier digits are always 1 or 0. § Therefore, the partial products are equal either to the multiplicand or to 0. § Multiplication is illustrated by the following example:

Binary Codes §

Binary Codes (Cont. ) §

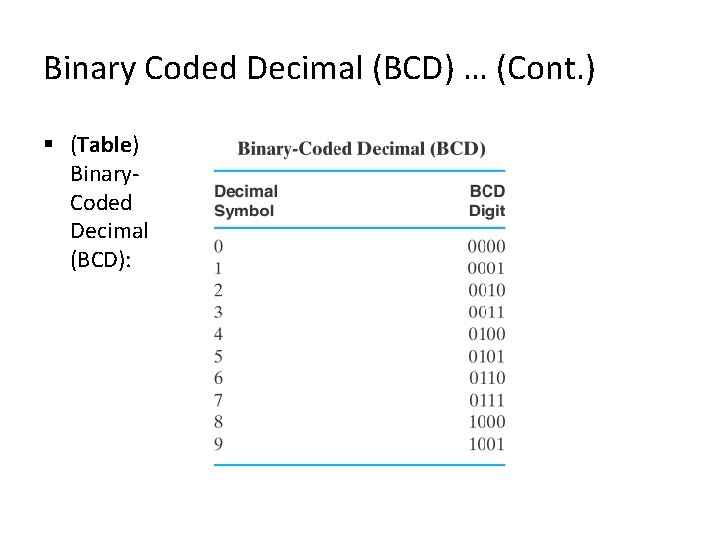
Binary Coded Decimal (BCD) §

Binary Coded Decimal (BCD) … (Cont. ) § (Table) Binary. Coded Decimal (BCD):

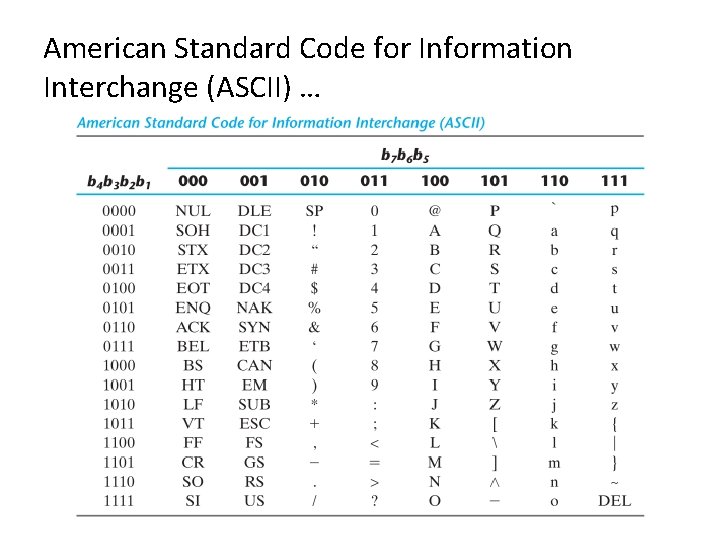
American Standard Code for Information Interchange (ASCII) §

American Standard Code for Information Interchange (ASCII) …

Unicode §

Gray Code § Non-numeric code. § There is only one bit change between adjacent codes. § For example, in order to encode the colors (red, yellow, blue, green) using gray codes, the codes will be assigned to the colors as follows: – Red: 00 – Yellow: 01 – Blue: 11 – Green: 10 § The following table shows the binary code and gray code as we count from 000 to 111 and the number of bits changing between adjacent codes for each code.

Parity Code § Non-numeric code. § Extra bit(s) added to the original data to aid error detection. § In case of a single parity bit, an additional bit is added make the total number of 1 s in the resulting code either even or odd. § The following table shows an example of forming even and odd parity. In each case, the extra parity bit is added in the most significant position of the code.

Parity Code (Cont. ) § The parity bit is helpful in detecting errors during transmission of information from one location to another. § For example, assume even parity is used, the following steps are performed between two end points that uses parity to perform error detection: – Even parity is generated at the sending end. – Data is transmitted. – Parity is checked at the destination. If it is odd, then the system detects that at least one bit has changed. § Such a system detects one, three, …. . odd number of errors. § In order to detect errors more efficiently, more parity bits are needed.

Logic Circuits Design Chapter 1 Digital Systems and Information Mutah University Faculty of IT, Department of Software Engineering Dr. Ra’Fat A. AL-msie’deen