Logic and Reasoning The philosophers toolbox Why does

Logic and Reasoning The philosopher’s toolbox

Why does logic matter? As a class, come up with some ways in which we use logic every day. (5 -10 minute brainstorm)

How do we use logic Make decisions Win arguments Assess truth Explore the dangers of dihydrogen monoxide at www. dhmo. org

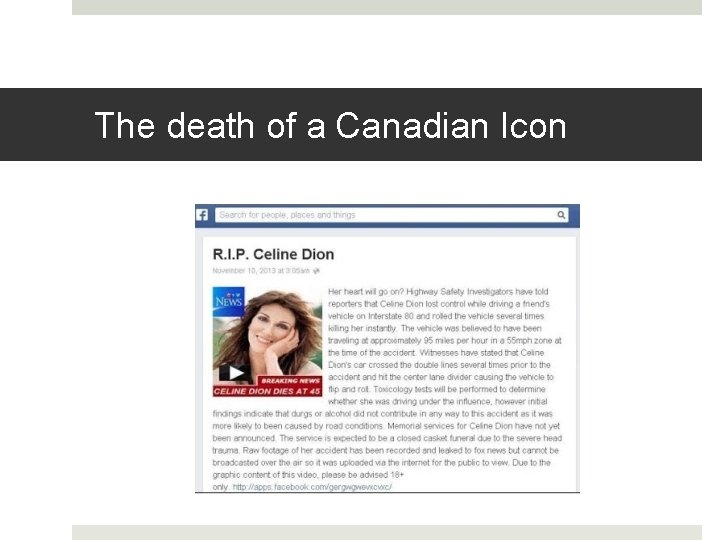
The death of a Canadian Icon

Logic - definition From Greek word logos (speech or reason) Logike tekhne is _____________ Area of philosophy that studies correct _____ and sound judgement Helps to __________________________. Exposes faulty arguments by examining assumptions about what is true. Not concerned with ______ of views (conservative vs. liberal, generous vs. stingy). Only concerned with what can and cannot be justified.

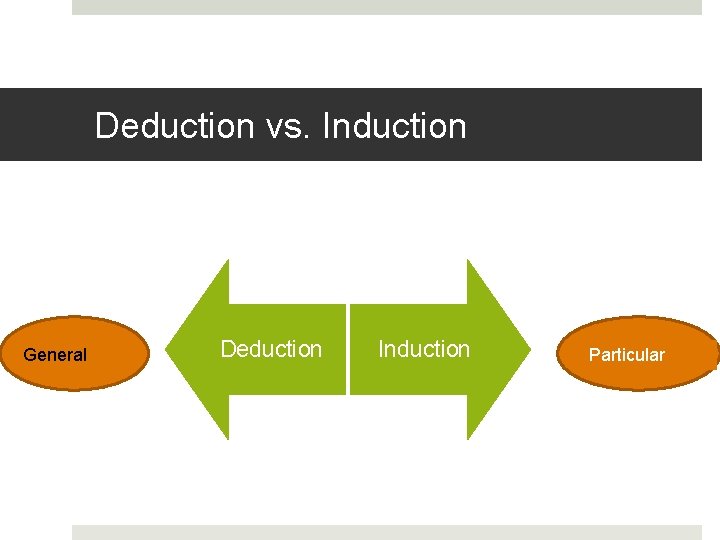
Deduction vs. Induction General Deduction Induction Particular

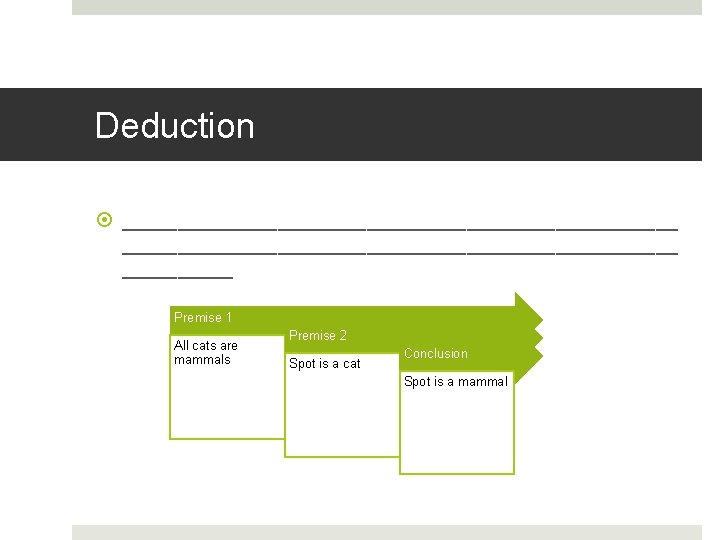
Deduction __________________________________________________ Premise 1 All cats are mammals Premise 2 Spot is a cat Conclusion Spot is a mammal

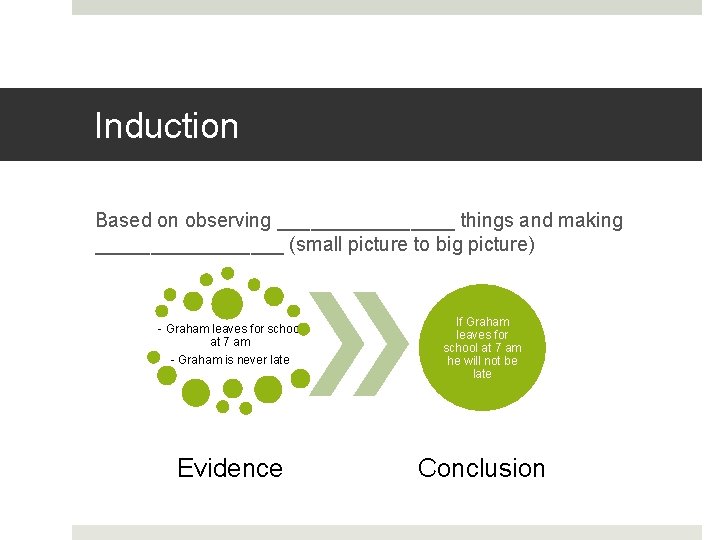
Induction Based on observing ________ things and making _________ (small picture to big picture) - Graham leaves for school at 7 am - Graham is never late If Graham leaves for school at 7 am he will not be late Evidence Conclusion

Three laws of thought Aristotle Organon Foundations of formal logic and deductive reasoning a) b) c) ______________________________

Law of Non contradiction Something cannot be said to both be and not to be at the same time. Example: If we conclude that the apple is the colour red, it cannot be said to be ‘not red’ at the same time

Law of the Excluded middle Something must either be or not be. Example: Either Nikita exists or does not exist. There is no third possibility or middle

Law of Identity Something is what it says it is Example: Carolina is Carolina, Bhavik is Bhavik cannot be Carolina

Ship of Theseus

Beyond Aristotle 12 th century French monk Peter Abelard compiled 158 contradictory viewpoints on philosophical/theological questions in Sic et Non 17 th century, Francis Bacon and scientific method sees shift to inductive reasoning 19 th century mathematician George Boole uses chains of deductiive reasoning in algebra Kurt Godel, mathematician proved that some mathematical statements cannot be proven even if correct rules and principles are applied

Terms Argument – __________ consisting of premise(s) and a conclusion Premise – factual statement or ________. Provide reasons for believing a conclusion Syllogism – basic form of argument that uses ________ reasoning. A syllogism consists of at least two premises and a conclusion

Syllogism All humans are mortal Aristotle is a human Therefore Aristotle is mortal

Write your own syllogism Use any of the following words to create a syllogism of your own Apples Baking Cars Dancehall reggae Entropy Fallacy Gophers Helicopter Ice cream

Truth and Validity Truth- refers to the truth of content within a statement or premise Validity – refers to the correctness of reasoning Logicians are more concerned with validity than the truth of an argument’s statements

Valid but untrue Premise: all humans are immortal Premise: I am human Conclusion: Therefore I am immortal Are these true? Are these valid? Premise is untrue but arguments are still valid because the conclusions follows logically from the premises

Validity, Soundness and Reliability In deductive arguments, the truth of the premises guarantees the truth of the conclusion. An argument is said to be sound if its form is valid and its premises are true. The same test cannot be applied to inductive arguments which are identified as “reliable” or “unreliable”