Logic and Computer Design Fundamentals Boolean Algebra and

Binary Logic and Gates § Binary variables take on one of two values. § Logical operators operate on binary values and binary variables. § Basic logical operators are the logic functions AND, OR and NOT. § Logic gates implement logic functions. § Boolean Algebra: a useful mathematical system for specifying and transforming logic functions. § We study Boolean algebra as a foundation for designing and analyzing digital systems! 2

Binary Variables § Recall that the two binary values have different names: • • True/False On/Off Yes/No 1/0 § We use 1 and 0 to denote the two values. § Variable identifier examples: • A, B, y, z, or X 1 for now • RESET, START_IT, or ADD 1 later 3

Logical Operations § The three basic logical operations are: • AND • OR • NOT § AND is denoted by a dot (·). § OR is denoted by a plus (+). § NOT is denoted by an overbar ( ¯ ), a single quote mark (') after, or (~) before the variable. 4

Notation Examples § Examples: • Y = A × B is read “Y is equal to A AND B. ” • z = x + y is read “z is equal to x OR y. ” • X = A is read “X is equal to NOT A. ” § Note: The statement: 1 + 1 = 2 (read “one plus one equals two”) is not the same as 1 + 1 = 1 (read “ 1 or 1 equals 1”). 5

Operator Definitions § Operations are defined on the values "0" and "1" for each operator: AND 0· 0=0 0· 1=0 1· 0=0 1· 1=1 OR NOT 0+0=0 0+1=1 1+0=1 1+1=1 0=1 1=0 6

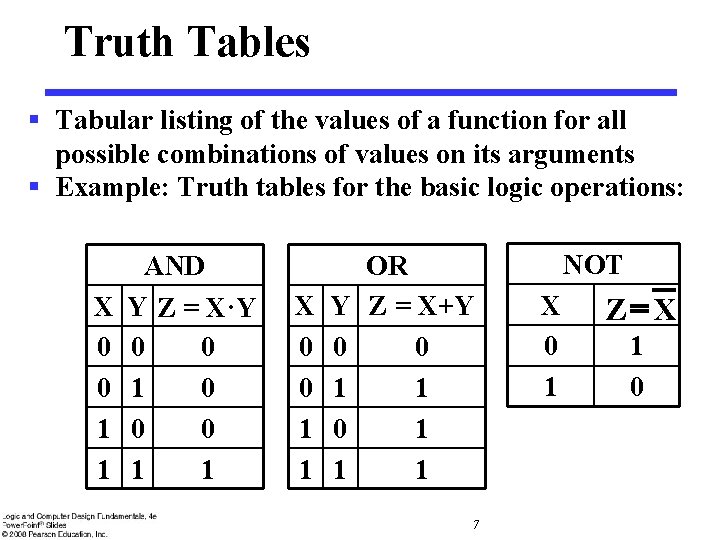
Truth Tables § Tabular listing of the values of a function for all possible combinations of values on its arguments § Example: Truth tables for the basic logic operations: X 0 0 1 1 AND Y Z = X·Y 0 0 1 0 0 0 1 1 X 0 0 1 1 Y 0 1 OR Z = X+Y 0 1 1 1 7 NOT X 0 1 Z=X 1 0

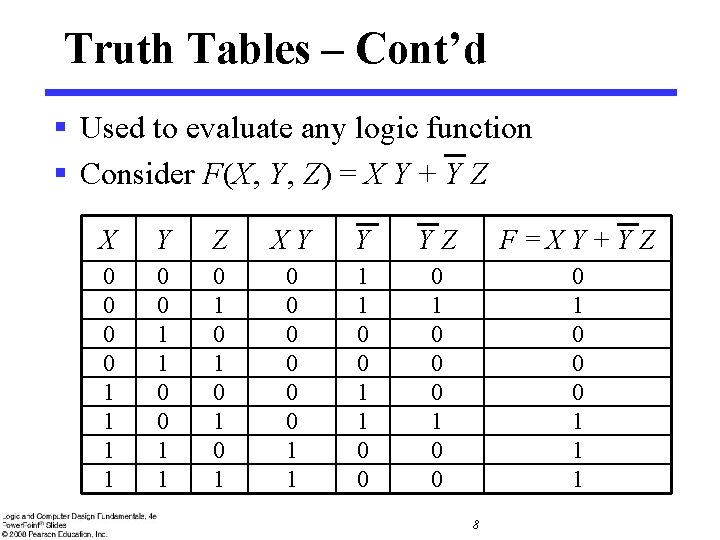
Truth Tables – Cont’d § Used to evaluate any logic function § Consider F(X, Y, Z) = X Y + Y Z XY Y YZ F=XY+YZ 0 0 1 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 1 8

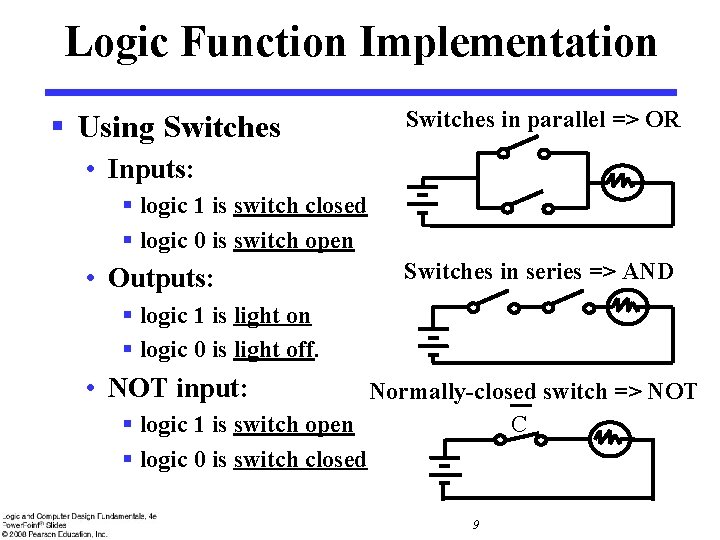
Logic Function Implementation § Using Switches in parallel => OR • Inputs: § logic 1 is switch closed § logic 0 is switch open • Outputs: Switches in series => AND § logic 1 is light on § logic 0 is light off. • NOT input: Normally-closed switch => NOT C § logic 1 is switch open § logic 0 is switch closed 9

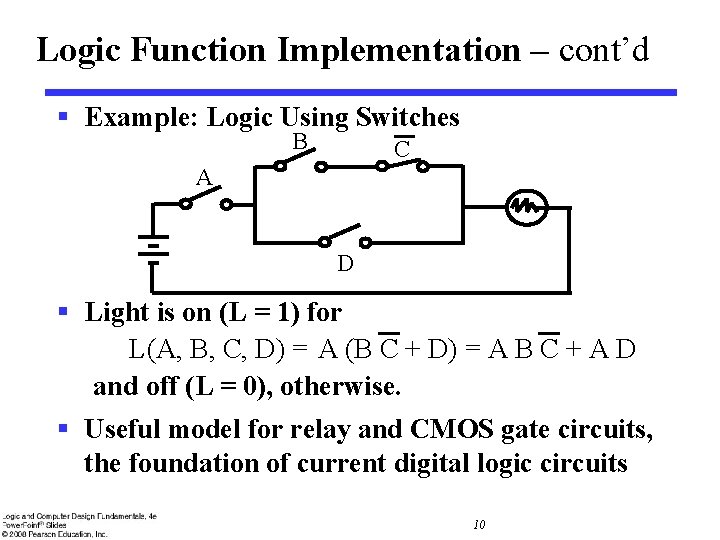
Logic Function Implementation – cont’d § Example: Logic Using Switches B C A D § Light is on (L = 1) for L(A, B, C, D) = A (B C + D) = A B C + A D and off (L = 0), otherwise. § Useful model for relay and CMOS gate circuits, the foundation of current digital logic circuits 10

Logic Gates § In the earliest computers, switches were opened and closed by magnetic fields produced by energizing coils in relays. The switches in turn opened and closed the current paths. § Later, vacuum tubes that open and close current paths electronically replaced relays. § Today, transistors are used as electronic switches that open and close current paths. 11

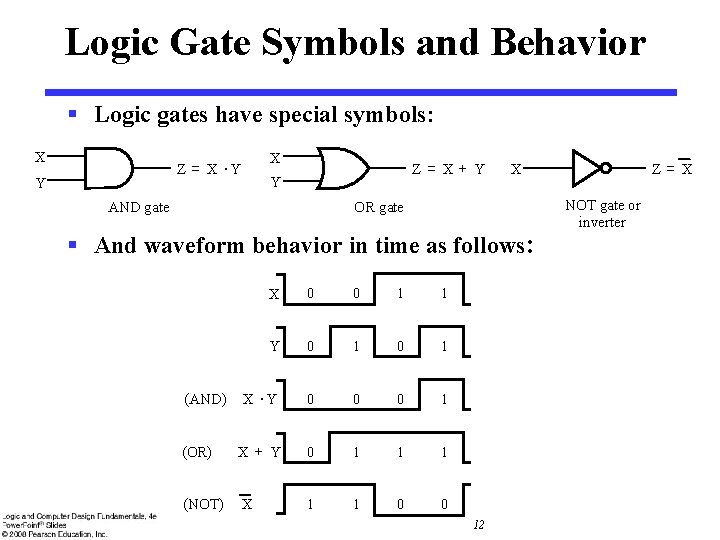
Logic Gate Symbols and Behavior § Logic gates have special symbols: X X Z = X ·Y Y Z= X+ Y Y X OR gate AND gate § And waveform behavior in time as follows: X 0 0 1 1 Y 0 1 X ·Y 0 0 0 1 (OR) X+ Y 0 1 1 1 (NOT) X 1 1 0 0 (AND) 12 Z= X NOT gate or inverter

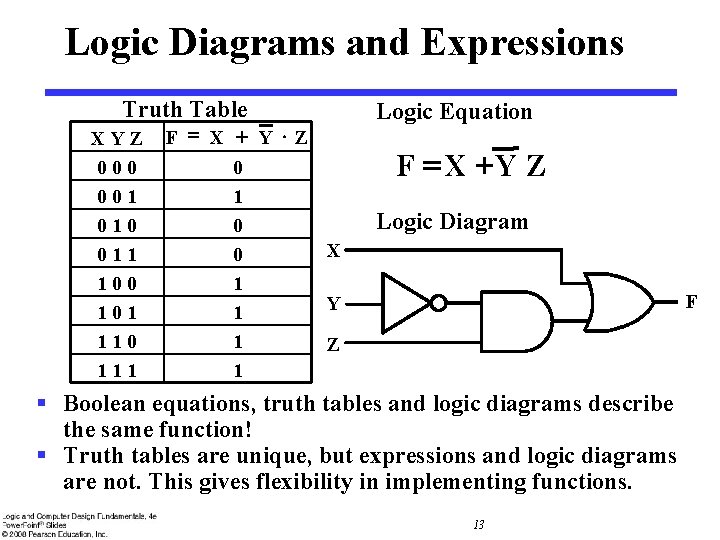
Logic Diagrams and Expressions Truth Table XYZ 000 001 010 011 100 101 110 111 F = X + Y ×Z 0 1 0 X 0 1 Y 1 1 Z 1 Logic Equation F = X +Y Z Logic Diagram F § Boolean equations, truth tables and logic diagrams describe the same function! § Truth tables are unique, but expressions and logic diagrams are not. This gives flexibility in implementing functions. 13

Gate Delay § In actual physical gates, if an input changes that causes the output to change, the output change does not occur instantaneously. § The delay between an input change and the output change is the gate delay denoted by t. G: 1 Input 0 1 Output 0 0 t. G 0. 5 1 t. G = 0. 3 ns Time (ns) 1. 5 14

Boolean Algebra § § 1. 3. 5. 7. 9. Invented by George Boole in 1854 An algebraic structure defined by a set B = {0, 1}, together with two binary operators (+ and ·) and a unary operator ( ) X+0= X X+1 =1 X+X =X X+X =1 2. 4. 6. 8. Identity element X. 1 =X X. 0 =0 X. X = X Idempotence X. X = 0 Complement X=X 10. X + Y = Y + X 12. (X + Y) + Z = X + (Y + Z) 14. X(Y + Z) = XY + XZ 16. X + Y = X. Y Involution 11. XY = YX Commutative Associative 13. (XY) Z = X(YZ) 15. X + YZ = (X + Y) (X + Z) Distributive De. Morgan’s 17. X. Y = X + Y 15

Some Properties of Boolean Algebra § Boolean Algebra is defined in general by a set B that can have more than two values § A two-valued Boolean algebra is also know as Switching Algebra. The Boolean set B is restricted to 0 and 1. Switching circuits can be represented by this algebra. § The dual of an algebraic expression is obtained by interchanging + and · and interchanging 0’s and 1’s. § The identities appear in dual pairs. When there is only one identity on a line the identity is self-dual, i. e. , the dual expression = the original expression. § Sometimes, the dot symbol ‘ ’ (AND operator) is not written when the meaning is clear 16

Dual of a Boolean Expression § Example: F = (A + C) · B + 0 dual F = (A · C + B) · 1 = A · C + B § Example: G = X · Y + (W + Z) dual G = (X+Y) · (W · Z) = (X+Y) · (W+Z) § Example: H = A · B + A · C + B · C dual H = (A+B) · (A+C) · (B+C) § Unless it happens to be self-dual, the dual of an expression does not equal the expression itself § Are any of these functions self-dual? H is self-dual (A+B)(A+C)(B+C)=(A+BC)(B+C)=AB+AC+BC 17

Boolean Operator Precedence § The order of evaluation is: 1. Parentheses 2. NOT 3. AND 4. OR § Consequence: Parentheses appear around OR expressions § Example: F = A(B + C)(C + D) 18

Boolean Algebraic Proof – Example 1 § A+A·B=A (Absorption Theorem) Proof Steps Justification A+A·B =A· 1+A·B Identity element: A · 1 = A · ( 1 + B) Distributive =A· 1 1+B=1 = A Identity element § Our primary reason for doing proofs is to learn: • Careful and efficient use of the identities and theorems of Boolean algebra, and • How to choose the appropriate identity or theorem to apply to make forward progress, irrespective of the application. 19

Boolean Algebraic Proof – Example 2 § AB + AC + BC = AB + AC (Consensus Theorem) Proof Steps Justification = AB + AC + BC = AB + AC + 1 · BC Identity element = AB + AC + (A + A) · BC Complement = AB + AC + ABC Distributive = AB + ABC + ACB Commutative = AB · 1 + ABC + AC · 1 + ACB Identity element = AB (1+C) + AC (1 + B) Distributive = AB. 1 + AC. 1 1+X = 1 = AB + AC Identity element 20

Useful Theorems § Minimization XY+XY=Y § Minimization (dual) (X+Y) = Y § Absorption X+XY=X § Absorption (dual) X · (X + Y) = X § Simplification X+XY=X+Y § Simplification (dual) X · (X + Y) = X · Y § De. Morgan’s § X+Y=X·Y § De. Morgan’s (dual) § X·Y=X+Y 21

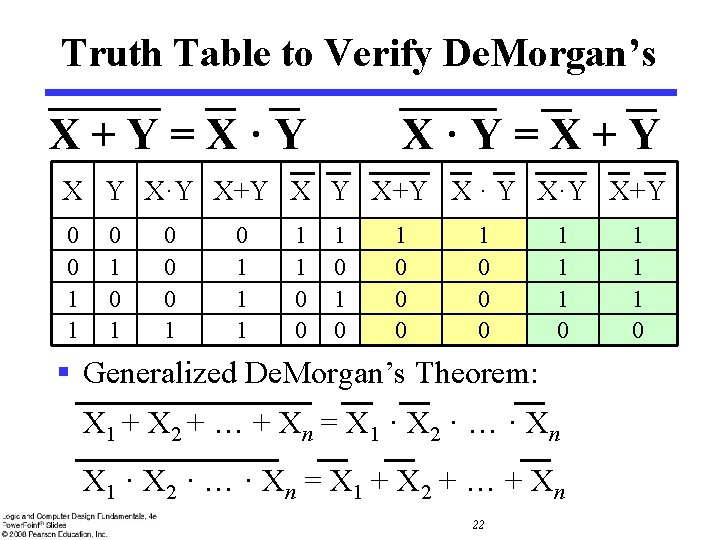
Truth Table to Verify De. Morgan’s X+Y=X·Y X·Y=X+Y X Y X·Y X+Y X · Y X·Y X+Y 0 0 1 1 0 1 0 0 0 1 1 1 0 0 1 0 1 0 0 0 1 1 1 0 § Generalized De. Morgan’s Theorem: X 1 + X 2 + … + Xn = X 1 · X 2 · … · Xn = X 1 + X 2 + … + Xn 22 1 1 1 0

Complementing Functions § Use De. Morgan's Theorem: 1. Interchange AND and OR operators 2. Complement each constant and literal § Example: Complement F = xy z + x y z F = (x + y + z) § Example: Complement G = (a + bc)d + e G = (a (b + c) + d) e 23

Expression Simplification § An application of Boolean algebra § Simplify to contain the smallest number of literals (variables that may or may not be complemented) A B + ACD + A BD + AC D + A BCD = AB + ABCD + A C D + A B D = AB + AB(CD) + A C (D + D) + A B D = AB + A C + A B D = B(A + AD) +AC = B (A + D) + A C (has only 5 literals) 24

Next … Canonical Forms § Minterms and Maxterms § Sum-of-Minterm (SOM) Canonical Form § Product-of-Maxterm (POM) Canonical Form § Representation of Complements of Functions § Conversions between Representations 25

Minterms § Minterms are AND terms with every variable present in either true or complemented form. § Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x), there are 2 n minterms for n variables. § Example: Two variables (X and Y) produce 2 x 2 = 4 combinations: XY (both normal) X Y (X normal, Y complemented) XY (X complemented, Y normal) X Y (both complemented) § Thus there are four minterms of two variables. 26

Maxterms § Maxterms are OR terms with every variable in true or complemented form. § Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x), there are 2 n maxterms for n variables. § Example: Two variables (X and Y) produce 2 x 2 = 4 combinations: X + Y (both normal) X + Y (x normal, y complemented) X + Y (x complemented, y normal) X + Y (both complemented) 27

Minterms & Maxterms for 2 variables § Two variable minterms and maxterms. x y Index Minterm Maxterm 0 0 0 m 0 = x y M 0 = x + y 0 1 1 m 1 = x y M 1 = x + y 1 0 2 m 2 = x y M 2 = x + y 1 1 3 m 3 = x y M 3 = x + y § The minterm mi should evaluate to 1 for each combination of x and y. § The maxterm is the complement of the minterm 28

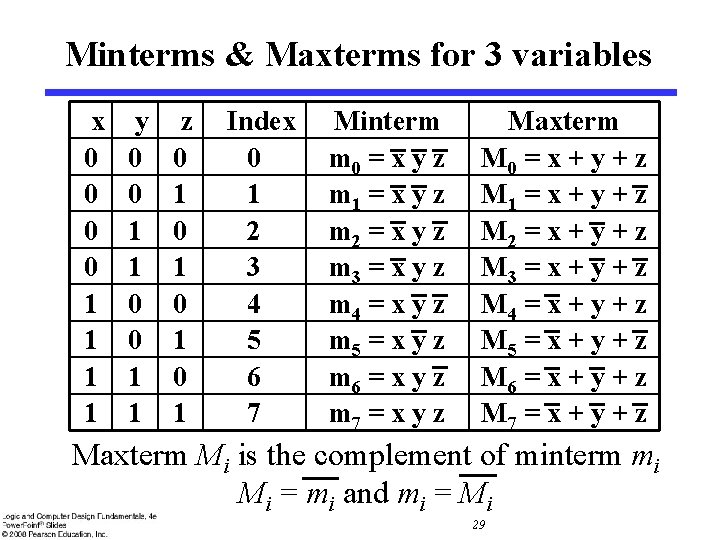
Minterms & Maxterms for 3 variables x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 Index 0 1 2 3 4 5 6 7 Minterm m 0 = x y z m 1 = x y z m 2 = x y z m 3 = x y z m 4 = x y z m 5 = x y z m 6 = x y z m 7 = x y z Maxterm M 0 = x + y + z M 1 = x + y + z M 2 = x + y + z M 3 = x + y + z M 4 = x + y + z M 5 = x + y + z M 6 = x + y + z M 7 = x + y + z Maxterm Mi is the complement of minterm mi Mi = mi and mi = Mi 29

Purpose of the Index § Minterms and Maxterms are designated with an index § The index number corresponds to a binary pattern § The index for the minterm or maxterm, expressed as a binary number, is used to determine whether the variable is shown in the true or complemented form § For Minterms: • ‘ 1’ means the variable is “Not Complemented” and • ‘ 0’ means the variable is “Complemented”. § For Maxterms: • ‘ 0’ means the variable is “Not Complemented” and • ‘ 1’ means the variable is “Complemented”. 30

Standard Order § All variables should be present in a minterm or maxterm and should be listed in the same order (usually alphabetically) § Example: For variables a, b, c: • Maxterms (a + b + c), (a + b + c) are in standard order • However, (b + a + c) is NOT in standard order (a + c) does NOT contain all variables • Minterms (a b c) and (a b c) are in standard order • However, (b a c) is not in standard order (a c) does not contain all variables 31

Sum-Of-Minterm (SOM) § Sum-Of-Minterm (SOM) canonical form: Sum of minterms of entries that evaluate to ‘ 1’ x y z F 0 0 1 1 0 1 0 1 0 1 0 0 1 1 Minterm m 1 = x y z Focus on the ‘ 1’ entries m 6 = x y z m 7 = x y z F = m 1 + m 6 + m 7 = ∑ (1, 6, 7) = x y z + x y z 32

Sum-Of-Minterm Examples § F(a, b, c, d) = ∑(2, 3, 6, 10, 11) § F(a, b, c, d) = m 2 + m 3 + m 6 + m 10 + m 11 abcd+abcd+abcd § G(a, b, c, d) = ∑(0, 1, 12, 15) § G(a, b, c, d) = m 0 + m 12 + m 15 abcd+abcd+abcd 33

Product-Of-Maxterm (POM) § Product-Of-Maxterm (POM) canonical form: Product of maxterms of entries that evaluate to ‘ 0’ x y z F 0 0 1 1 0 1 0 1 1 1 0 1 0 1 Maxterm M 2 = (x + y + z) Focus on the ‘ 0’ entries M 4 = (x + y + z) M 6 = (x + y + z) F = M 2·M 4·M 6 = ∏ (2, 4, 6) = (x+y+z) 34

Product-Of-Maxterm Examples § F(a, b, c, d) = ∏(1, 3, 6, 11) § F(a, b, c, d) = M 1 · M 3 · M 6 · M 11 (a+b+c+d) § G(a, b, c, d) = ∏(0, 4, 12, 15) § G(a, b, c, d) = M 0 · M 4 · M 12 · M 15 (a+b+c+d) 35

Observations § We can implement any function by "ORing" the minterms corresponding to the ‘ 1’ entries in the function table. A minterm evaluates to ‘ 1’ for its corresponding entry. § We can implement any function by "ANDing" the maxterms corresponding to ‘ 0’ entries in the function table. A maxterm evaluates to ‘ 0’ for its corresponding entry. § The same Boolean function can be expressed in two canonical ways: Sum-of-Minterms (SOM) and Product-of. Maxterms (POM). § If a Boolean function has fewer ‘ 1’ entries then the SOM canonical form will contain fewer literals than POM. However, if it has fewer ‘ 0’ entries then the POM form will have fewer literals than SOM. 36

Converting to Sum-of-Minterms Form § A function that is not in the Sum-of-Minterms form can be converted to that form by means of a truth table § Consider F = y + x z x y z F Minterm 0 0 1 1 1 1 0 0 m 0 = x y z m 1 = x y z m 2 = x y z 0 0 1 1 0 1 0 1 m 4 = x y z m 5 = x y z F = ∑(0, 1, 2, 4, 5) = m 0 + m 1 + m 2 + m 4 + m 5 = xyz+xyz+xyz 37

Converting to Product-of-Maxterms Form § A function that is not in the Product-of-Minterms form can be converted to that form by means of a truth table § Consider again: F = y + x z x y z F 0 0 1 1 1 1 0 0 1 1 0 1 0 1 Minterm F = ∏(3, 6, 7) = M 3 · M 6 · M 7 = M 3 = (x+y+z) M 6 = (x+y+z) M 7 = (x+y+z) 38

Conversions Between Canonical Forms x y z F 0 0 1 1 0 1 0 1 0 1 1 1 0 1 Minterm Maxterm M 0 = (x + y + z) m 1 = x y z m 2 = x y z m 3 = x y z M 4 = (x + y + z) m 5 = x y z M 6 = (x + y + z) m 7 = x y z F = m 1+m 2+m 3+m 5+m 7 = ∑(1, 2, 3, 5, 7) = xyz+xyz+xyz F = M 0 · M 4 · M 6 = ∏(0, 4, 6) = (x+y+z)(x+y+z) 39

Algebraic Conversion to Sum-of-Minterms § Expand all terms first to explicitly list all minterms § AND any term missing a variable v with (v + v) § Example 1: f = x + x y (2 variables) f = x (y + y) + x y f=xy+xy+xy f = m 3 + m 2 + m 0 = ∑(0, 2, 3) § Example 2: g = a + b c (3 variables) g = a (b + b)(c + c) + (a + a) b c g=abc+abc+abc+abc g=abc+abc+abc g = m 1 + m 4 + m 5 + m 6 + m 7 = ∑ (1, 4, 5, 6, 7) 40

Algebraic Conversion to Product-of-Maxterms § Expand all terms first to explicitly list all maxterms § OR any term missing a variable v with v · v § Example 1: f = x + x y (2 variables) Apply 2 nd distributive law: f = (x + x) (x + y) = 1 · (x + y) = M 1 § Example 2: g = a c + b c + a b (3 variables) g = (a c + b c + a) (a c + b) (distributive) g = (c + b c + a) (a c + b) (x + x y = x + y) g = (c + b + a) (a + c + b) (x + x y = x + y) g = (a + b + c) = M 5. M 2 = ∏ (2, 5) 41

Function Complements § The complement of a function expressed as a sum of minterms is constructed by selecting the minterms missing in the sum-of-minterms canonical form § Alternatively, the complement of a function expressed by a Sum of Minterms form is simply the Product of Maxterms with the same indices § Example: Given F(x, y, z) = ∑ (1, 3, 5, 7) F(x, y, z) = ∑ (0, 2, 4, 6) F(x, y, z) = ∏ (1, 3, 5, 7) 42

Summary of Minterms and Maxterms § There are 2 n minterms and maxterms for Boolean functions with n variables. § Minterms and maxterms are indexed from 0 to 2 n – 1 § Any Boolean function can be expressed as a logical sum of minterms and as a logical product of maxterms § The complement of a function contains those minterms not included in the original function § The complement of a sum-of-minterms is a product-ofmaxterms with the same indices 43

Standard Forms § Standard Sum-of-Products (SOP) form: equations are written as an OR of AND terms § Standard Product-of-Sums (POS) form: equations are written as an AND of OR terms § Examples: • SOP: A B C + B • POS: (A + B) · (A+ B + C )· C § These “mixed” forms are neither SOP nor POS • (A B + C) (A + C) • A B C + A C (A + B) 44

Standard Sum-of-Products (SOP) § A sum of minterms form for n variables can be written down directly from a truth table. • Implementation of this form is a two-level network of gates such that: • The first level consists of n-input AND gates • The second level is a single OR gate § This form often can be simplified so that the corresponding circuit is simpler. 45

Standard Sum-of-Products (SOP) § A Simplification Example: F( A, B, C) = S (1, 4, 5, 6, 7) § Writing the minterm expression: F = A B C + ABC § Simplifying: F = A B C + A (B C + B C) F = A B C + A (B (C + C) + B (C + C)) F = A B C + A (B + B) F=ABC+A F=BC+A § Simplified F contains 3 literals compared to 15 46

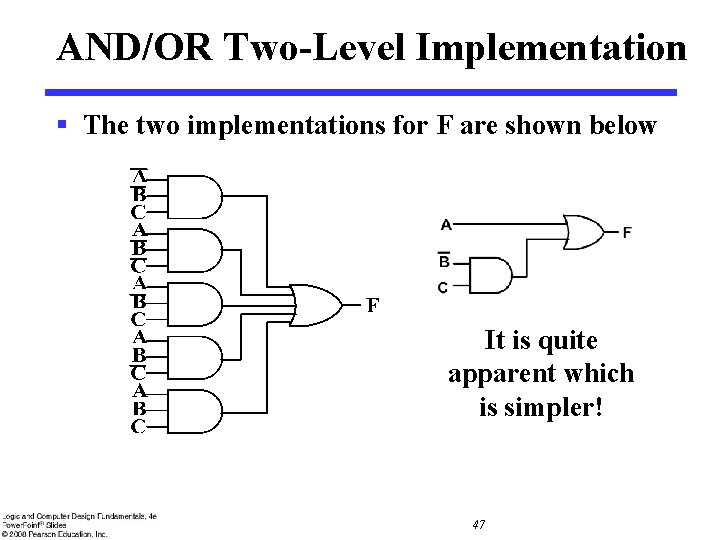
AND/OR Two-Level Implementation § The two implementations for F are shown below It is quite apparent which is simpler! 47

SOP and POS Observations § The previous examples show that: • Canonical Forms (Sum-of-minterms, Product-of-Maxterms), or other standard forms (SOP, POS) differ in complexity • Boolean algebra can be used to manipulate equations into simpler forms • Simpler equations lead to simpler implementations § Questions: • How can we attain a “simplest” expression? • Is there only one minimum cost circuit? • The next part will deal with these issues 48

Terms of Use § All (or portions) of this material © 2008 by Pearson Education, Inc. § Permission is given to incorporate this material or adaptations thereof into classroom presentations and handouts to instructors in courses adopting the latest edition of Logic and Computer Design Fundamentals as the course textbook. § These materials or adaptations thereof are not to be sold or otherwise offered for consideration. § This Terms of Use slide or page is to be included within the original materials or any adaptations thereof. 49