Logic and Computer Design Fundamental Chapter 1 Digital

Logic and Computer Design Fundamental Chapter 1 Digital and Computer Information M. Mano & Charles R. Kime 2008, Pearson Education, Inc 1

Overview • Sistem Komputer dan Sistem Digital • Representasi Informasi • Sistem Bilangan [biner, oktal dan heksadesimal] • Operasi Aritmatik • Dasar Konversi • Kode Desimal [BCD (binary coded decimal), parity] • Kode Gray • Kode Alphanumeric 2

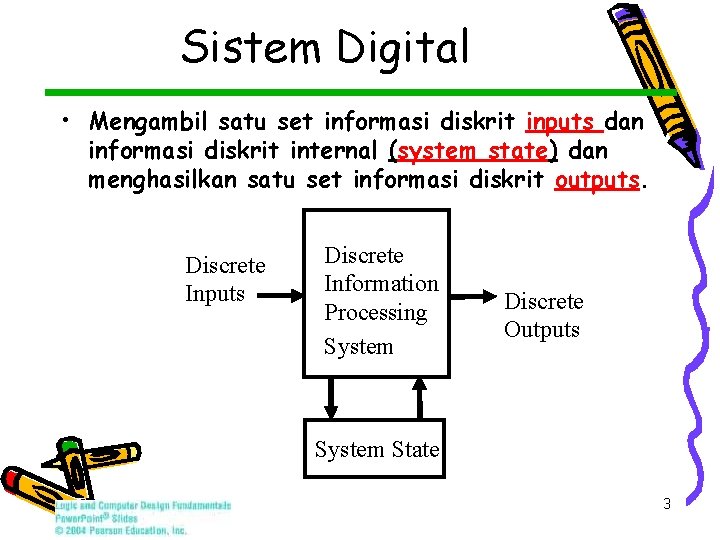
Sistem Digital • Mengambil satu set informasi diskrit inputs dan informasi diskrit internal (system state) dan menghasilkan satu set informasi diskrit outputs. Discrete Inputs Discrete Information Processing System Discrete Outputs System State 3

Tipe 2 dari sistem digital • Tanpa kondisi (No state present) – Sistem Logika kombinasi – Output = Fungsi (Input) • Dengan kondisi(State present) – Kondisi di-updated pada waktu diskrit => Sistem Urutan Synchronous – Kondisi di-updated setiap waktu => Sistem Urutan Asynchronous – Kondisi/keadaan = Function (Keadaan, Input) – Output = Fungsi (Keadaan) atau Fungsi Keadaan (Keadaan, Input) 4

Contoh Sistem Digital: Penghitung Digital (Digital Counter (e. g. , odometer): Count Up Reset 0 0 1 3 5 6 4 Inputs: Count Up, Reset Outputs: Visual Display "Value" of stored digits State: Synchronous or Asynchronous? 5

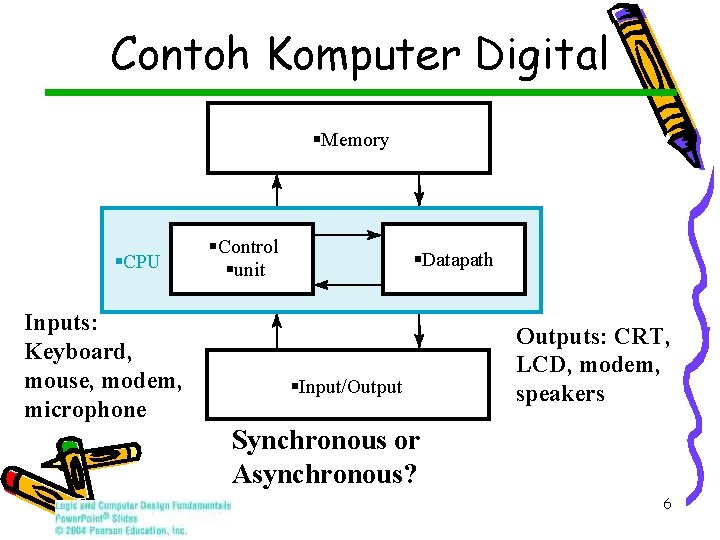
Contoh Komputer Digital §Memory §CPU Inputs: Keyboard, mouse, modem, microphone §Control §unit §Datapath §Input/Outputs: CRT, LCD, modem, speakers Synchronous or Asynchronous? 6

Sinyal • Suatu variabel informasi yang dinyatakan dengan besaran fisik. • Untuk Sistem digital, variabel diambil pada nilai diskrit. • Dua level, atau nilai biner yang umum dipakai sebagai nilai pada sistem digital. • Nilai Biner dinyatakan dengan : – – digits 0 and 1 words (symbols) False (F) and True (T) words (symbols) Low (L) and High (H) and words On and Off. • Nilai biner dapat juga dinyatakan dalam nilai atau range dari kwantitas fisik. 7

Nilai Biner: Kwantitas fisik yang lain • Sebutkan physical quantities yang lain yang menyatakan 0 and 1? – CPU Voltage – Disk Magnetic Field Direction – CD Surface Pits/Light – Dynamic RAM Electrical Charge 8

Kedepan…. Sistem Embedded • Komputer sebagai bagian integral dari produk yang lain. • Contoh dari komputer embedded – Microcomputers – Microcontrollers – Digital signal processors Chapter 1 9

Sistem Embedded • Contoh dari Aplikasi Sistem Embedded – – – – Cell phones Automobiles Video games Copiers Dishwashers Flat Panel TVs Global Positioning Systems Chapter 1 10

Embedded systems overview • Sistem komputasi ada di-mana. • Umumnya orang hanya berpikir tentang komputer “desktop” – – PC’s Laptops Mainframes Servers • Tetapi ternyata ada sistem yang lain dari tipe komputasi • Sejauh ini yang lebih dikenal…. . .

• Sistem Komputasi Embedded – Computing systems embedded within electronic devices – Hard to define. Nearly any computing system other than a desktop computer – Billions of units produced yearly, versus millions of desktop units – Perhaps 50 per household and per automobile Computers are in here. . . and here. . . and even here. . . Lots more of these, though they cost a lot less each.

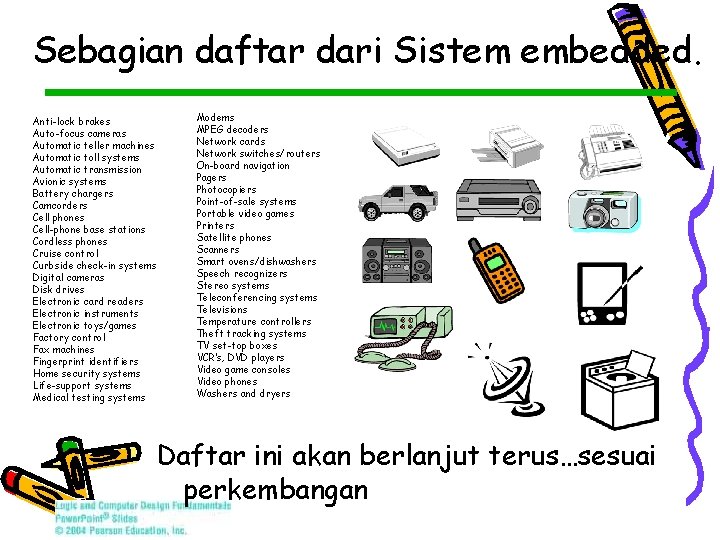
Sebagian daftar dari Sistem embedded. Anti-lock brakes Auto-focus cameras Automatic teller machines Automatic toll systems Automatic transmission Avionic systems Battery chargers Camcorders Cell phones Cell-phone base stations Cordless phones Cruise control Curbside check-in systems Digital cameras Disk drives Electronic card readers Electronic instruments Electronic toys/games Factory control Fax machines Fingerprint identifiers Home security systems Life-support systems Medical testing systems Modems MPEG decoders Network cards Network switches/routers On-board navigation Pagers Photocopiers Point-of-sale systems Portable video games Printers Satellite phones Scanners Smart ovens/dishwashers Speech recognizers Stereo systems Teleconferencing systems Televisions Temperature controllers Theft tracking systems TV set-top boxes VCR’s, DVD players Video game consoles Video phones Washers and dryers Daftar ini akan berlanjut terus…sesuai perkembangan

Tiga kunci teknologi sistem embedded. q Teknologi Suatu penyelesaian tugas/pekerjaan terutama dengan menggunakan technical processes, metode 2, atau pengetahuan q Tiga kunci teknologi sistem embedded. – IC technology – Processor technology – Design technology

Representasi Sistem Bilangan • Radix Positif, positional sistem bilangan • Suatu bilangan dengan radix r adalah menyatakan untaian dari digit: A n - 1 A n - 2 … A 1 A 0. A - 1 A - 2 … A - m + 1 A - m yang mana 0 £ Ai < r dan. Adalah titik radix • Untaian digit menyatakan urutan pangkat. j=-1 i=n-1 (Number)r = ( å i=0 Ai r + )( i å j=-m Aj r ) j (Integer Portion) + (Fraction Portion) 15

Contoh – Sistem Bilangan Radix (Basis) Digits Pangkat dr Radix 0 1 2 3 4 5 -1 -2 -3 -4 -5 Umum Desimal Biner r 10 2 0 => r - 1 0 => 9 0 => 1 r 0 r 1 r 2 r 3 r 4 r 5 r -1 r -2 r -3 r -4 r -5 1 10 1000 10, 000 100, 000 0. 1 0. 001 0. 00001 1 2 4 8 16 32 0. 5 0. 25 0. 125 0. 0625 0. 03125 16

Pangkat Spesial dari 2 § 210 (1024) is Kilo, denoted "K" § 220 (1, 048, 576) is Mega, denoted "M" § 230 (1, 073, 741, 824)is Giga, denoted "G" 17

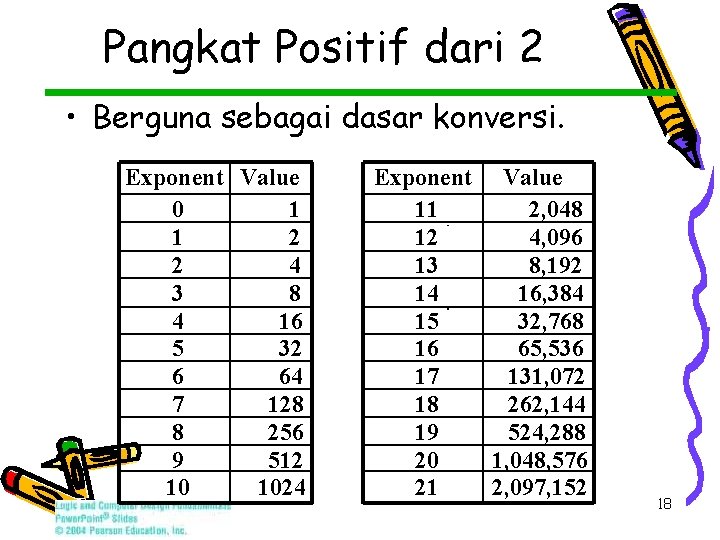
Pangkat Positif dari 2 • Berguna sebagai dasar konversi. Exponent Value 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 Exponent Value 11 2, 048 12 4, 096 13 8, 192 14 16, 384 15 32, 768 16 65, 536 17 131, 072 18 262, 144 19 524, 288 20 1, 048, 576 21 2, 097, 152 18

Angka dengan dasar/basis yang berbeda • Bagus…sebagai bahan pengingat. Decimal (Base 10) 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 Binary (Base 2) 000001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 10000 Octal (Base 8) 00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 20 Hexadecimal (Base 16) 00 01 02 03 04 05 06 07 08 09 0 A 0 B 0 C 0 D 0 E 0 F 10 19

Hubungan pada Sistem Bilangan Sifat-sifat Sistem Desimal : a. Terdiri dari 10 bilangan pokok b. Pangkat terkecil (0), makin kekiri bertambah dengan 1 c. Koefisien : 0, 1, …. 10 d. Jika dalam satu kolom koefisien melebihi bil dasarnya pindah kekiri dengan penambahan 1 20

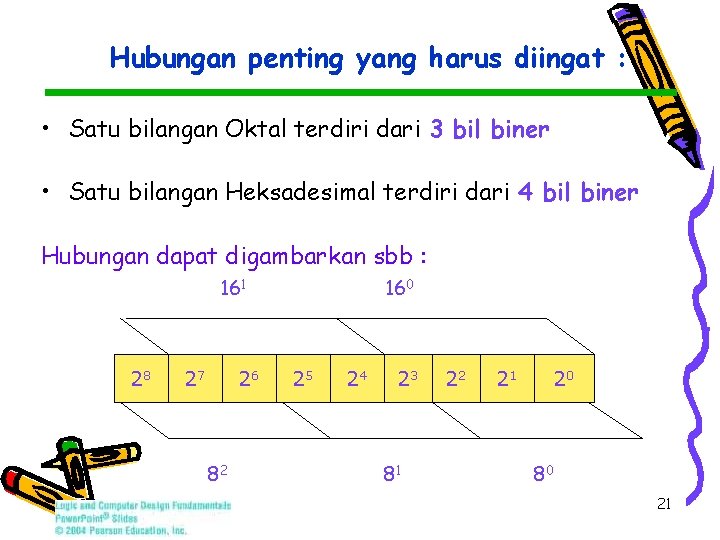
Hubungan penting yang harus diingat : • Satu bilangan Oktal terdiri dari 3 bil biner • Satu bilangan Heksadesimal terdiri dari 4 bil biner Hubungan dapat digambarkan sbb : 161 28 27 26 82 160 25 24 23 81 22 21 20 80 21

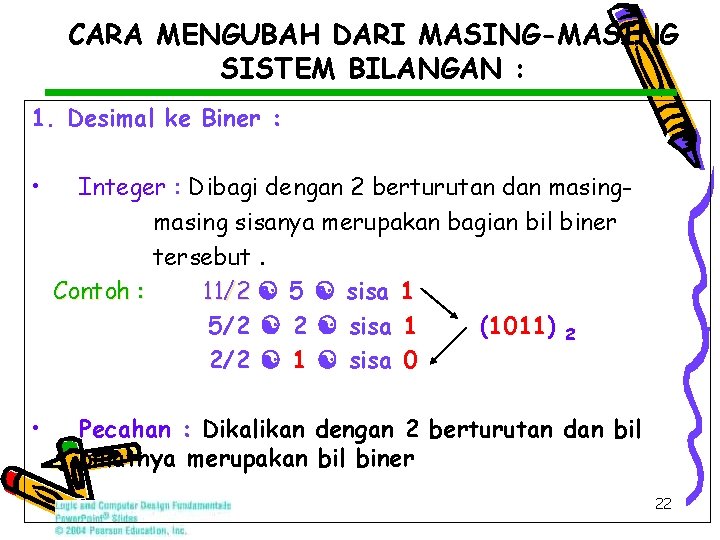
CARA MENGUBAH DARI MASING-MASING SISTEM BILANGAN : 1. Desimal ke Biner : • • Integer : Dibagi dengan 2 berturutan dan masing sisanya merupakan bagian bil biner tersebut. Contoh : 11/2 5 sisa 1 5/2 2 sisa 1 (1011) 2 2/2 1 sisa 0 Pecahan : Dikalikan dengan 2 berturutan dan bil bulatnya merupakan bil biner 22

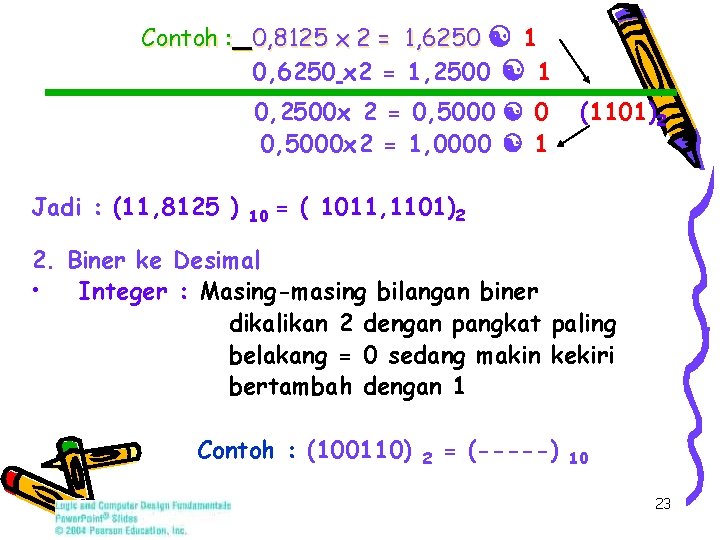
Contoh : 0, 8125 x 2 = 1, 6250 1 0, 6250 x 2 = 1, 2500 1 0, 2500 x 2 = 0, 5000 0 0, 5000 x 2 = 1, 0000 1 Jadi : (11, 8125 ) 10 (1101)2 = ( 1011, 1101)2 2. Biner ke Desimal • Integer : Masing-masing bilangan biner dikalikan 2 dengan pangkat paling belakang = 0 sedang makin kekiri bertambah dengan 1 Contoh : (100110) 2 = (-----) 10 23

(100110)2 = 1 x 25 + 0 x 24 +0 x 23+1 x 22+1 x 21+0 x 20 = 32 + 4 + 2 = 38 • Pecahan : Masing-masing bil biner dikalikan 2, dan pamgkatnya paling depan = 0, makin kekanan berkurang dengan 1 Contoh : (0. 1101)2 + (…………. ) 10 (0. 1101) 2 = 0 x 20+1 x 2 -1+1 x 2 -2+0 x 2 -3+1 x 2 -4 = 0, 5 + 0, 25 + 0, 0625 = 0, 8125 24

3. Oktal ke Biner: Masing-masing bil diterjemahkan dalam biner dan tiap bilangan harus terdiri dari 3 bil biner Contoh : (7314) 8 7 3 (111) (011) 1 (001) 4 (100) (111 001 100 )2 4. Desimal ke Oktal : Analog dengan butir 1 dengan bil dasar 8 5. Oktal ke Desimal : Analog dengan butir 2 dengan bil dasar 8 25

Untuk Heksadesimal ke Biner, Desimal ke Heksadesimal serta Heksadesimal ke Desimal Analog dengan butir 3, 4, 5 CARA PERHITUNGAN PADA SISTEM BINER: Penjumlahan : Contoh : 0+1 = 1 1 0 yang ditambah 0+0 = 0 1 1 1 penambah 1+0 = 1 1 0 1 Jumlah 1+1 = (1) 0 Pengurangan : analogi dengan penjumlahan hanya ada ‘pinjaman’ bila diperlukan 26

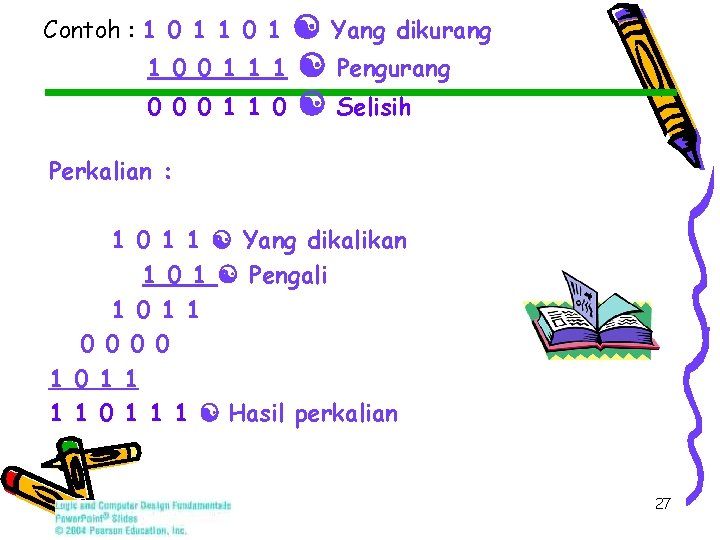
Yang dikurang 1 Pengurang 0 Selisih Contoh : 1 0 1 1 0 0 0 1 1 Perkalian : 1 0 1 1 Yang dikalikan 1 0 1 Pengali 1 0 1 1 0 0 1 0 1 1 1 Hasil perkalian 27

Konversi Biner ke Desimal • Untuk mengkonversi ke desimal, gunakan aritmatika desimal untuk membentuk: S (digit × respective power of 2). • Example: Convert 110102 to N 10: 28

Konversi Desimal ke Biner • Metode ke-1 – Subtract the largest power of 2 that gives a positive remainder and record the power. – Repeat, subtracting from the prior remainder and recording the power, until the remainder is zero. – Place 1’s in the positions in the binary result corresponding to the powers recorded; in all other positions place 0’s. • Example: Convert 62510 to N 2 29

Dasar Umum sistem bilangan Nama Radix Digits Biner 2 0, 1 Oktal 8 0, 1, 2, 3, 4, 5, 6, 7 Desimal 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Heksadesimal 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F § Enam huruf (penambahan dari angka integer 10) dalam heksadesimal menyatakan: A – F = 10 - 15 30

Konversi antar Dasar (basis) § Metode 2 Untuk mengkonversi dari satu basis ke yang lain. 1) Konversikan bag integer 2) Konversikan bag pecahan 3) Gabung kedua hasil dengan radix point 31

Konversi secara detail • Mengkonversi bag integer. Berulang bagilah angka dengan radix yang baru dan simpan sisanya. Digit dengan radix baru adalah sisa yang didapat dengan di-urutkan berlawanan. Bila radix yang baru > 10, kemudian konversikan semua sisa > 10 ke digit A, B, … • Mengkonversi bag integer. pecahan Berulang kalikan bag pecahan dengan radix yang baru dan simpan hasil yang integer. Digit untuk radix yang baru adalah digit integer sesuai urutan. Apabila radix yang baru > 10, kemudian konversikan integer> 10 ke digit A, B, … 32

Contoh: • Konversikan 46. 687510 ke basis 2 • Konversikan 46 ke basis 2 • Konversikan 0. 6875 ke basis 2 : • Gabungkanlah hasilnya dengan radix point: 33

Keterangan Tambahan- Bag Pecahan • Catatan bahwa dalam mengkonversi, bag pecahan akan menjadi 0 sebagai hasil dari pengulangan • Umumnya , bisa terjadi tetapi bisa juga tidak terjadi. • Contoh: Konversikan 0. 6510 ke N 2 – 0. 65 = 0. 101001001 … – Bag pecahan akan berulang setiap 4 step dan mengulang 1001 selamanya! • Penyelesaian: Pastikan jumlah bit yang benar, bulatkan atau hilangkan yang lain. 34

Mengecek hasil konversi • Untuk mengkonversi balik, jumlahkan perkalian digit dengan pangkat yang sesuai dari r. • Dari konversi yang lalu: 46. 687510 1011102 = 1· 32 + 0· 16 +1· 8 +1· 4 + 1· 2 +0· 1 = 32 + 8 + 4 + 2 = 46 0. 10112 = 1/2 + 1/8 + 1/16 = 0. 5000 + 0. 1250 + 0. 0625 = 0. 6875 35

Oktal (Heksadesimal) ke Biner dan sebaliknya • Oktal (Heksadesimal) to Biner: – Buatlah setiap Oktal (heksadesimal) menjadi tiga(empat) digit biner mulai dari radix point ke-kedua arah. • Biner ke Oktal (Heksadesimal): – Group-kan digit biner menjadi tiga (empat) bit group mulai dari radix point ke-kedua arah. Tambahkan nol bila dibutuhkan pada bag pecahan. – Konversikan masing 2 group dari tiga (empat) ke oktal (heksadesimal) digit. 36

Oktal to Heksadesimal lewat Biner • Konversikan oktal • Gunakan grouping seperti diatas ke • Contoh: Oktal ke ( 6 3 5 ke biner. empat bit dan konversikan heksadesimal digits. Biner ke Heksadesimal. 1 7 7 ) 8 • Bagaimana konversi ini bisa bekerja? 37

Catatan Terakhir Konversi • Sebetulnya dapat pula dilakukan aritmatika dalam basis yang lain, tapi harus dsangat hati 2. • Contoh: Konversikan 1011102 ke basis 10 menggunakan aritmatika biner : Step 1 101110 / 1010 = 100 r 0110 Step 2 100 / 1010 = 0 r 0100 Converted Digits are 01002 | 01102 or 4 6 10 38

Kode Biner untuk digit Desimal Lebih dari 8, 000 jalan yang dapat dipilih dari 10 elements ke 16 bilangan biner 4 bits. Yang sering digunakan adalah: Decimal 8, 4, 2, 1 0 1 2 3 4 5 6 7 8 9 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 Excess 3 8, 4, -2, -1 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 0000 0111 0110 0101 0100 1011 1010 1001 1000 1111 Gray 0000 0101 0110 0011 0001 1000 39

Binary Coded Decimal (BCD) • Kode BCD adalah kode 8, 4, 2, 1. • This code is the simplest, most intuitive binary code for decimal digits and uses the same powers of 2 as a binary number, but only encodes the first ten values from 0 to 9. • Example: 1001 (9) = 1000 (8) + 0001 (1) • How many “invalid” code words are there? • What are the “invalid” code words? 40

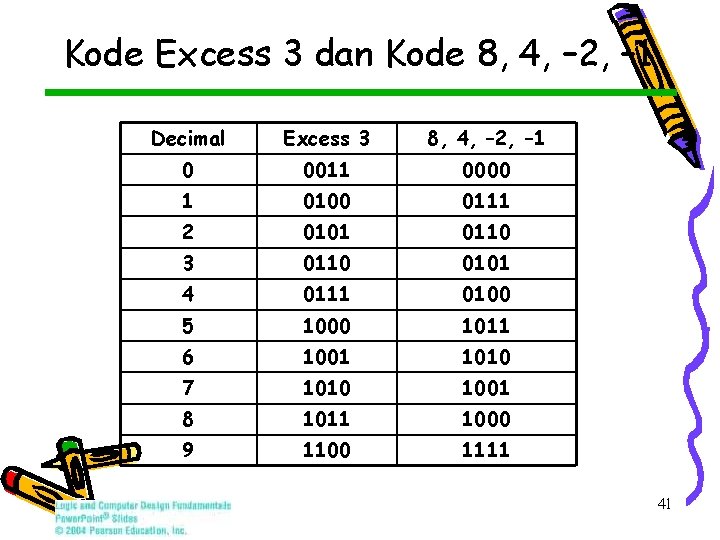
Kode Excess 3 dan Kode 8, 4, – 2, – 1 Decimal Excess 3 8, 4, – 2, – 1 0 0011 0000 1 0100 0111 2 0101 0110 3 0110 0101 4 0111 0100 5 1000 1011 6 1001 1010 7 1010 1001 8 1011 1000 9 1100 1111 41

Gray Code Decimal 8, 4, 2, 1 Gray 0 1 2 3 4 5 6 7 8 9 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 0000 0101 0110 0011 0001 1000 • What special property does the Gray code have in relation to adjacent decimal digits? 42

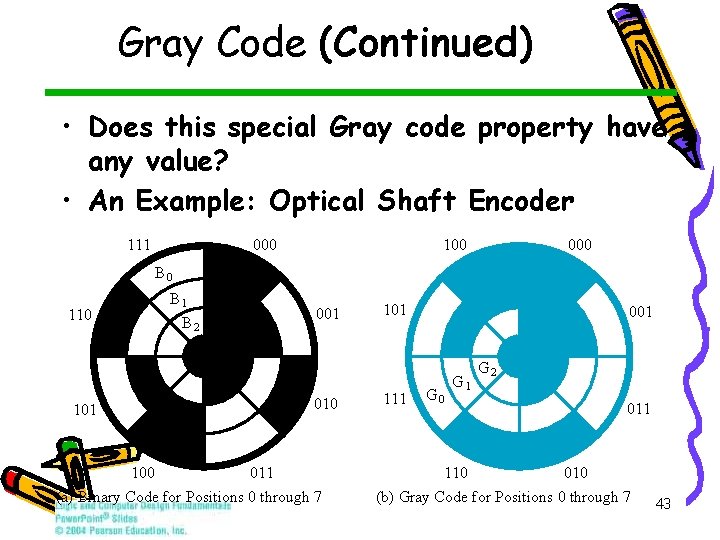
Gray Code (Continued) • Does this special Gray code property have any value? • An Example: Optical Shaft Encoder 111 000 100 000 B 1 110 001 B 2 010 101 100 011 (a) Binary Code for Positions 0 through 7 101 111 001 G 0 G 1 G 2 011 110 010 (b) Gray Code for Positions 0 through 7 43

Gray Code (Continued) • How does the shaft encoder work? • For the binary code, what codes may be produced if the shaft position lies between codes for 3 and 4 (011 and 100)? • Is this a problem? 44

• Answer 1: The encoder disk contains opaque and clear areas. • Opaque represents a 0 and clear a 1. Light shining through each ring of the encoder corresponding to a bit of the code strikes a sensor to produce a 0 or a 1. • Answer 2: In addition to the correct code, either 011 or 100, the codes 000, 010, 001, 110, 101, or 111 can be produced. • Answer 3: Yes, the shaft position can be completely UNKNOWN! 45

Gray Code (Continued) • For the Gray code, what codes may be produced if the shaft position lies between codes for 2 and 6 (010 and 110)? • Is this a problem? • Does the Gray code function correctly for these borderline shaft positions for all cases encountered in octal counting? 46

• Answer 1: Only the correct codes, either 010 or 110 • Answer 2: No, the shaft position is known to be either 3 or 4 which is OK since it is halfway in between. • Answer 3: Yes, since an erroneous code cannot arise. This includes between 0 and 7 (000 and 100). 47

Perhatian: Konversi atau Coding? • Jangan Bingung antara konversi dari bilangan desimal ke biner dengan coding suatu bilangan desimal ke BINARY CODE. • 1310 = 11012 (Ini adalah konversi) • 13 0001|0011(Ini adalah coding) 48

Aritmatika BCD Suatu BCD code, dijumlahkan dengan aritmatika biner: 8 1000 Eight +5 +0101 Plus 5 13 1101 is 13 (> 9) Catatan bahwa hasik adalah > 9, seharusnya dinyatakan dalam 2 digit Untuk mengkoreksi, tambahkan 6 modulo 16. 8 1000 Eight +5 +0101 Plus 5 13 1101 is 13 (> 9) +0110 so add 6 carry = 1 0011 leaving 3 + cy 0001 | 0011 Final answer (two digits) § If the digit sum is > 9, add one to the next significant digit 49

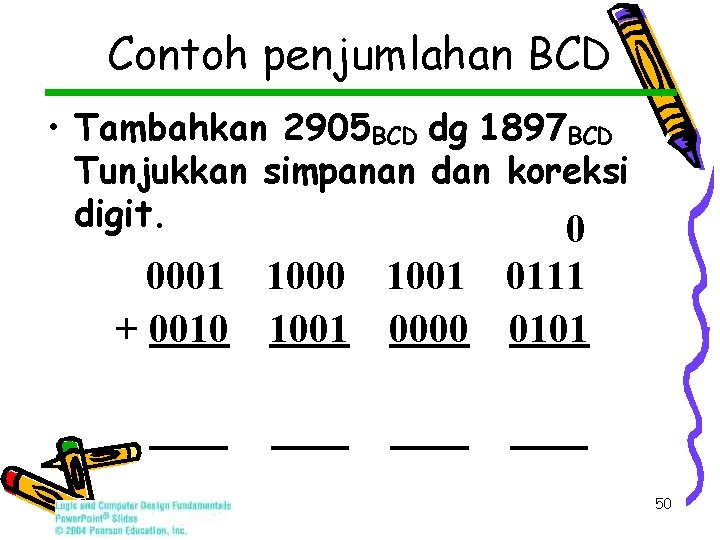
Contoh penjumlahan BCD • Tambahkan 2905 BCD dg 1897 BCD Tunjukkan simpanan dan koreksi digit. 0 0001 1000 1001 0111 + 0010 1001 0000 0101 50

Error-Detection Codes • Redundancy (e. g. extra information), in the form of extra bits, can be incorporated into binary code words to detect and correct errors. • A simple form of redundancy is parity, an extra bit appended onto the code word to make the number of 1’s odd or even. Parity can detect all single-bit errors and some multiple-bit errors. • A code word has even parity if the number of 1’s in the code word is even. • A code word has odd parity if the number of 1’s in the code word is odd. 51

4 -Bit Parity Code Example • Fill in the even and odd parity bits: Even Parity Odd Parity Message - Parity 000 001 010 011 100 101 110 111 - • The codeword "1111" has even parity and the codeword "1110" has odd parity. Both can be used to represent 3 -bit data. 52

ASCII Character Codes (Refer to Table 1 -4 in the text) • American Standard Code for Information Interchange • This code is a popular code used to represent information sent as character-based data. It uses 7 -bits to represent: – 94 Graphic printing characters. – 34 Non-printing characters • Some non-printing characters are used for text format (e. g. BS = Backspace, CR = carriage return) • Other non-printing characters are used for record marking and flow control (e. g. STX 53 and ETX start and end text areas).

ASCII Properties ASCII has some interesting properties: § Digits 0 to 9 span Hexadecimal values 3016 to 3916. § Upper case A-Z span 4116 to 5 A 16. § Lower case a-z span 6116 to 7 A 16. • Lower to upper case translation (and vice versa) occurs by flipping bit 6. § Delete (DEL) is all bits set, a carryover from when punched paper tape was used to store messages. § Punching all holes in a row erased a mistake! 54

UNICODE • UNICODE extends ASCII to 65, 536 universal characters codes – For encoding characters in world languages – Available in many modern applications – 2 byte (16 -bit) code words – See Reading Supplement – Unicode on the Companion Website http: //www. prenhall. com/mano 55