Logarithmic Functions and Their Graphs Consider This is

Consider This is a one-to-one function, therefore it has an inverse. The inverse is

Definition of Logarithmic Function b > 0; b 1 Logarithmic Form Exponential Form y

The log to the base “b” of “x” is the exponent to which “b”

Change from Logarithmic To Exponential Form Log 2 8 = 3 Log 25 5

Change from Exponential To Form Logarithmic 49 = 7 2 log 7 49 =

Properties of Logarithmic Functions If b, M, and N are positive real numbers, b

The Decibel Scale The decibel level D of a sound of intensity I ,

The Richter Scale The magnitude M on the Richter scale of an earthquake that

Since logs and exponentials are inverses the domain and range switch!…the x values and

Logarithmic Function with Base 2 y f y = 2 x 10 5 –

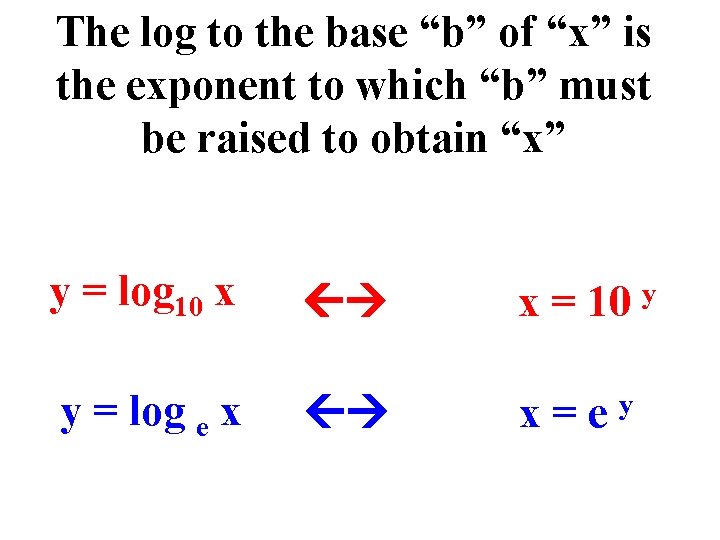
Slides: 12

Download presentation

Logarithmic Functions and Their Graphs

Consider This is a one-to-one function, therefore it has an inverse. The inverse is called a logarithm function. Example: Two raised to what power is 16? The most commonly used bases for logs are 10: and e: is called the natural log function. is called the common log function.

Definition of Logarithmic Function b > 0; b 1 Logarithmic Form Exponential Form y = logb x x = by

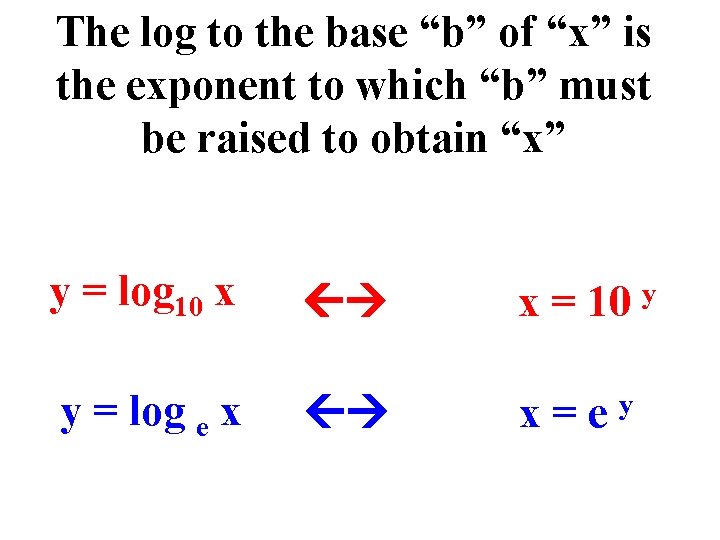
The log to the base “b” of “x” is the exponent to which “b” must be raised to obtain “x” y = log 10 x x = 10 y = log e x x=ey y

Change from Logarithmic To Exponential Form Log 2 8 = 3 Log 25 5 = ½ 8= 3 2 5 = 25 ½

Change from Exponential To Form Logarithmic 49 = 7 2 log 7 49 = 2 1/5 = 5 – 1 log 5 (1/5) = -1

Properties of Logarithmic Functions If b, M, and N are positive real numbers, b 1, and p and x are real numbers, then: Log 15 1 = 0 0 15 = 1 Log 10 10 = 1 101 = 10 Log 5 5 x = x 5 x = 5 x 3 log 3 x = x

The Decibel Scale The decibel level D of a sound of intensity I , measured in watts per square meter (W/ m 2) is given by where I 0 = 10– 12 W/ m 2 is the intensity of the least audible sound that an average healthy person can hear. Sound Intensity, W/ m 2 1. 0 10– 12 5. 2 10– 10 3. 2 10– 6 8. 5 10– 4 3. 2 10– 3 1. 0 100 8. 3 102 Sound Threshold of hearing Whisper Normal conversation Heavy traffic Jackhammer Threshold of pain Jet plane with afterburner

The Richter Scale The magnitude M on the Richter scale of an earthquake that releases energy E , measured in joules, is given by where E 0 = 104. 40 joules is the energy released by a small reference earthquake. Magnitude on Richter scale 4. 5 5. 5 6. 5 7. 5 < < M M M < < 4. 5 5. 5 6. 5 7. 5 Destructive power Small Moderate Large Major Greatest

Since logs and exponentials are inverses the domain and range switch!…the x values and y values are exchanged…

Logarithmic Function with Base 2 y f y = 2 x 10 5 – 5 5 f – 1 f y =x f -1 x = 2 y or y = log 2 x x 10 x y =2 x x=2 y – 1 1 8 1 4 1 2 0 1 2 3 1 2 4 8 – 3 – 2 Ordered pairs reversed DOMAIN of f = (– , ) = RANGE of f -1 -1 f f = (0, ) = DOMAIN of RANGE of y – 3 – 2 – 1 0 1 2 3