Localized Topology Control Algorithms for Heterogeneous Wireless Networks

Localized Topology Control Algorithms for Heterogeneous Wireless Networks Ning Li and Jennifer C. Hou University of Illinois at Urbana-Champaign Presented by Andrew Tzakis

The Goal l Increase the energy efficiency and Network capacity in wireless ad hoc networks and wireless sensor networks.

How to Reach this Goal l Create a topology control algorithm to improve energy efficiency and network connectivity. – Modify each node to use the lowest transmission power that will maintain the same level of network connectivity. l Benefits: Energy efficiency will obtained by not transmitting at max power. – Spatial reuse and mitigate MAC-level contention will both be improved. – Connectivity preserved. –

Related work l Most of the current algorithms assume Homogeneous Networks. – l This is not realistic, even identical radios can have different ranges. Rodoplu and Meng (R&M) can work on Heterogeneous network – – But is later shown to not be as efficient. Also the resulting topology is sensitive to the model used in computation.

Proposed Solutions l Li and Hou propose two localized topology control algorithms for heterogeneous wireless mutli-hop networks. – – Directed Relative Neighborhood Graph (DRNG) Directed Local Spanning Subgraph (DLSS)

Characteristics of DRNG and DLSS l DRNG and DLSS derive topologies with Smaller average node degress (both logical and physical. – l Reduces MAC level contection (for better throughput). They also produce smaller average link lengths while maintaining network connectivity. – Smaller link lengths implies smaller transmission power needed (creating better efficiency).

What needs to be proved l Li and Hou prove the following: 1. 2. 3. The topology derived under DRNG or DLSS preserves network connectivity. The out-degree of any node in the topology by DLSS or DRNG is bounded by a constant. The topology generated by DRNG or DLSS preserves network bi-directionality.

How DRNG and DLSS work 1. Information Collection – 2. Topology Construction – 3. Each node locally collects the information of the neighborhood. Each node creates a proper set of neighbors for the final topology using information from step 1. Construction of topology with only bidirectional links (optional) – Each node adjusts its set of neighbors to make sure all edges are reachable.

Information Collection l Each node needs to know all of the edges in its neighborhood.

Information Collection (2) l l This can be found by having all nodes broadcast using is maximal power a hello message that has a unique node id and its max transmit power. After each node collects its reachable neighborhood, it can broadcast this information so that each node has E(GR) for the whole graph. – This is needed for the next step, topology construction.

Weight Function u 1 1 5 5 3 v 1 u 2 2 v 2

Topology Construction DRNG

Topology Construction DLSS 3: If there is no path then add it 6: Once all paths have been reconnected, stop. An example will be shown in a few slides.

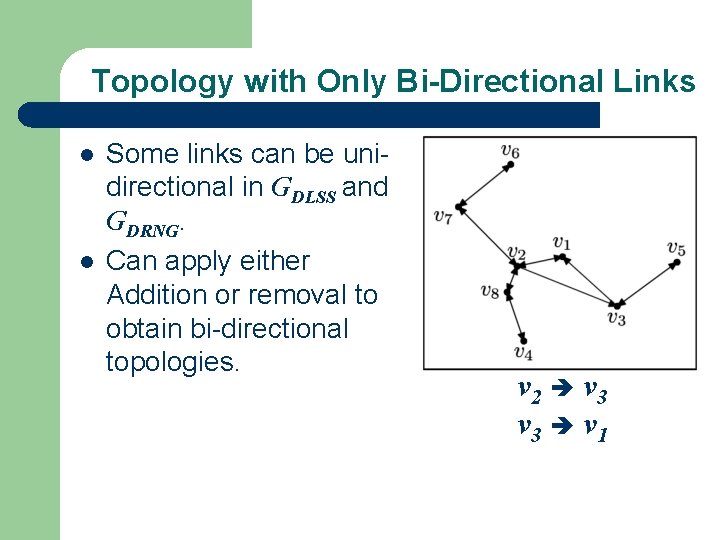
Topology with Only Bi-Directional Links l l Some links can be unidirectional in GDLSS and GDRNG. Can apply either Addition or removal to obtain bi-directional topologies. v 2 v 3 v 1

Addition And Removal l Addition – l Add an extra edge (v, u) into GA if (u, v) E(GA), (v, u) E(GA), and d(v, u) RV. Removal – Delete any edge (u, v) E(GA) if (v, u) E(GA)

The Proof l From earlier we need to prove 1. 2. 3. l The topology derived under DRNG or DLSS preserves network connectivity. The out-degree of any node in the topology by DLSS or DRNG is bounded by a constant. The topology generated by DRNG or DLSS preserves network bi-directionality. Assumptions: – G is always strongly connected.

1. Connectivity

1. Connectivity (2) Example of DLSS u 5 p 6 u 10 p ADD 10 u v ADD: Stop p reaches all nodes v Not Added v 6 5 p

1. Connectivity (3) GDRNG says p must exist for (u, v) not to be in the graph. However, if p exists then (u, v) would not be in GDLSS

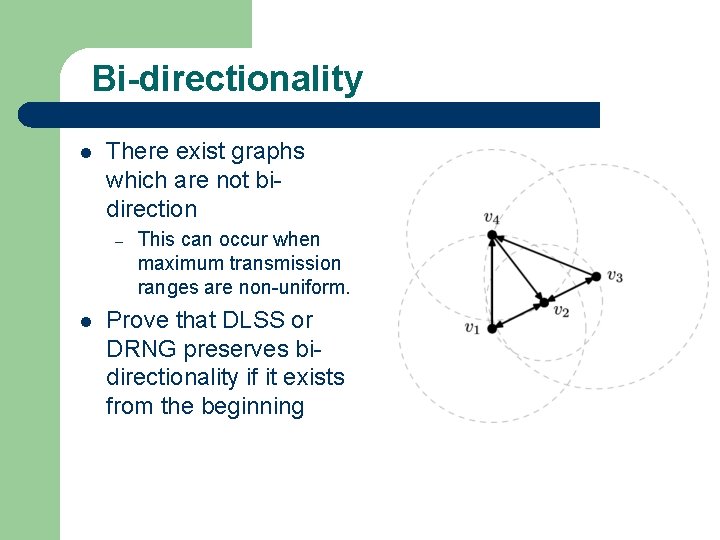
Bi-directionality l There exist graphs which are not bidirection – l This can occur when maximum transmission ranges are non-uniform. Prove that DLSS or DRNG preserves bidirectionality if it exists from the beginning

Bi-directionality(2)

Degree Bound l l The out-degree of a node u under algorithm A is denoted as deg. Aout(u) is the number of out-neighbors. The in-degree of u under algorithm A is denoted as deg. Ain(u) is the number of in-neighbors.

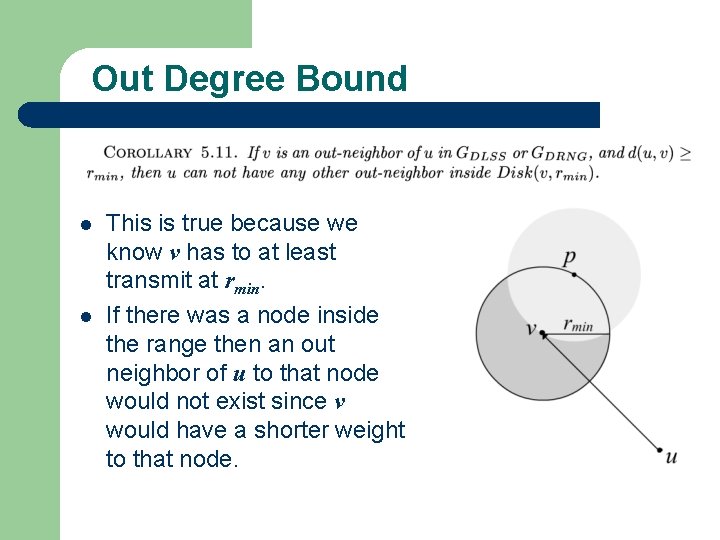
Out Degree Bound l l This is true because we know v has to at least transmit at rmin. If there was a node inside the range then an out neighbor of u to that node would not exist since v would have a shorter weight to that node.

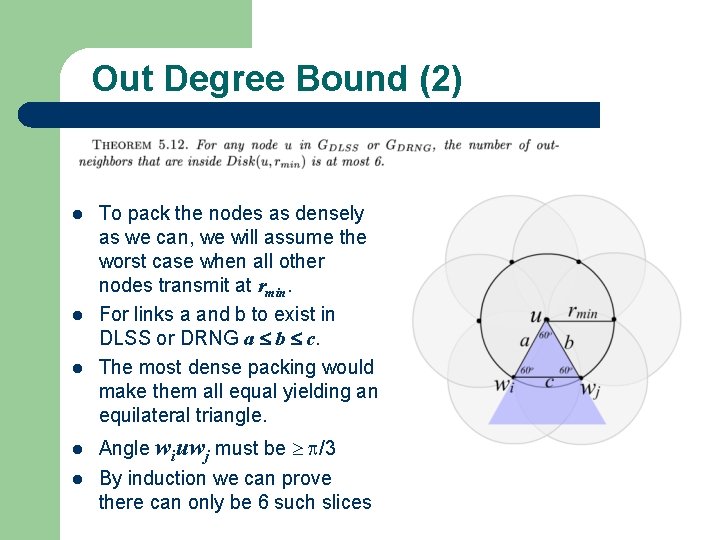
Out Degree Bound (2) l l l To pack the nodes as densely as we can, we will assume the worst case when all other nodes transmit at rmin. For links a and b to exist in DLSS or DRNG a b c. The most dense packing would make them all equal yielding an equilateral triangle. Angle wiuwj must be /3 By induction we can prove there can only be 6 such slices

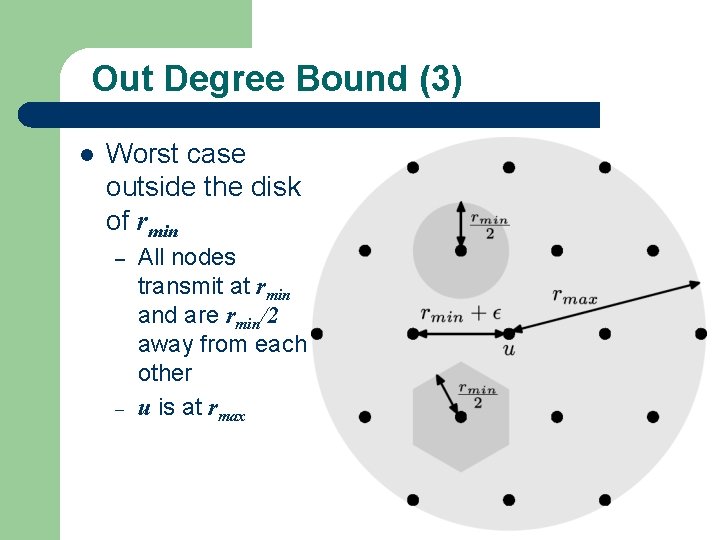
Out Degree Bound (3) l Worst case outside the disk of rmin – – All nodes transmit at rmin and are rmin/2 away from each other u is at rmax

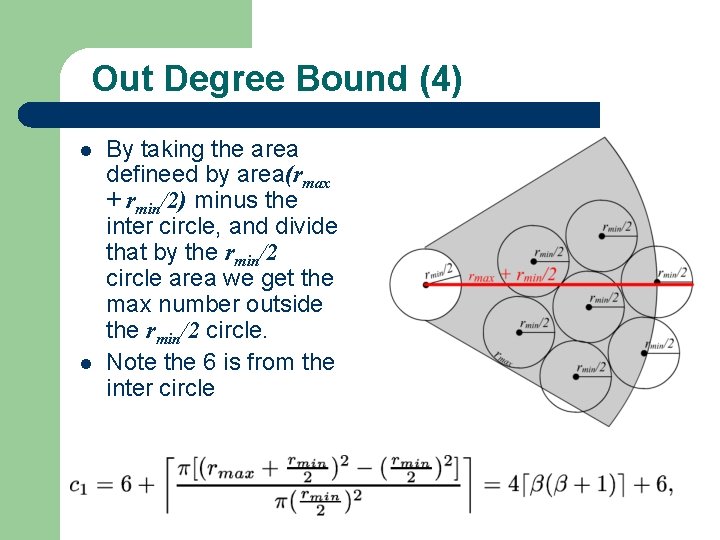
Out Degree Bound (4) l l By taking the area defineed by area(rmax + rmin/2) minus the inter circle, and divide that by the rmin/2 circle area we get the max number outside the rmin/2 circle. Note the 6 is from the inter circle

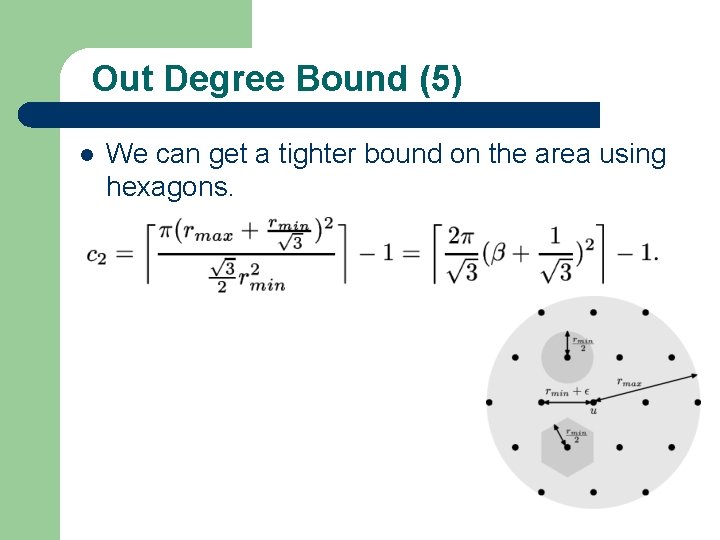
Out Degree Bound (5) l We can get a tighter bound on the area using hexagons.

In Degree Bound l In degree is similar to the inter circle, if you try to add a node p anywhere around the outside, the outside node would become the in node for p.

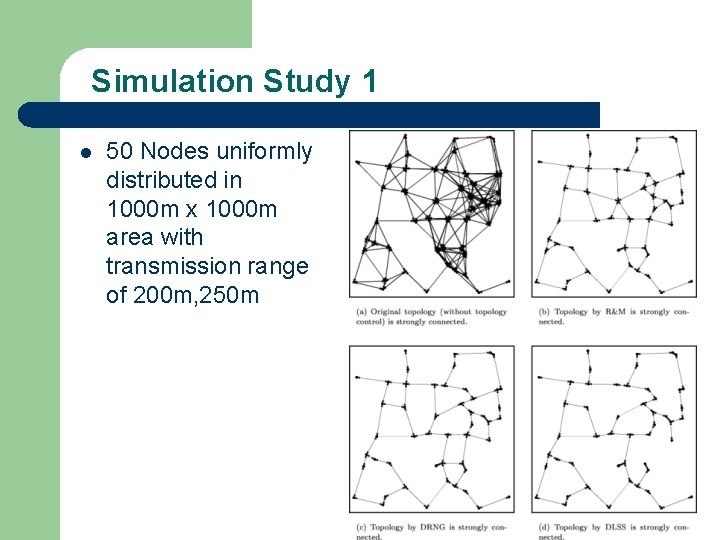
Simulation Study 1 l 50 Nodes uniformly distributed in 1000 m x 1000 m area with transmission range of 200 m, 250 m

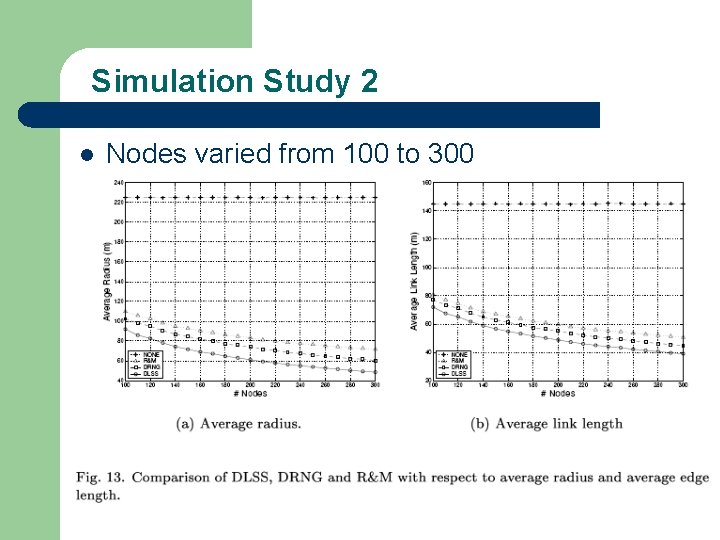
Simulation Study 2 l Nodes varied from 100 to 300

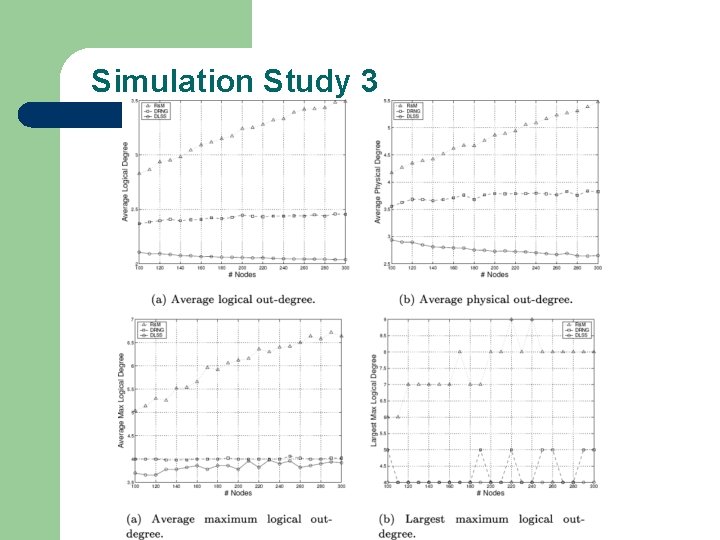
Simulation Study 3

Conclusion l DRNG and DLSS do the following for heterogeneous networks – – – l Preserve network connectivity Preserve network bi-directionality The out-degree of any node is bounded Simulation shows that DRNG and DLSS work much better that R&M.