Localization Navigation Announcement Robot Manipulator Lab will be

Localization & Navigation Announcement: Robot Manipulator Lab will be due the week of March 29 th

Computer with Wheels • Where am I? – Localization problem – Kidnapped robot problem • What way should I take to get there? – Path Planning (Pathing) • Where am I going? – Mission planning • Where have I been? – Map Making or Map Enhancement


Why is it difficult for a robot to know where it is? • Sensors are the fundamental input for the process of perception, therefore the degree sensors can discriminate the world state is critical • Sensor Aliasing – Many-to-one mapping between environmental states to the robot’s perceptual inputs – Amount of information is generally insufficient to identify the robot’s position from a single sensor reading

Why is it difficult for a robot to know where it is? • Sensor Noise – Adds a limitation on the consistency of sensor readings – Often the source of noise problems is that some environmental features are not captured by the robot’s representation. • Dynamic Environments • Unanticipated Events • Obstacle Avoidance

“Where am I”? • Localization – Given an initial estimate, q, of the robot’s location in configuration space, maintain an ongoing estimate of the robot pose with respect to the map, P(q). – Configuration Space (Cspace): data structure which allows the robot to specify its pose – Pose: (x, y, Θ)

Behavior Based Navigation • Can Robbie the Reactive Robot get from point A to point B?

Goal Directed Behavior Based Control How would Robbie navigate an office building?
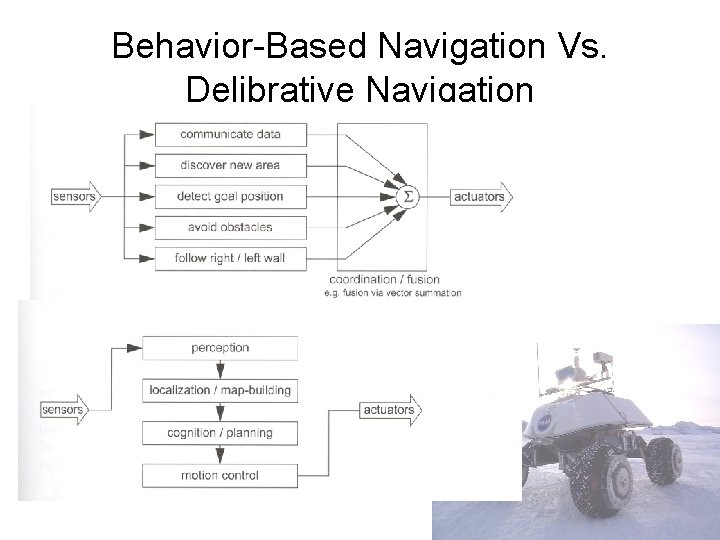
Behavior-Based Navigation Vs. Delibrative Navigation

The Cartographer: Spatial Memory • Data structures and methods for interpreting and storing sensory input with relation to the robot’s world – Representation of the world – Sensory input interpretation – Focus attention – Path planning & evaluation – Collection of information about the current environment

Map Representations • Quantitative (Metric Representations) • Topological (Landmarks) • Important considerations – Sufficiently represent the environment • Enough detail to navigate potential problems – Space and time complexity – Sufficiently represent the limitations of the robot – Support for map changes and re-planning – Compatibility with reactive layer

Many Types of Mobile Bases • Differential Drive – Two independently driven wheels on opposite sides of the robot – 3 Do. F: pose = [x, y, Θ] – Holonomic: can be treated as a massless point that can move in any direction

Types of Mobile Bases • Omni Drive – Wheel capable of rolling in any direction. – Robot can change direction without rotating the base

Types of Mobile Bases • Ackerman Drive – Typical car steering – Non-holonomic: must take into account position and velocity variable (can’t turn a car without moving it forward)
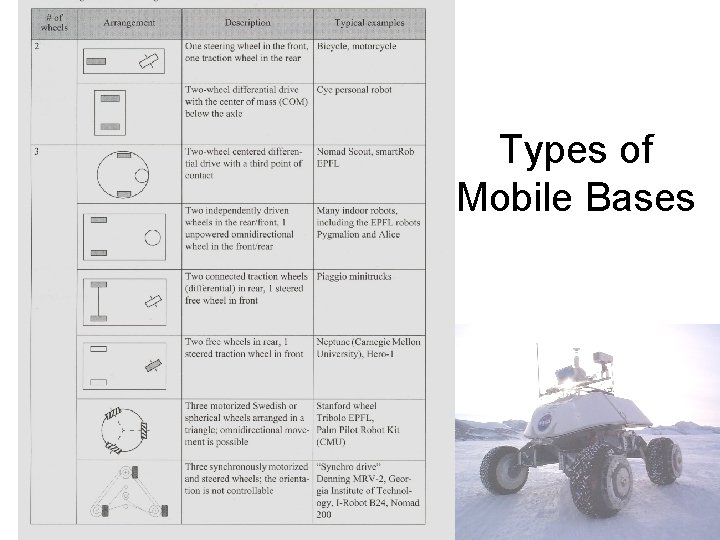
Types of Mobile Bases

Using Dead Reckoning to Estimate Pose • “ded reckoning” or deduced reckoning – Reckon: to determine by reference to a fixed basis • Keep track off the current position by noting how far the robot has traveled on a specific heading – Used for maritime navigation – Proprioceptive

Dead Reckoning with Shaft Encoders • How far has a wheel traveled? distance = 2 * PI * radius * #revolutions • Two types of wheel encoders reflectance sensor slot sensor

Wheel Encoders • Two types of wheel encoders reflectance sensor slot sensor • Note that there are two transitions per rotation

How is the Accuracy Determined?

Using Encoders with the HB • • Encoder functions defined in standard HB libraries Connect to ports 7, 8, 12, 13 (encoder# is 0, 1, 2, 3) enable_encoder(encoder#); – enable an encoder only once. . . unless you disable it between enables disable_encoder(encoder#); read_encoder(encoder#); – returns the number of transitions reset_encoder(encoder#); – sets that encoder’s count back to 0
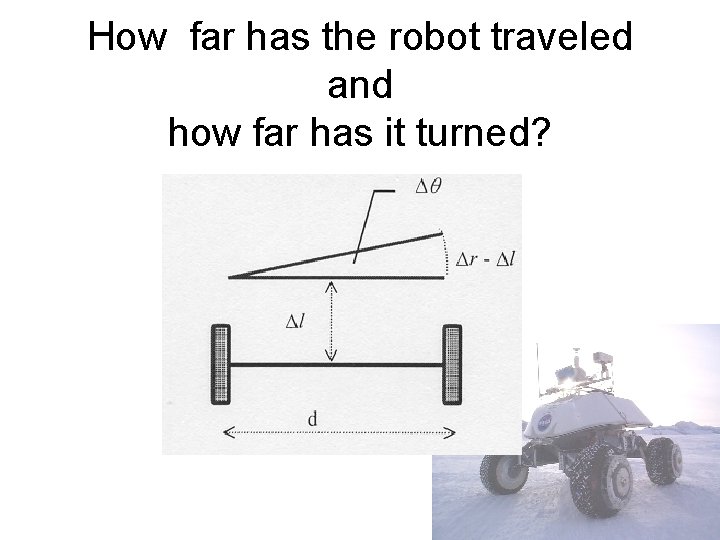
How far has the robot traveled and how far has it turned?

Which way am I going? • Heading – Percentage of the circumference of the circle with radius d

How far have I gone? • Half the distance of the arc at the end of the motion – Distance moved for center of the robot

Adding it up • (x, y, Θ) • Update the position information at each sensor update. • How large can a single segment be? • What does this assume?
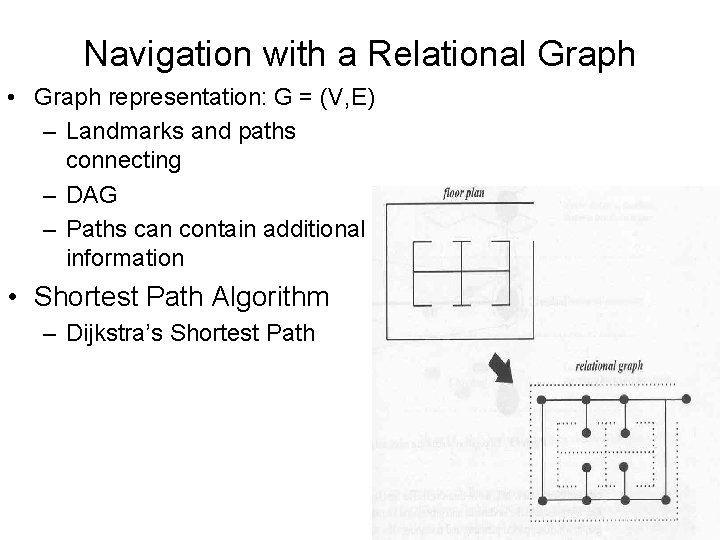
Navigation with a Relational Graph • Graph representation: G = (V, E) – Landmarks and paths connecting – DAG – Paths can contain additional information • Shortest Path Algorithm – Dijkstra’s Shortest Path

Example

Errors • Systematic Errors vs. Random Errors – Can they be managed?
- Slides: 27