Local Multiple Sequence Alignment Sequence Motifs Motifs Motifs

Local Multiple Sequence Alignment Sequence Motifs

Motifs • Motifs represent a short common sequence – Regulatory motifs (TF binding sites) – Functional site in proteins (DNA binding motif)

Regulatory Motifs • DNA in every cell is identical – Different cells have different functions • Transcription is crucial aspect of regulation – Transcription factors (TFs) affect transcription rates • TFs bind to regulatory motifs MCM 1 – Motifs are 6 – 20 nucleotides long MCM 1 – Activators and repressors motif – Usually located near target gene, mostly upstream SBF motif Transcription Start Site Gene X

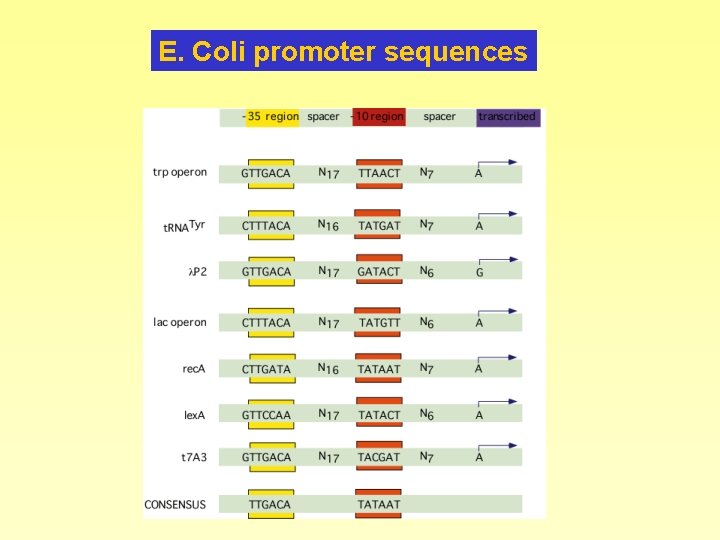
E. Coli promoter sequences

Challenges • How to recognize a regulatory motif? • Can we identify new occurrences of known motifs in genome sequences? • Can we discover new motifs within upstream sequences of genes?

1. Motif Representation • Exact motif: CGGATATA • Consensus: represent only deterministic nucleotides. – Example: HAP 1 binding sites in 5 sequences. • consensus motif: CGGNNNTANCGG • N stands for any nucleotide. • Representing only consensus loses information. How can this be avoided? CGGATATACCGG CGGTGATAGCGG CGGTACTAACGG CGGCGGTAACGG CGGCCCTAACGG ------CGGNNNTANCGG

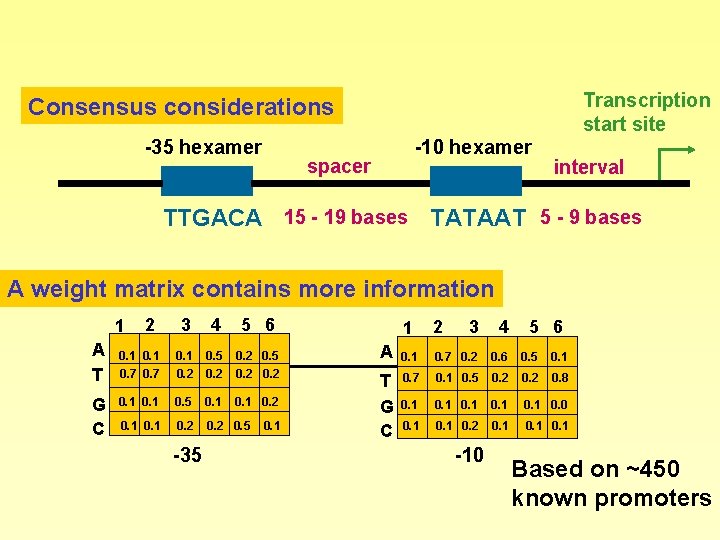
Transcription start site Consensus considerations -35 hexamer -10 hexamer spacer interval TTGACA 15 - 19 bases TATAAT 5 - 9 bases A weight matrix contains more information 3 4 5 6 0. 1 0. 7 0. 1 0. 2 0. 5 0. 2 0. 1 0. 5 0. 1 0. 2 0. 5 1 A T G C 2 -35 0. 1 A T G C 1 2 3 4 0. 1 0. 7 0. 2 0. 6 0. 5 0. 1 0. 7 0. 1 0. 5 0. 2 0. 8 0. 1 0. 0 0. 1 0. 2 0. 1 -10 5 6 Based on ~450 known promoters

PSPM – Position Specific Probability Matrix • Represents a motif of length k • Defines Pi{A, C, G, T} for i={1, . . , k}. – Pi (A) – frequency of nucleotide A in position i. 1 2 3 4 5 A 0. 1 0. 25 0. 05 0. 7 0. 6 C 0. 3 0. 25 0. 8 0. 15 T 0. 5 0. 25 0. 05 0. 1 0. 05 G 0. 1 0. 25 0. 1 0. 2

PSPM – Position Specific Probability Matrix • Represents a motif of length k • Defines Pi{A, C, G, T} for i={1, . . , k}. – Pi (A) – frequency of nucleotide A in position i. • Each k-mer is assigned a probability. – Example: P(TCCAG)=0. 5*0. 25*0. 8*0. 7*0. 2 1 2 3 4 5 A 0. 1 0. 25 0. 05 0. 7 0. 6 C 0. 3 0. 25 0. 8 0. 15 T 0. 5 0. 25 0. 05 0. 1 0. 05 G 0. 1 0. 25 0. 1 0. 2

Graphical Representation – Sequence Logo • Horizontal axis: position of the base in the sequence. • Vertical axis: amount of information. • Letter stack: order indicates importance. • Letter height: indicates frequency. • Consensus can be read across the top of the letter columns.

2. Identification of Known Motifs within Genomic Sequences • Motivation: – identification of new genes controlled by the same TF. – Infer the function of these genes. – enable better understanding of the regulation mechanism.

Detecting a Known Motif within a Sequence using PSPM • The PSPM is moved along the query sequence. • At each position the sub-sequence is scored for a match to the PSPM. 1 2 3 • Example: A 0. 1 0. 25 0. 05 sequence = ATGCAAGTCT… 4 5 0. 7 0. 6 C 0. 3 0. 25 0. 8 0. 15 T 0. 5 0. 25 0. 05 0. 1 0. 05 G 0. 1 0. 25 0. 1 0. 2

Detecting a Known Motif within a Sequence using PSPM • The PSPM is moved along the query sequence. • At each position the sub-sequence is scored for a match to the PSPM. 1 2 3 • Example: A 0. 1 0. 25 0. 05 sequence = ATGCAAGTCT… C 0. 3 0. 25 0. 8 • Position 1: ATGCA 0. 1*0. 25*0. 1*0. 6=1. 5*10 -4 4 5 0. 7 0. 6 0. 15 T 0. 5 0. 25 0. 05 0. 1 0. 05 G 0. 1 0. 25 0. 1 0. 2

Detecting a Known Motif within a Sequence using PSPM • The PSPM is moved along the query sequence. • At each position the sub-sequence is scored for a match to the PSPM. 1 2 3 • Example: A 0. 1 0. 25 0. 05 sequence = ATGCAAGTCT… C 0. 3 0. 25 0. 8 • Position 1: ATGCA 0. 1*0. 25*0. 1*0. 6=1. 5*10 -4 • Position 2: TGCAA 0. 5*0. 25*0. 8*0. 7*0. 6=0. 042 4 5 0. 7 0. 6 0. 15 T 0. 5 0. 25 0. 05 0. 1 0. 05 G 0. 1 0. 25 0. 1 0. 2

Detecting a Known Motif within a Sequence using PSSM Is it a random match, or is it indeed an occurrence of the motif? PSPM -> PSSM (Probability Specific Scoring Matrix) – odds score matrix: Oi(n) where n {A, C, G, T} for i={1, . . , k} – defined as Pi(n)/P(n), where P(n) is background frequency. Oi(n) increases => higher odds that n at position i is part of a real motif.

PSSM as Odds Score Matrix • Assumption: the background frequency of each nucleotide is 0. 25. 1 2 3 4 1. Original PSPM (Pi): A 0. 1 0. 25 0. 05 0. 7 2. Odds Matrix (Oi): A 5 0. 6 1 2 3 4 5 0. 4 1 0. 2 2. 8 2. 4 3. Going to log scale we get an additive score, Log odds Matrix (log 2 Oi): A 1 2 3 4 5 -1. 322 0 -2. 322 1. 485 1. 263

Calculating using Log Odds Matrix • Odds 0 implies random match; Odds > 0 implies real match (? ). • Example: sequence = ATGCAAGTCT… 1 2 • Position 1: ATGCA -1. 32+0 -1. 32+1. 26=-2. 7 odds= 2 -2. 7=0. 15 • Position 2: TGCAA 1+0+1. 68+1. 48+1. 26 =5. 42 odds=25. 42=42. 8 3 4 5 A -1. 32 0 -2. 32 1. 48 1. 26 C 0. 26 0 1. 68 -1. 32 -0. 74 T 1 0 -2. 32 -1. 32 -2. 32 G -1. 32 0 -1. 32 -0. 32

Calculating the probability of a Match ATGCAAG • Position 1 ATGCA = 0. 15

Calculating the probability of a Match ATGCAAG • Position 1 ATGCA = 0. 15 • Position 2 TGCAA = 42. 3

Calculating the probability of a Match ATGCAAG • Position 1 ATGCA = 0. 15 • Position 2 TGCAA = 42. 3 • Position 3 GCAAG = 0. 18

Calculating the probability of a match ATGCAAG • Position 1 ATGCA = 0. 15 • Position 2 TGCAA = 42. 3 • Position 3 GCAAG = 0. 18 P (i) = S / (∑ S) Example 0. 15 /(. 15+42. 8+. 18)=0. 003 P (1)= 0. 003 P (2)= 0. 993 P (3) =0. 004

Building a PSSM • Collect all known sequences that bind a certain TF. • Align all sequences (using multiple sequence alignment). • Compute the frequency of each nucleotide in each position (PSPM). • Incorporate background frequency for each nucleotide (PSSM).

PROBLEMS… • When searching for a motif in a genome using PSSM or other methods – the motif is usually found all over the place ->The motif is considered real if found in the vicinity of a gene. • Checking experimentally for the binding sites of a specific TF (location analysis) – the sites that bind the motif are in some cases similar to the PSSM and sometimes not!

3. Finding new Motifs • We are given a group of genes, which presumably contain a common regulatory motif. • We know nothing of the TF that binds to the putative motif. • The problem: discover the motif.

Difficulties in Computational Identification • Each motif can appear in any of m-k columns; there are (m-k)n possibilities. • Noise: Mismatches are allowed, the motif is not exact. Not all sequences contain the motif. • Statistical significance: k is short (6 -20 nucleotides). m ranges from 10 s (prokaryotes) to 1000 s (eukaryotes) of nucleotides. => a random motif can appear by chance in sequences.

Computational Methods • This problem has received a lot of attention from CS people. • Methods include: – Probabilistic methods – hidden Markov models (HMMs), expectation maximization (EM), Gibbs sampling, etc. – Enumeration methods – problematic for inexact motifs of length k>10. … • Current status: Problem is still open.

Tools on the Web • MEME – Multiple EM for Motif Elicitation. http: //meme. sdsc. edu/meme/website/ • meta. MEME- Uses HMM method http: //meme. sdsc. edu/meme • MAST-Motif Alignment and Search Tool http: //meme. sdsc. edu/meme • TRANSFAC - database of eukaryotic cis-acting regulatory DNA elements and trans-acting factors. http: //transfac. gbf. de/TRANSFAC/ • e. Motif - allows to scan, make and search for motifs in the protein level. http: //motif. stanford. edu/emotif/