Local Linear Matrix Factorization for Document Modeling Lu

Local Linear Matrix Factorization for Document Modeling Lu Bai, Jiafeng Guo, Yanyan Lan, Xueqi Cheng Institute of Computing Technology, Chinese Academy of Sciences bailu@software. ict. ac. cn

Outline n n Introduction Our approach Experimental results Conclusion

Introduction classification ranking recommendation

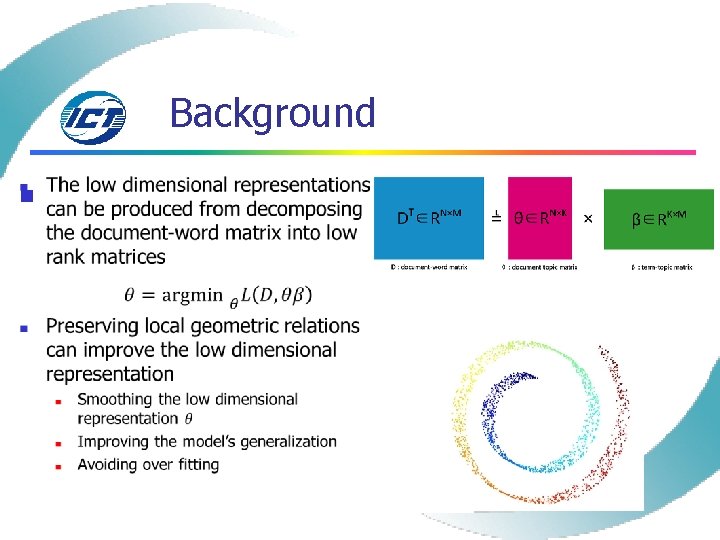
Background n

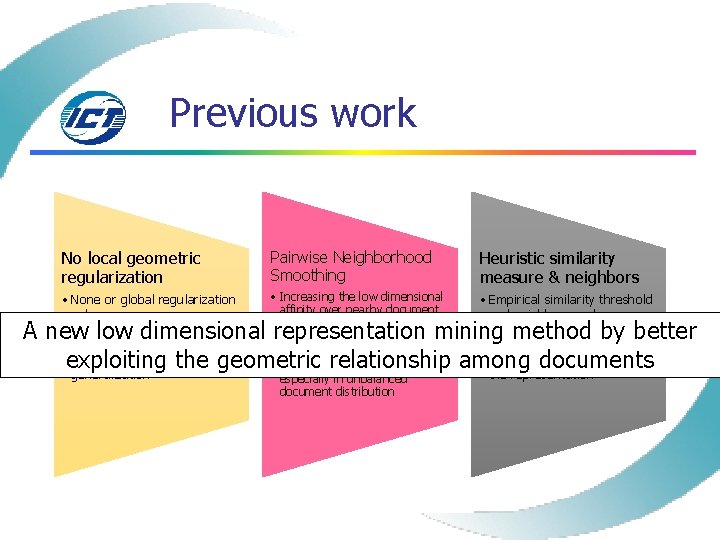
Previous work No local geometric regularization Pairwise Neighborhood Smoothing Heuristic similarity measure & neighbors • None or global regularization only • e. g. SVD, PLSA, LDA, NMF, etc. • Over-fitting & poor generalization • Increasing the low dimensional affinity over nearby document pairs • e. g. Lap. PLSA, LTM, DTM, etc. • Losing the geometric information among pairs, especially in unbalanced document distribution • Empirical similarity threshold and neighbor numbers • e. g. Lap. PLSA, LTM • Improper similarity measure or number of neighbors hurts the representation A new low dimensional representation mining method by better exploiting the geometric relationship among documents

Our approach n Basic ideas Mining low dimensional semantic representation • Factorizing document-word matrix in NMF way Preserving rich local geometric information • Modeling document’s relationships with local linear combination Selecting neighbors without similarity measure and threshold •

Local Linear Matrix Factorization(LLMF) n min

Cont’ n min

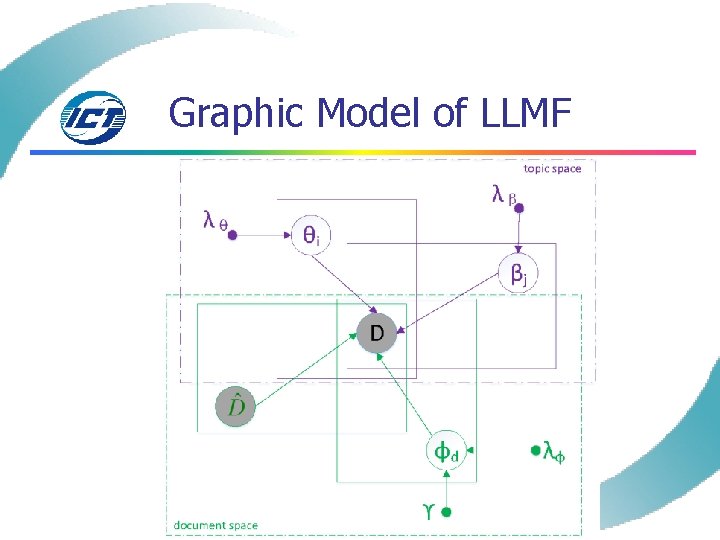
Graphic Model of LLMF

LLMF vs Others n Comparing models without geometric information n E. g. NMF, PLSA, LDA LLMF smoothes document representation with its neighbors Comparing models with geometric constraints n n n E. g. Lap. PLSA, LTM LLMF is free of similarity measure and neighborhood threshold LLMF is more robust in preserving local geometric structure in unbalanced data distribution

Model fitting n

Experimental Settings n Data set n n n 20 news & la 1(from Weka) Word Stemming Stop words removing Data sets Num. Of Document Num. of word Num. of category 20 news 18, 744 26, 214 20 la 1 2, 850 13, 195 5

Cont’ n

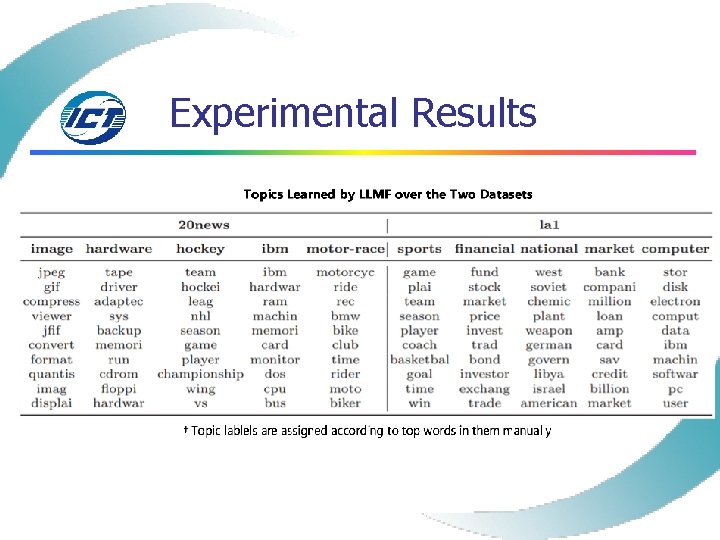
Experimental Results

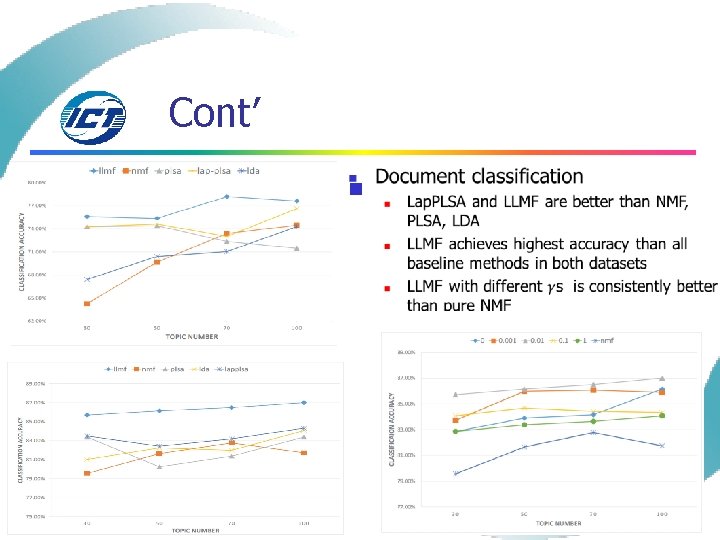
Cont’ n

Conclusion n Conclusions n n We propose a novel method, namely LLMF for learning low dimensional representations of document with local linear constraints. LLMF can better capture the rich geometric information among documents than those based on independent pairwise relationships. Experiments on benchmark of 20 news and la 1 show the proposed approach can learn better semantic representations compared to other baseline methods Future works n n We would extend LLMF to paralleled and distributed settings It is promising to apply LLMF in recommendation systems

References n n n D. M. Blei, A. Y. Ng, M. I. Jordan, and J. Lafferty. Latent dirichlet allocation. JMLR, 3: 2003, 2003. D. Cai, X. He, and J. Han. Locally consistent concept factorization for document clustering. TKDE, 23(6): 902– 913, 2011 D. Cai, Q. Mei, J. Han, and C. Zhai. Modeling hidden topics on document manifold. CIKM ’ 08, 911– 920, , NY, USA, 2008. ACM T. Hofmann. Unsupervised learning by probabilistic latent semantic analysis. In Machine Learning, page 2001, 2001 S. Huh and S. E. Fienberg. Discriminative topic modeling based on manifold learning. KDD ’ 10, pages 653– 662, New York, NY, USA, 2010. ACM

Thanks!! Q&A