Local Linear Approximation for Functions of Several Variables

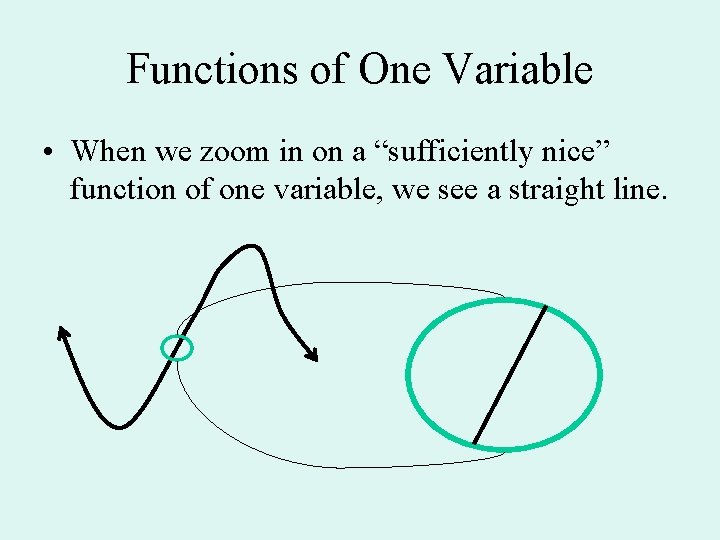
Functions of One Variable • When we zoom in on a “sufficiently nice” function of one variable, we see a straight line.

Functions of two Variables

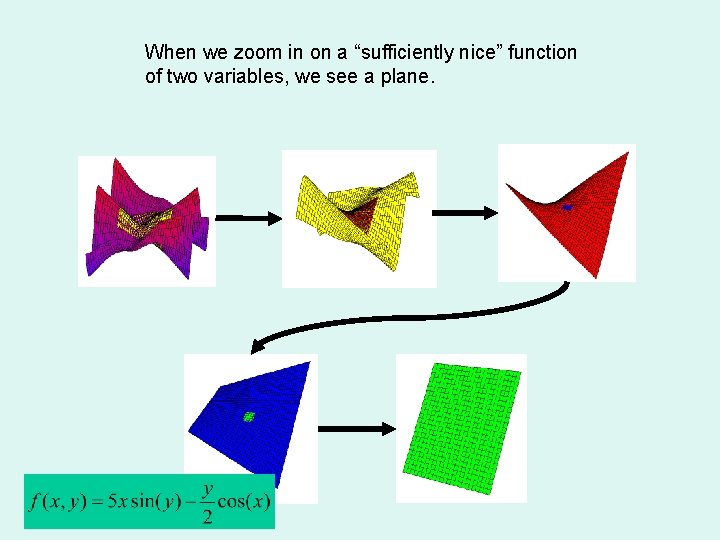
When we zoom in on a “sufficiently nice” function of two variables, we see a plane.

Describing the Tangent Plane • What information do we need to describe this plane? • The equation of the plane is • The point (a, b) and the partials of f in the x- and y-directions. • We can also write this in vector form. If we write and

General Linear Approximations In the expression we can think of the gradient as a scalar function on 2: This function is linear. For a general vector-valued function F: n → m and for a point p in n , we want to find a linear function Ap: n → m such that Why don’t we just subsume F(p) into Ap? Linear--- in the linear algebraic sense.

Linear Functions A function A is said to be linear provided that Note that A (0) = 0, since A(x) = A (x+0) = A(x)+A(0). For a function A: n → m, these requirements are very prescriptive.

Linear Functions It can be shown that if A: n → m is linear, then In other words, the function A is just left-multiplication by a matrix. Thus we cheerfully confuse the function A, with the matrix that represents it!

Local Linear Approximation For all x, we have F(x)=Ap(x-p)+F(p)+E(x) Where E(x) is the error committed by Lp(x)= Ap(x-p)+F(p) in approximating F(x)

Local Linear Approximation Fact: Suppose that F: n → m is given by coordinate functions F=(F 1, F 2 , . . . , Fm) and all the partial derivatives of F exist at p n , then. . . there is some matrix Ap such that F can be approximated locally near p by the affine function What can we say about the relationship between the matrix Ap and the coordinate functions F 1, F 2, F 3, . . . , Fm ? Quite a lot, actually. . .

We Just Compute First, I ask you to believe that if L=(L 1, L 2, . . . , Ln) for all i and j with 1 i n and 1 j m This should not be too hard. Why? Think about tangent lines, think about tangent planes. Considering now the matrix formulation, what is the partial of Lj with respect to xi?

The Derivative of F at p (sometimes called the Jacobian Matrix of F at p)

Local Linear Approximation So F will be “locally linear” if F(x) Df(p)(x-p)+F(p) for all x “close” to p. How close does x have to be to p? It is easy to see that for all x, we can find E(x) so that F(x)=Df(p)(x-p)+F(p)+E(x) is the error committed by Lp(x)= Df(p)(x-p)+F(p) in approximating F(x). How should we think about the error function E(x)?

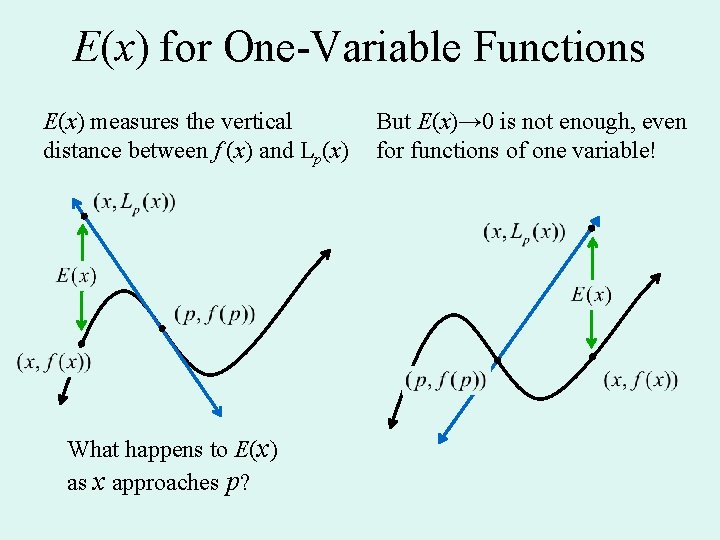
E(x) for One-Variable Functions E(x) measures the vertical distance between f (x) and Lp(x) What happens to E(x) as x approaches p? But E(x)→ 0 is not enough, even for functions of one variable!

Differentiability of Vector Fields A vector-valued function F: n → m is said to be differentiable provided that there exists a function E : n → m such that for all x, F(x)=Ap(x-p)+F(p)+E(x) where E(x) satisfies