Local Exact Pattern Matching for Nonfixed RNA Structures

Local Exact Pattern Matching for Non-fixed RNA Structures Mika Amit, Rolf Backofen, Steffen Heyne, Gad M. Landau, Mathias Mohl, Christina Schmiedl, Sebastian Will

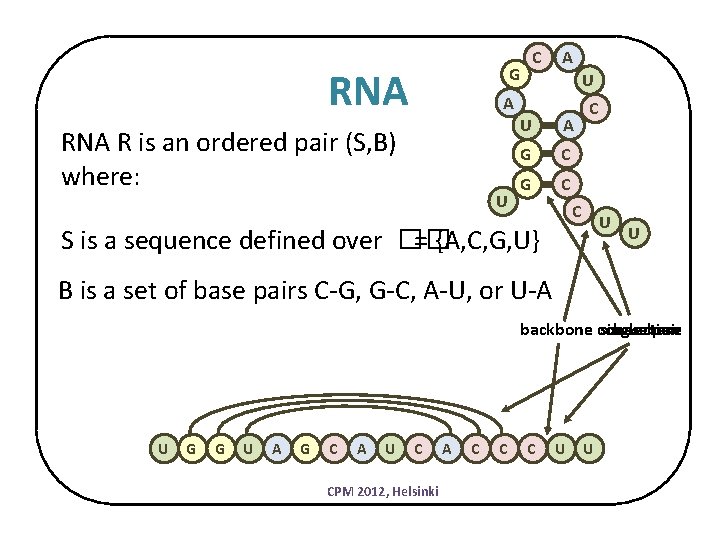
C G RNA A U A RNA R is an ordered pair (S, B) where: U U A G C C C U S is a sequence defined over �� = {A, C, G, U} U B is a set of base pairs C-G, G-C, A-U, or U-A backbone connection single base pair U G G U A G C A U C CPM 2012, Helsinki A C C C U U

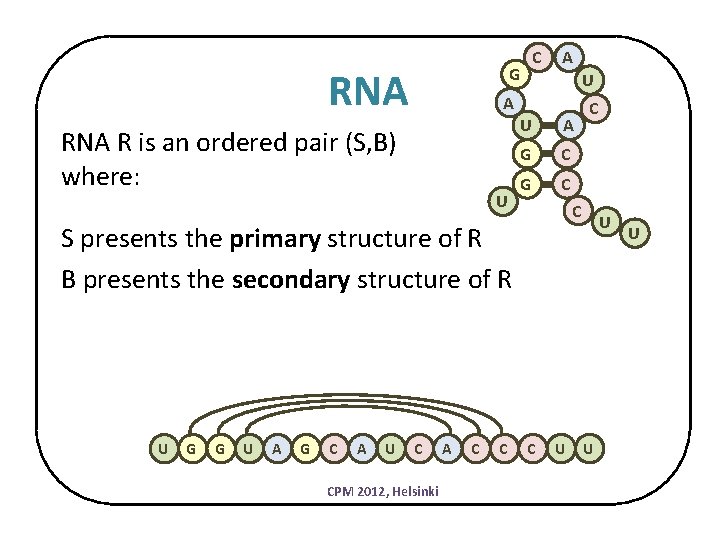
C G RNA A U A RNA R is an ordered pair (S, B) where: U U A G C C S presents the primary structure of R B presents the secondary structure of R U G G U A G C A U C CPM 2012, Helsinki A C C U U

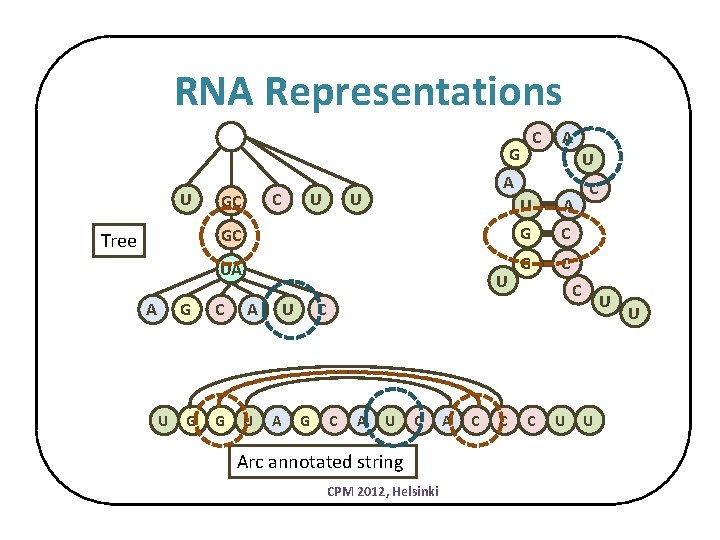
RNA Representations C G U Tree A G U G C GC U A U U A GC G C UA G C U C A G U U A C C G C A U C Arc annotated string CPM 2012, Helsinki A C C U U

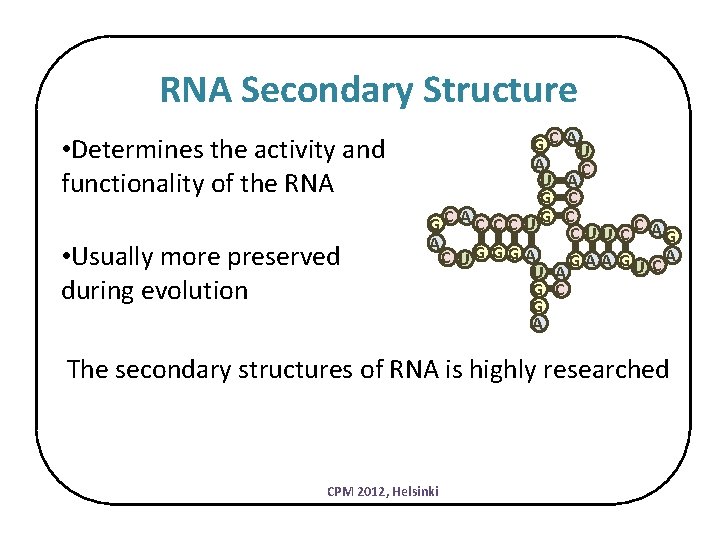
RNA Secondary Structure • Determines the activity and functionality of the RNA • Usually more preserved during evolution G C AU A C U A G C GC AC C C UG C C C U U C AG A C UG GG A A GU C A U A G C G A The secondary structures of RNA is highly researched CPM 2012, Helsinki

RNA Structure • Predicting the secondary structure of RNA molecule is a difficult task G C AU A C U A G C GC AC C C UG C C C U U C AG A C UG GG A A GU C A U A G C G A • The structure is sometimes given in a non-fixed form, where each base pair has a probability ≤ 1 to exist in the RNA CPM 2012, Helsinki

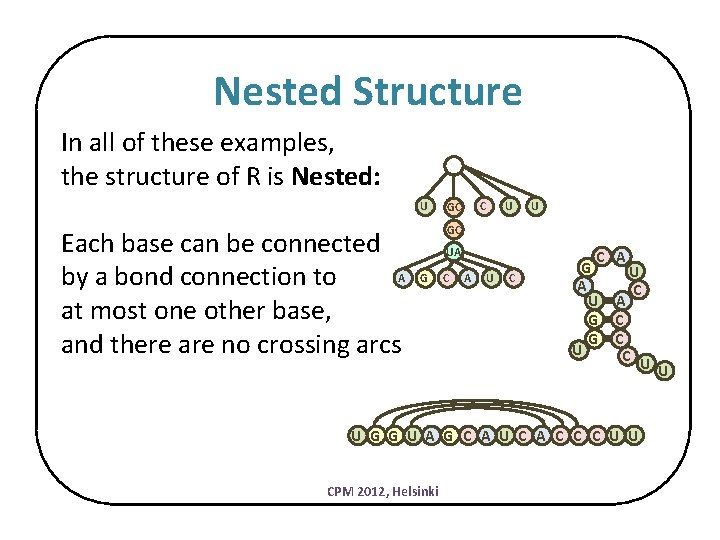
Nested Structure In all of these examples, the structure of R is Nested: U Each base can be connected A by a bond connection to at most one other base, and there are no crossing arcs C GC U U GC UA G C A U C C G A U G G U A U C A C C C U U U G G U A G C A U C A C C C U U CPM 2012, Helsinki

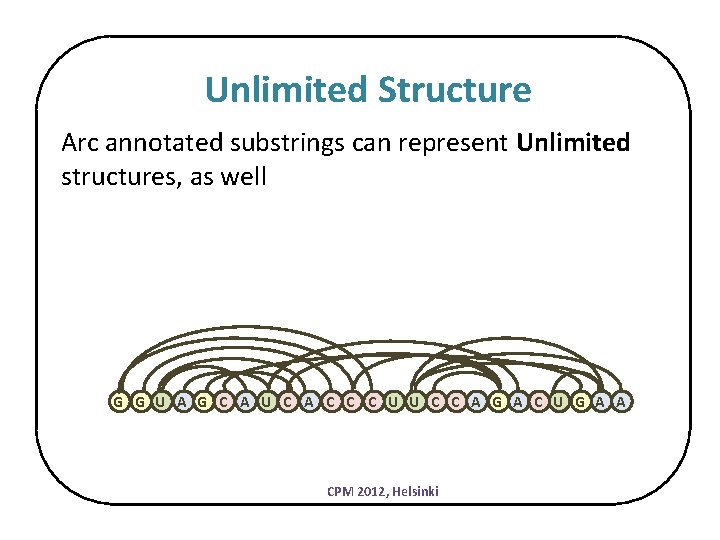
Unlimited Structure Arc annotated substrings can represent Unlimited structures, as well G G U A G C A U C A C C C U U C C A G A C U G A A CPM 2012, Helsinki

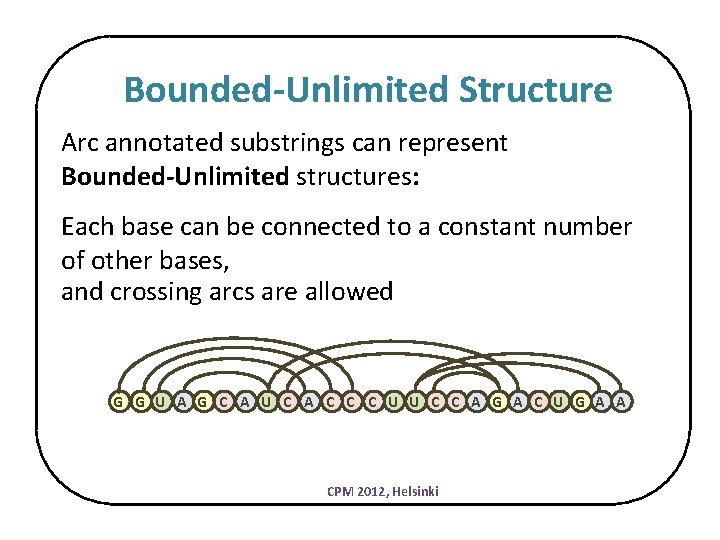
Bounded-Unlimited Structure Arc annotated substrings can represent Bounded-Unlimited structures: Each base can be connected to a constant number of other bases, and crossing arcs are allowed G G U A G C A U C A C C C U U C C A G A C U G A A CPM 2012, Helsinki

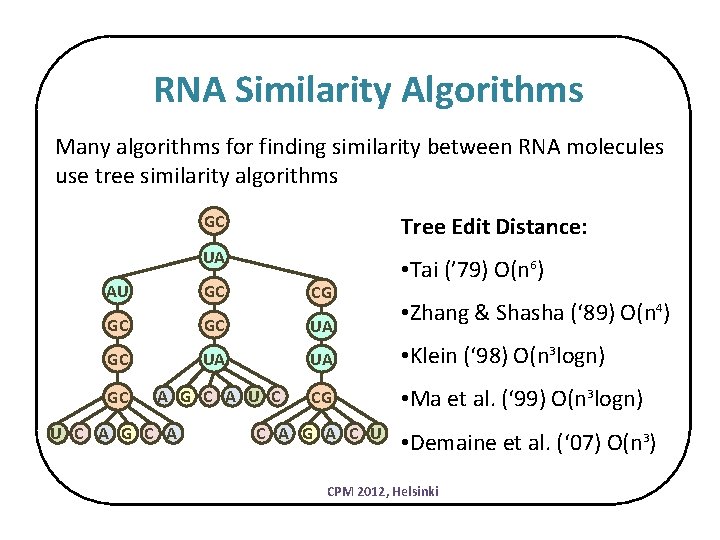
RNA Similarity Algorithms Many algorithms for finding similarity between RNA molecules use tree similarity algorithms GC Tree Edit Distance: UA • Tai (’ 79) O(n 6) AU GC CG GC GC UA UA • Klein (‘ 98) O(n 3 logn) GC A G C A U C CG • Ma et al. (‘ 99) O(n 3 logn) U C A G A C U • Zhang & Shasha (‘ 89) O(n 4) • Demaine et al. (‘ 07) O(n 3) CPM 2012, Helsinki

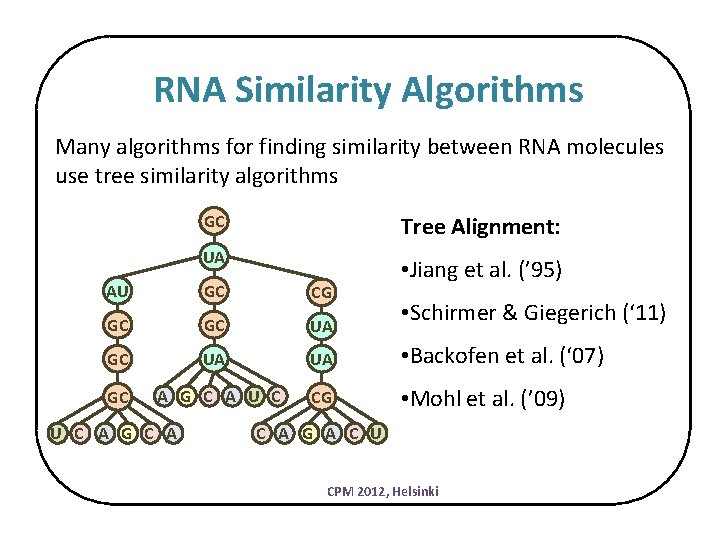
RNA Similarity Algorithms Many algorithms for finding similarity between RNA molecules use tree similarity algorithms GC Tree Alignment: UA • Jiang et al. (’ 95) AU GC CG GC GC UA UA • Backofen et al. (‘ 07) GC A G C A U C CG • Mohl et al. (’ 09) U C A G C A • Schirmer & Giegerich (‘ 11) C A G A C U CPM 2012, Helsinki

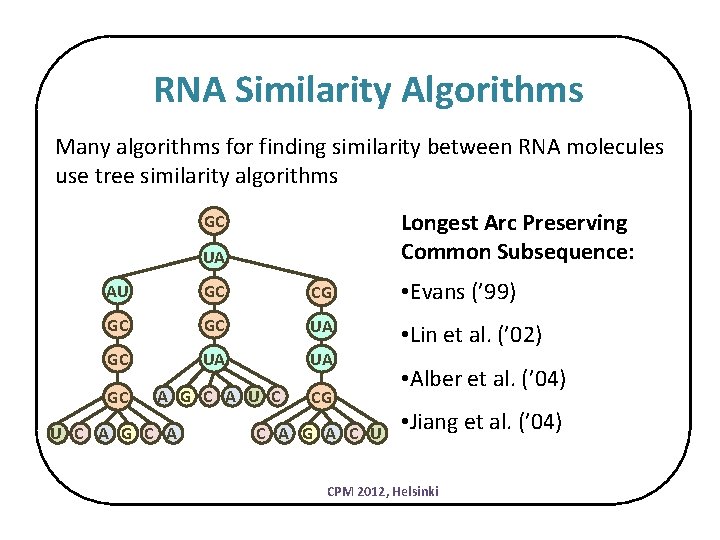
RNA Similarity Algorithms Many algorithms for finding similarity between RNA molecules use tree similarity algorithms Longest Arc Preserving Common Subsequence: GC UA AU GC CG • Evans (’ 99) GC GC UA UA • Lin et al. (’ 02) GC A G C A U C CG U C A G A C U • Alber et al. (’ 04) • Jiang et al. (’ 04) CPM 2012, Helsinki

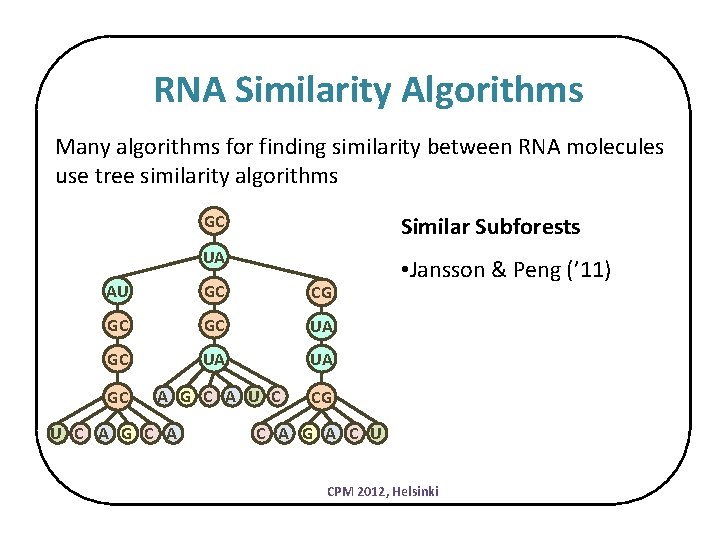
RNA Similarity Algorithms Many algorithms for finding similarity between RNA molecules use tree similarity algorithms GC Similar Subforests UA • Jansson & Peng (’ 11) AU GC CG GC GC UA UA GC A G C A U C CG U C A G A C U CPM 2012, Helsinki

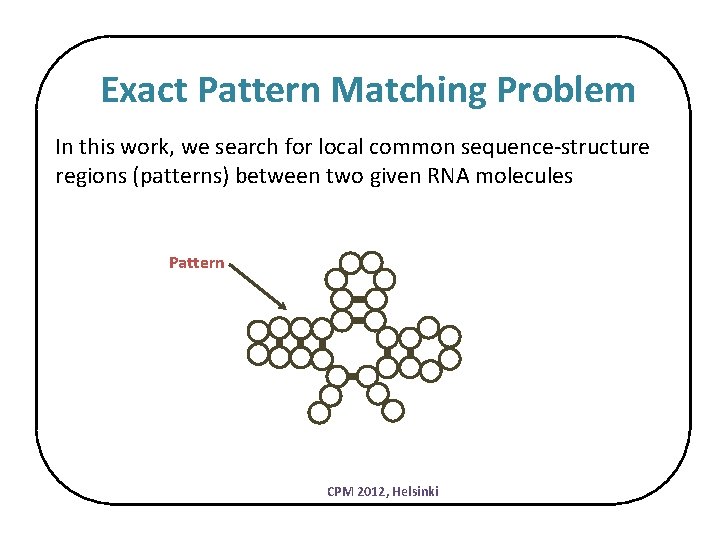
Exact Pattern Matching Problem In this work, we search for local common sequence-structure regions (patterns) between two given RNA molecules Pattern CPM 2012, Helsinki

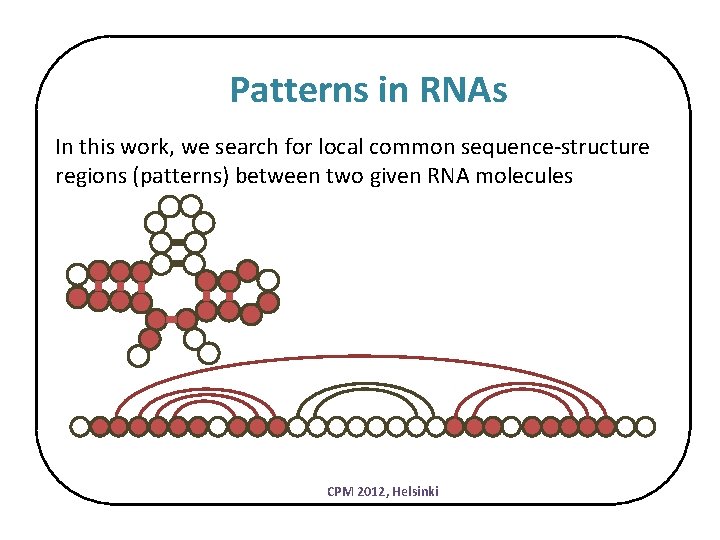
Patterns in RNAs In this work, we search for local common sequence-structure regions (patterns) between two given RNA molecules CPM 2012, Helsinki

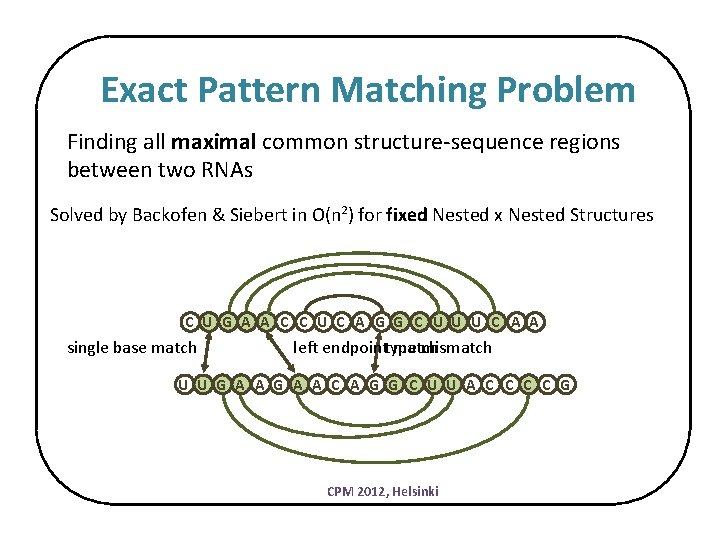
Exact Pattern Matching Problem Finding all maximal common structure-sequence regions between two RNAs Solved by Backofen & Siebert in O(n 2) for fixed Nested x Nested Structures C U G A A C C U C A G G C U U U C A A single base match left endpointtype match mismatch U U G A A C A G G C U U A C C G CPM 2012, Helsinki

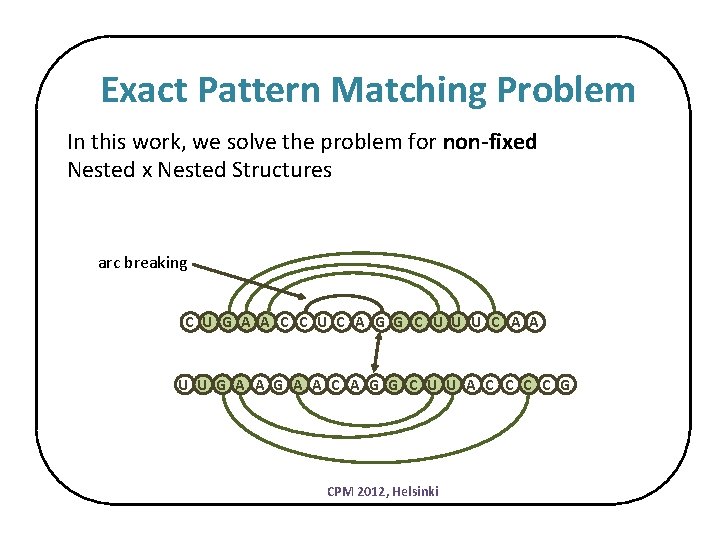
Exact Pattern Matching Problem In this work, we solve the problem for non-fixed Nested x Nested Structures arc breaking C U G A A C C U C A G G C U U U C A A U U G A A C A G G C U U A C C G CPM 2012, Helsinki

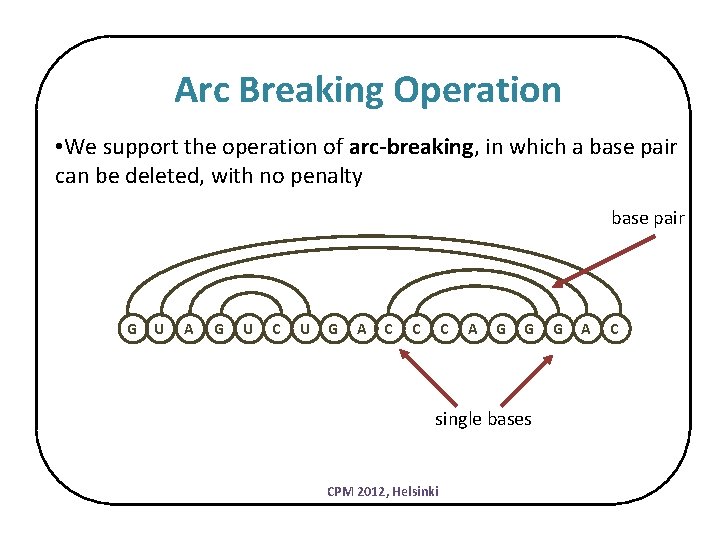
Arc Breaking Operation • We support the operation of arc-breaking, in which a base pair can be deleted, with no penalty base pair G U A G U C U G A C C C A G G single bases CPM 2012, Helsinki G A C

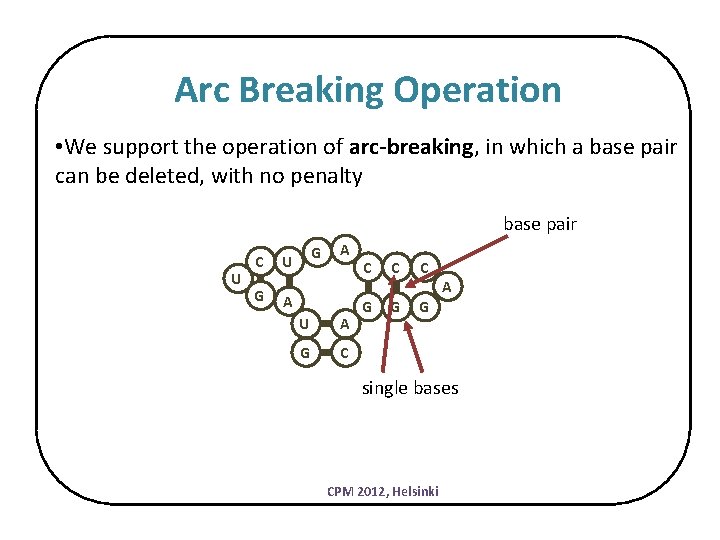
Arc Breaking Operation • We support the operation of arc-breaking, in which a base pair can be deleted, with no penalty base pair U C G G U A A U A G C C G G G A single bases CPM 2012, Helsinki

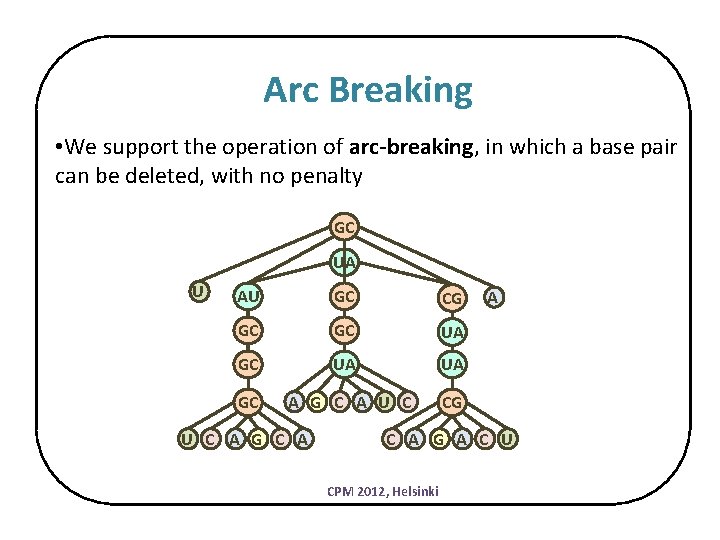
Arc Breaking • We support the operation of arc-breaking, in which a base pair can be deleted, with no penalty GC UA U AU GC CG GC GC UA UA GC A G C A U C CG U C A G C A A C A G A C U CPM 2012, Helsinki

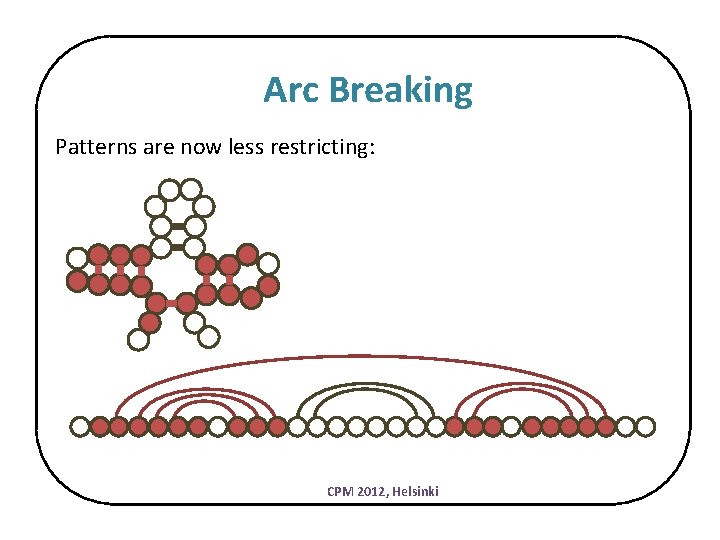
Arc Breaking Patterns are now less restricting: CPM 2012, Helsinki

Exact Pattern Matching Algorithms We describe three algorithms for finding the local exact pattern matching between two RNAs: • A simple O(n 4) algorithm (using ideas from Zhang & Shasha (‘ 89) ) • An improved O(n 3 logn) algorithm (using ideas from Klein (‘ 98) ) • An O(n 3) algorithm (using ideas from Demaine, Weimann et al. (‘ 07) ) CPM 2012, Helsinki

Exact Pattern Matching Algorithm Input: R 1=(S 1, B 1) and R 2=(S 2, B 2), |R 1|=n, |R 2|=m, n>m Output: Local exact pattern matching between R 1 and R 2 R 1: R 2: CPM 2012, Helsinki

Exact Pattern Matching Algorithm We compare each base pair from R 1 with each base pair from R 2, in increasing order of their sizes R 1: R 2: CPM 2012, Helsinki

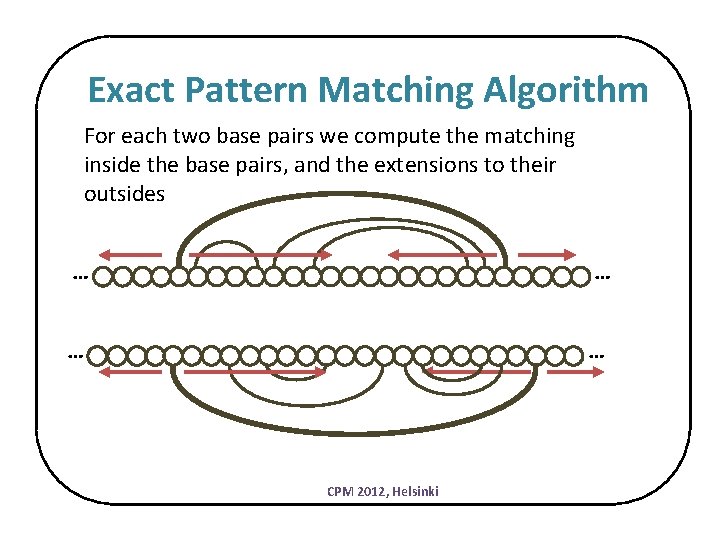
Exact Pattern Matching Algorithm For each two base pairs we compute the matching inside the base pairs, and the extensions to their outsides … … CPM 2012, Helsinki

Matching Inside the Base Pairs • Dynamic programming algorithm • Similar to the LCSEdit distance algorithms of strings CPM 2012, Helsinki

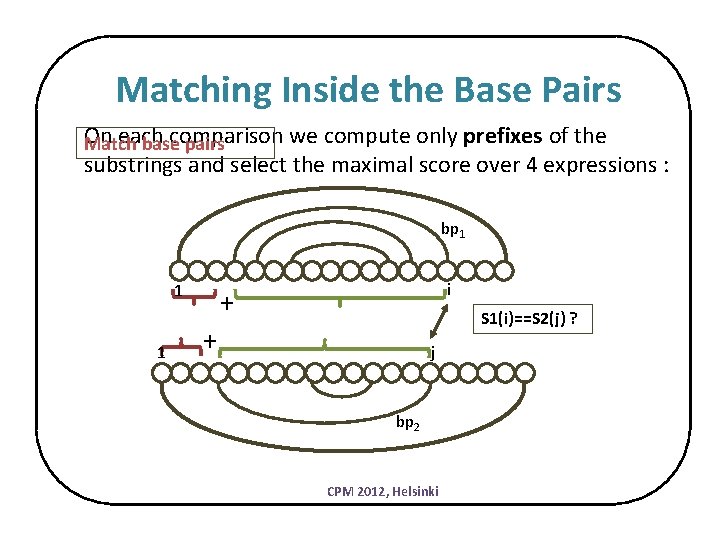
Matching Inside the Base Pairs On each comparison we compute only prefixes of the Match base pairs substrings and select the maximal score over 4 expressions : bp 1 1 1 i + S 1(i)==S 2(j) ? + j bp 2 CPM 2012, Helsinki

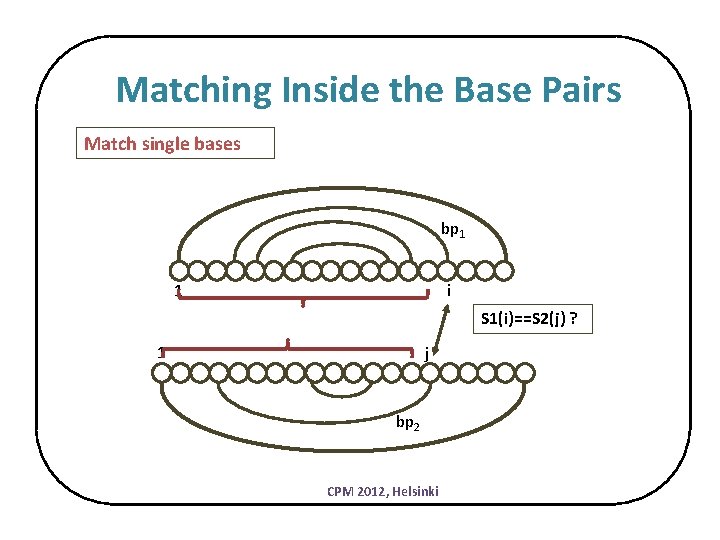
Matching Inside the Base Pairs Match single bases bp 1 1 i S 1(i)==S 2(j) ? 1 j bp 2 CPM 2012, Helsinki

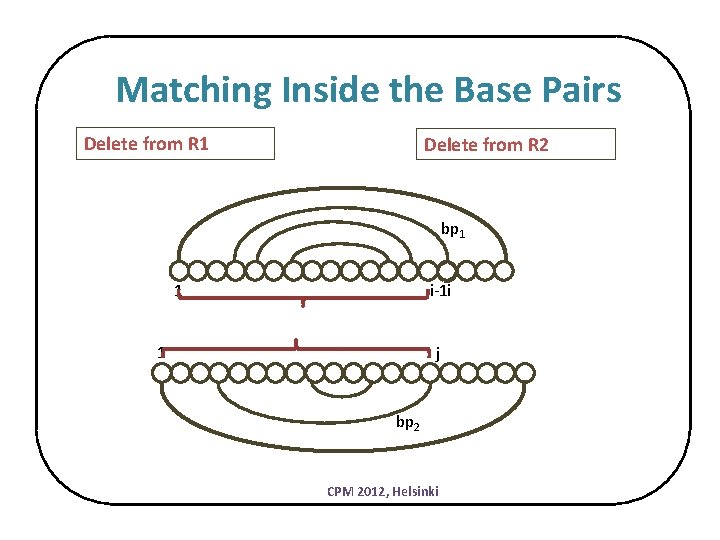
Matching Inside the Base Pairs Delete from R 1 Delete from R 2 bp 1 1 i-1 i 1 j bp 2 CPM 2012, Helsinki

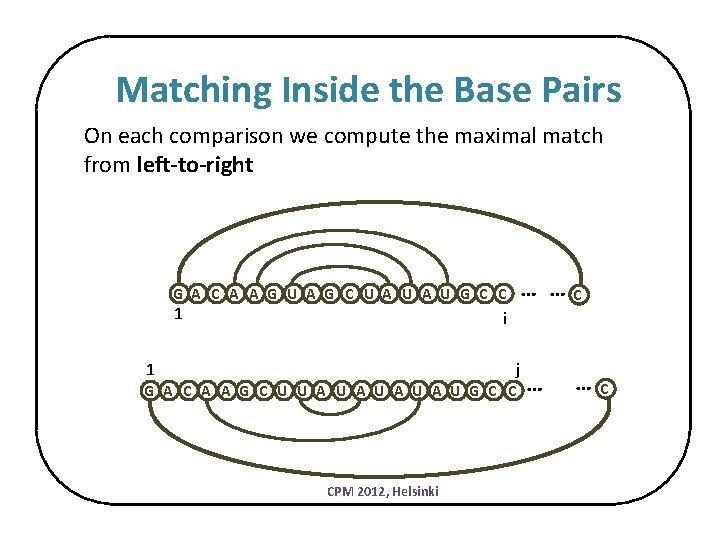
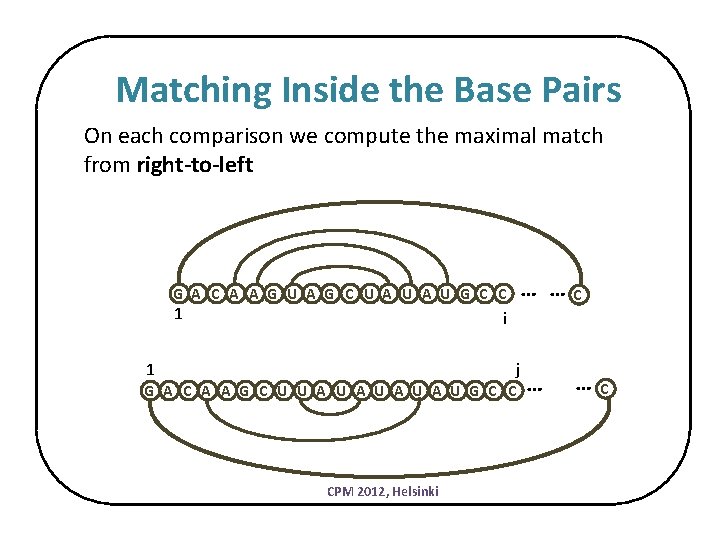
Matching Inside the Base Pairs On each comparison we compute the maximal match from left-to-right … … G A C A A G U A G C U A U G C C 1 C i j 1 G A C A A G C U U A U A U G C C CPM 2012, Helsinki … … C

Matching Inside the Base Pairs On each comparison we compute the maximal match from right-to-left … … G A C A A G U A G C U A U G C C 1 C i j 1 G A C A A G C U U A U A U G C C CPM 2012, Helsinki … … C

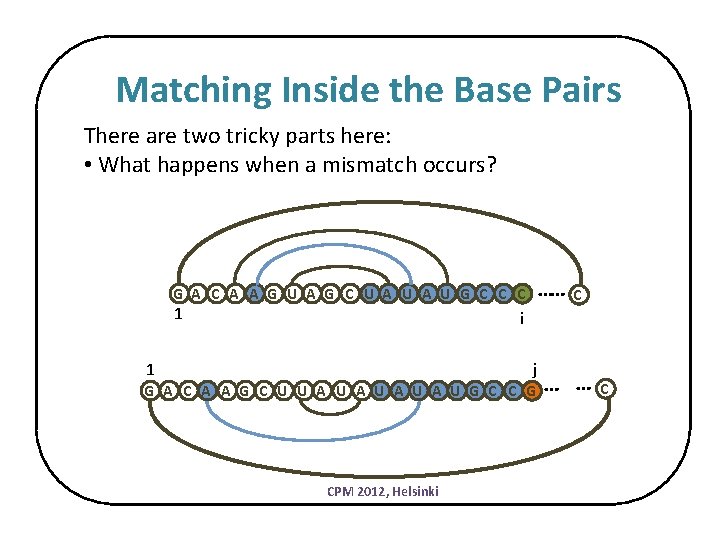
Matching Inside the Base Pairs There are two tricky parts here: • What happens when a mismatch occurs? …… G A C A A G U A G C U A U G C C C 1 C i j 1 G A C A A G C U U A U A U G C C G CPM 2012, Helsinki … … C

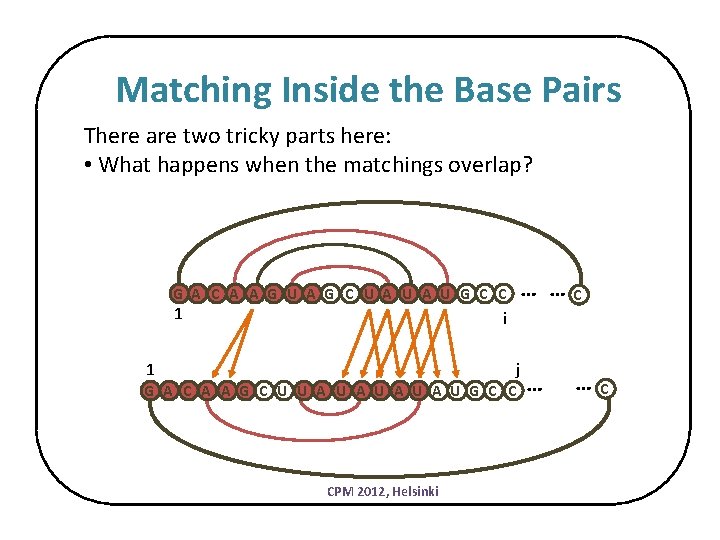
Matching Inside the Base Pairs There are two tricky parts here: • What happens when the matchings overlap? … … G A C A A G U A G C U A U G C C 1 C i j 1 G A C A A G C U U A U A U G C C CPM 2012, Helsinki … … C

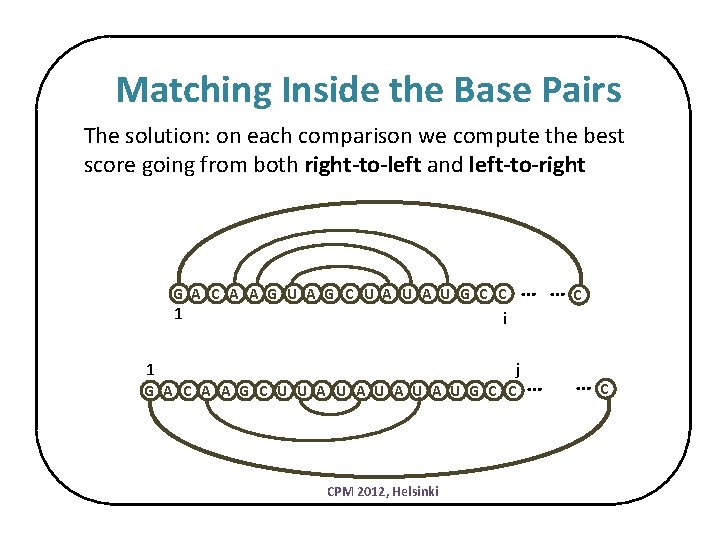
Matching Inside the Base Pairs The solution: on each comparison we compute the best score going from both right-to-left and left-to-right … … G A C A A G U A G C U A U G C C 1 C i j 1 G A C A A G C U U A U A U G C C CPM 2012, Helsinki … … C

Time Complexity • We only compare prefixes of the base pairs • There are O(n 2) prefixes for each RNA • Each comparison is computed in O(1) time • The total time is O(n 4) CPM 2012, Helsinki

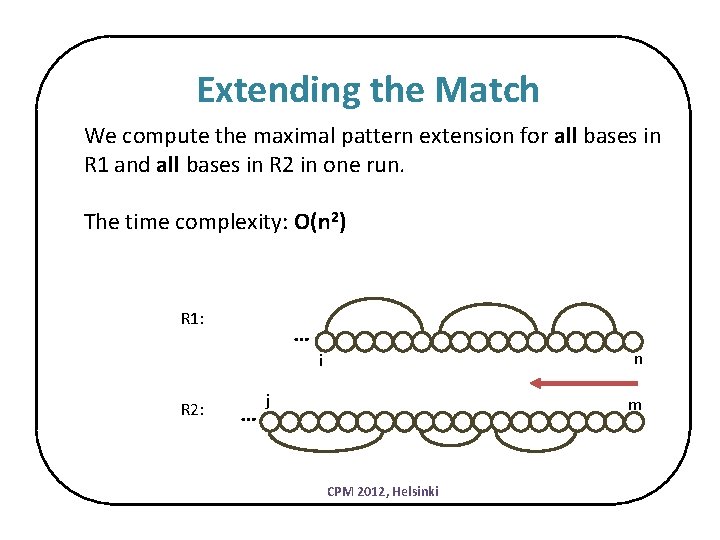
Extending the Match We compute the maximal pattern extension for all bases in R 1 and all bases in R 2 in one run. The time complexity: O(n 2) R 1: … n i R 2: … j m CPM 2012, Helsinki

Total Time Complexity Computing the pattern match inside all base pairs is done in O(n 4) + Computing the pattern match extensions to the right and to the left is done in O(n 2) = The total time complexity is O(n 4) CPM 2012, Helsinki

An O(n logn) Algorithm 3 We use Klein’s Tree Edit Distance (‘ 98) ideas: we decompose the largest RNA into heavy paths: The root base pair is marked light, and continue recursively: Select the maximal child base pair and mark it as heavy, mark the rest of the children as light C C G A A U C C G A G U U C G G G U C C C A G G CPM 2012, Helsinki

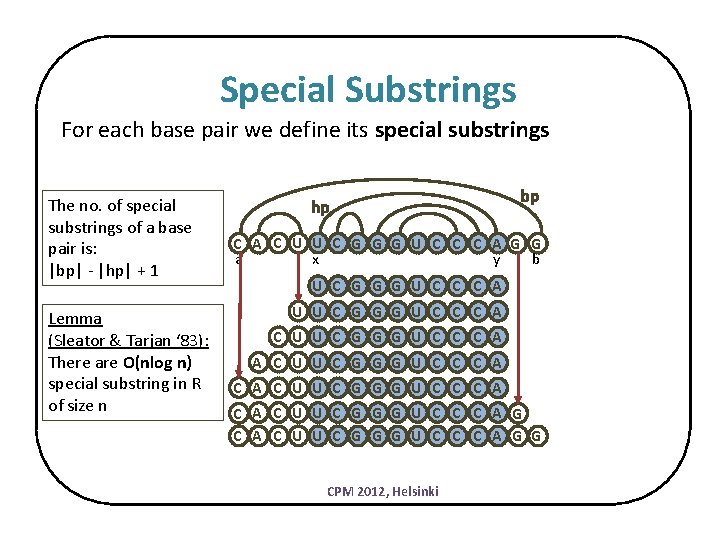
Special Substrings For each base pair we define its special substrings The no. of special substrings of a base pair is: |bp| - |hp| + 1 Lemma (Sleator & Tarjan ‘ 83): There are O(nlog n) special substring in R of size n hp bp C A C U U C G G G U C C C A G G a x y b U C G G G U C C C A U U C G G G U C C C A C A C U U C G G G U C C C A G C A C U U C G G G U C C C A G G CPM 2012, Helsinki

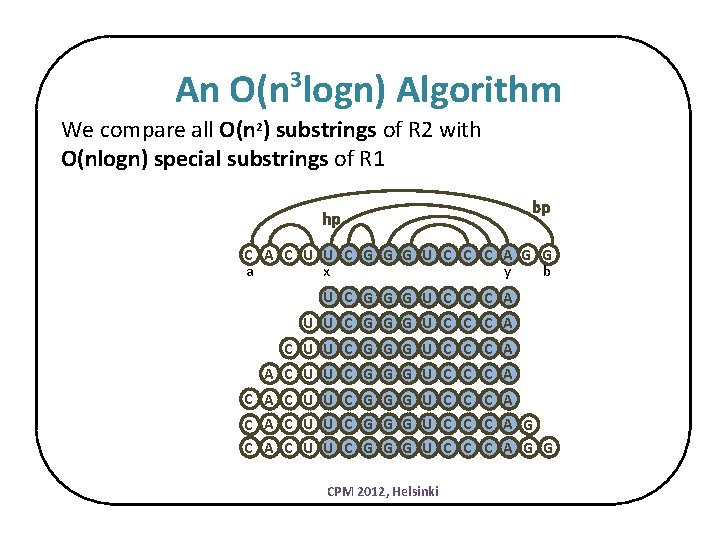
An O(n logn) Algorithm 3 We compare all O(n 2) substrings of R 2 with O(nlogn) special substrings of R 1 hp bp C A C U U C G G G U C C C A G G a x y b U C G G G U C C C A U U C G G G U C C C A C A C U U C G G G U C C C A G C A C U U C G G G U C C C A G G CPM 2012, Helsinki

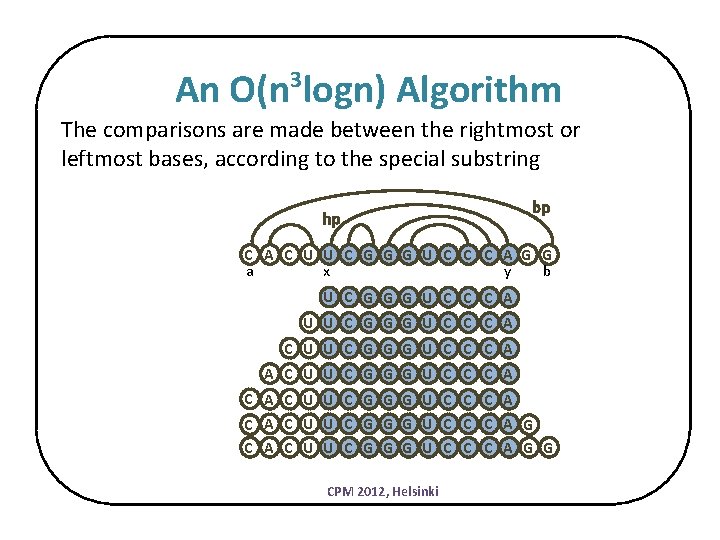
An O(n logn) Algorithm 3 The comparisons are made between the rightmost or leftmost bases, according to the special substring hp bp C A C U U C G G G U C C C A G G a x y b U C G G G U C C C A U U C G G G U C C C A C A C U U C G G G U C C C A G C A C U U C G G G U C C C A G G CPM 2012, Helsinki

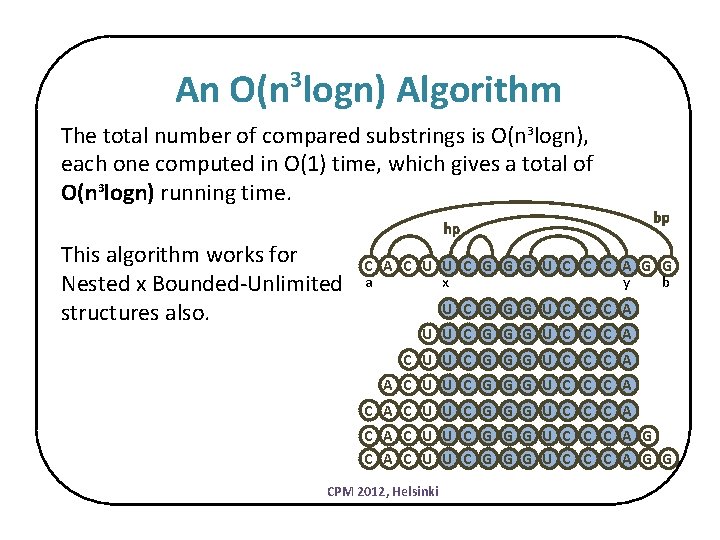
An O(n logn) Algorithm 3 The total number of compared substrings is O(n 3 logn), each one computed in O(1) time, which gives a total of O(n 3 logn) running time. hp This algorithm works for Nested x Bounded-Unlimited structures also. bp C A C U U C G G G U C C C A G G a x y b U C G G G U C C C A U U C G G G U C C C A C A C U U C G G G U C C C A G C A C U U C G G G U C C C A G G CPM 2012, Helsinki

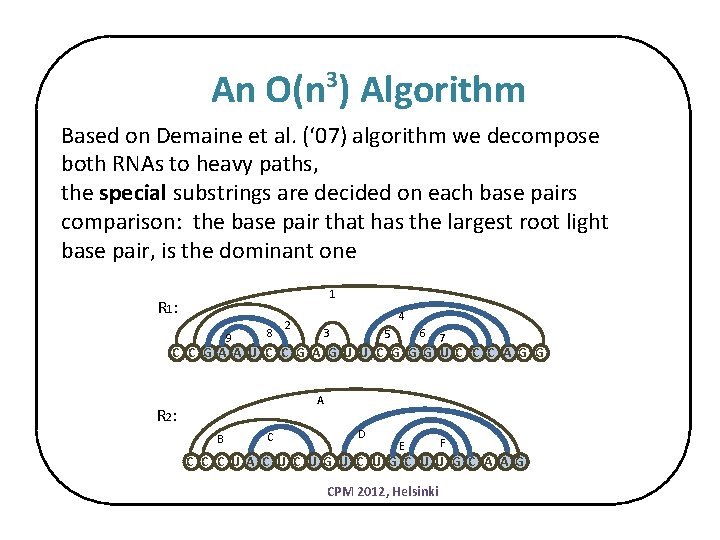
An O(n ) Algorithm 3 Based on Demaine et al. (‘ 07) algorithm we decompose both RNAs to heavy paths, the special substrings are decided on each base pairs comparison: the base pair that has the largest root light base pair, is the dominant one 1 R 1 : 9 8 4 2 3 6 5 7 C C G A A U C C G A G U U C G G G U C C C A G G A R 2 : B C D E F C C C U A C U G U C U G C U U G C A A G CPM 2012, Helsinki

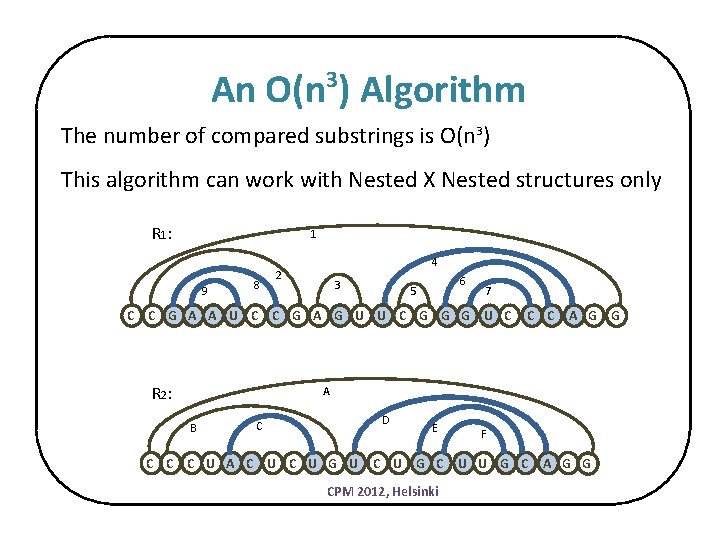
An O(n ) Algorithm 3 The number of compared substrings is O(n 3) This algorithm can work with Nested X Nested structures only R 1 : 1 9 8 4 2 3 6 5 7 C C G A A U C C G A G U U C G G G U C R 2 : C C A G G A B D C C U A C U G U E C U G C CPM 2012, Helsinki F U U G C A G G

More Algorithms • Find the local approximate pattern matching between Nested x Nested structures in O(n 3 k 2) for k allowed mismatches • Find the local approximate pattern matching between Nested x Bounded-Unlimited structures in O(n 3 k 2 logn) for k allowed mismatches • Find the most similar sibling substructures between Nested x Nested structures in O(n 3) CPM 2012, Helsinki

T H A N K Y O U !