Loai Tawalbeh Lecture 2 Standard combinational modules decoders

Lo’ai Tawalbeh Lecture #2 Standard combinational modules: decoders, encoders and Multiplexers 1/3/2005 cpe 252: Computer Organization 1
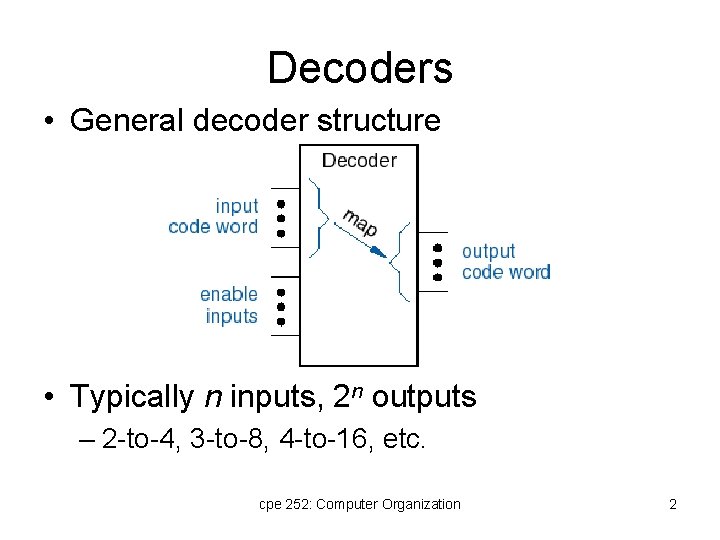
Decoders • General decoder structure • Typically n inputs, 2 n outputs – 2 -to-4, 3 -to-8, 4 -to-16, etc. cpe 252: Computer Organization 2

Binary 2 -to-4 decoder Note: “x” = (don’t care) cases. cpe 252: Computer Organization 3
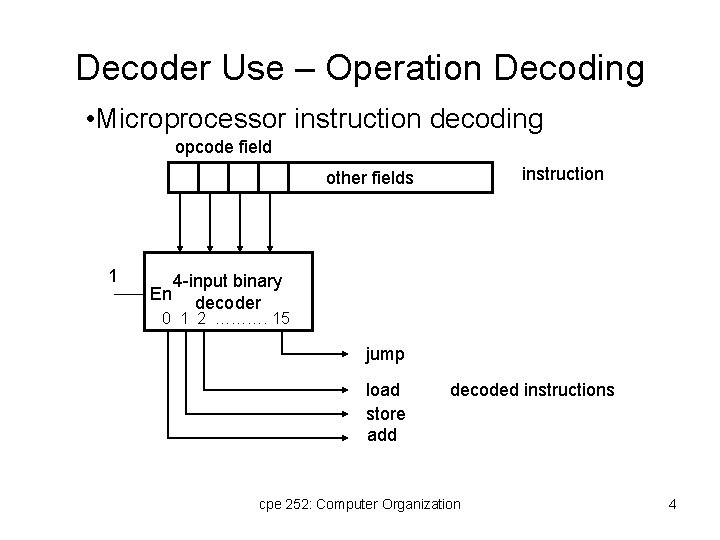
Decoder Use – Operation Decoding • Microprocessor instruction decoding opcode field instruction other fields 1 En 4 -input binary decoder 0 1 2 ………. 15 jump load store add decoded instructions cpe 252: Computer Organization 4
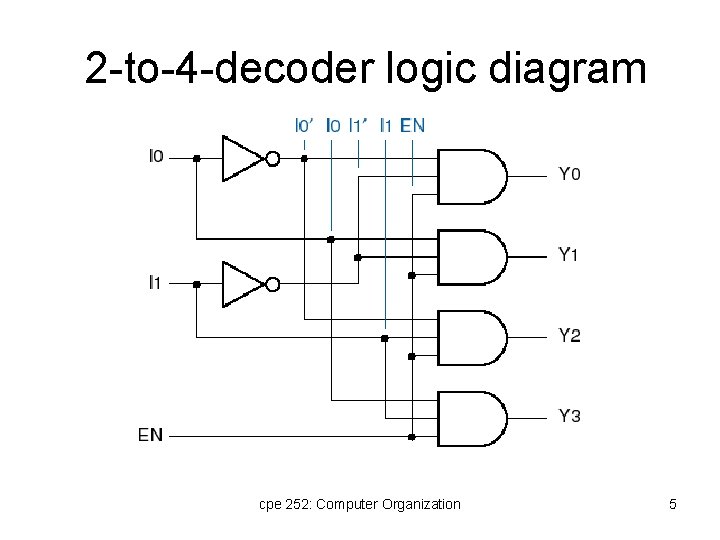
2 -to-4 -decoder logic diagram cpe 252: Computer Organization 5

3 -input Binary Decoder E 1 1 1 1 0 x 2 0 0 1 1 - x 1 0 0 1 1 - x 0 0 1 0 1 - x 0 1 2 3 4 5 6 7 - y 7 0 0 0 0 1 0 y 6 0 0 0 1 0 0 y 5 0 0 0 1 0 0 0 y 4 0 0 1 0 0 y 3 0 0 0 1 0 0 0 y 2 0 0 1 0 0 0 y 1 0 0 0 0 y 0 1 0 0 0 0 Inputs: x = (x 2, x 1, x 0), with xi in {0, 1} and E in {0, 1} Outputs: y = (y 7, y 6, y 5, …, y 1, y 0) with yi in {0, 1} Function: yi = E. mi(x), i = 0, 1, …, 7 cpe 252: Computer Organization 6
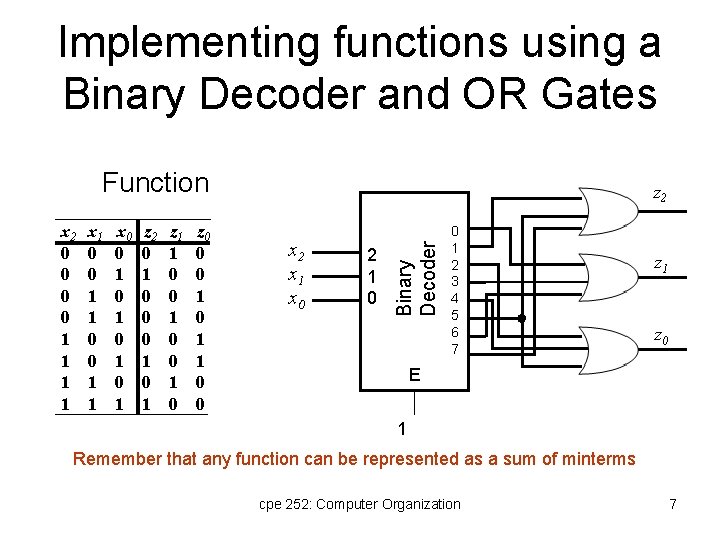
Implementing functions using a Binary Decoder and OR Gates Function x 1 0 0 1 1 x 0 0 1 0 1 z 2 0 1 0 0 0 1 z 1 1 0 0 1 0 z 0 0 0 1 1 0 0 x 2 x 1 x 0 2 1 0 Binary Decoder x 2 0 0 1 1 z 2 0 1 2 3 4 5 6 7 z 1 z 0 E 1 Remember that any function can be represented as a sum of minterms cpe 252: Computer Organization 7
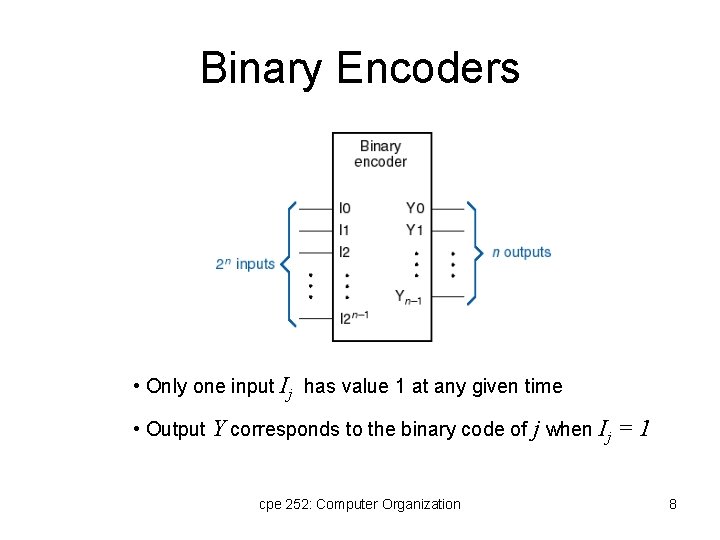
Binary Encoders • Only one input Ij has value 1 at any given time • Output Y corresponds to the binary code of j when Ij = 1 cpe 252: Computer Organization 8
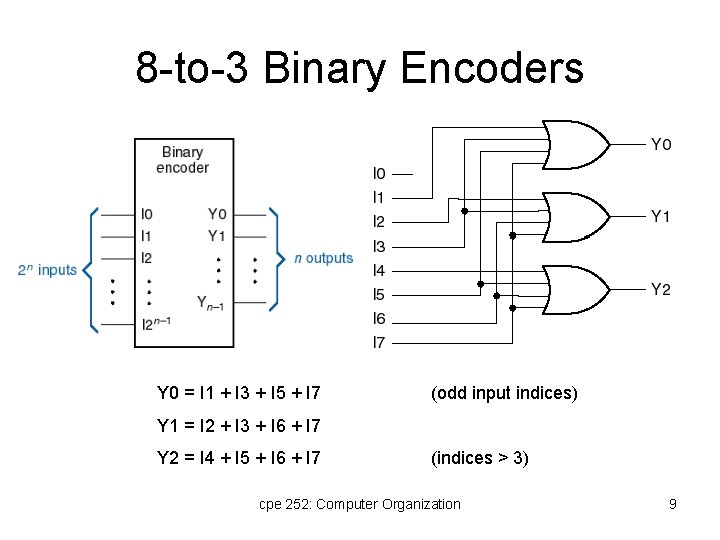
8 -to-3 Binary Encoders Y 0 = I 1 + I 3 + I 5 + I 7 (odd input indices) Y 1 = I 2 + I 3 + I 6 + I 7 Y 2 = I 4 + I 5 + I 6 + I 7 (indices > 3) cpe 252: Computer Organization 9
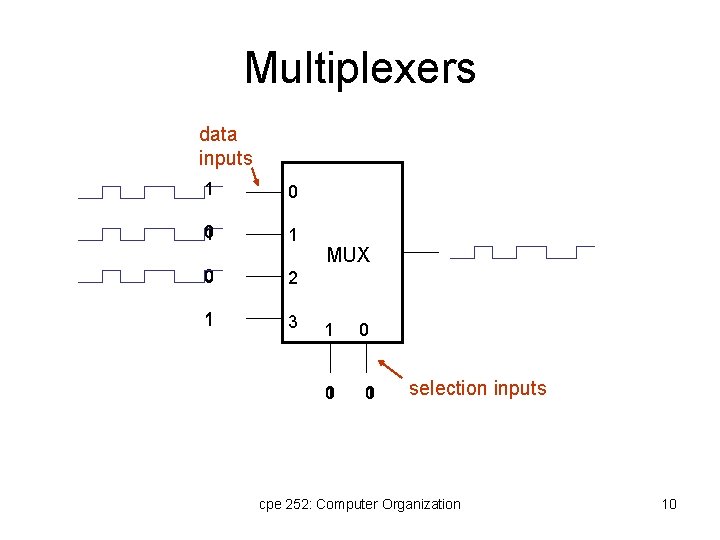
Multiplexers data inputs 1 0 0 1 1 0 2 1 3 MUX 1 0 1 0 selection inputs cpe 252: Computer Organization 10
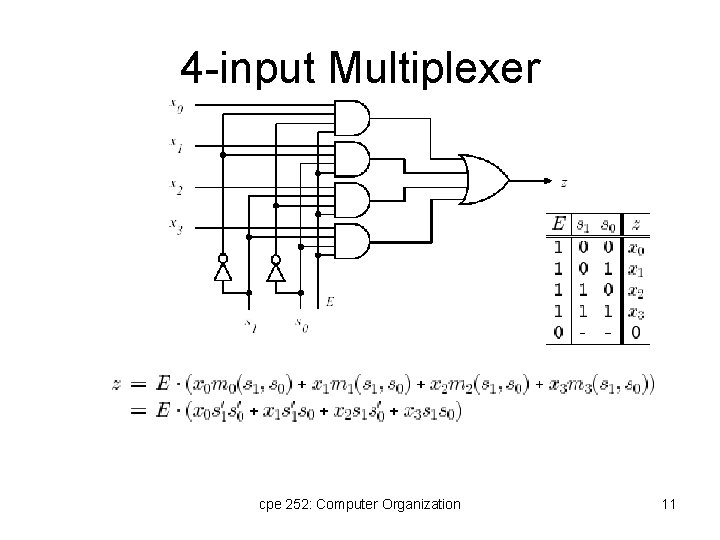
4 -input Multiplexer cpe 252: Computer Organization 11
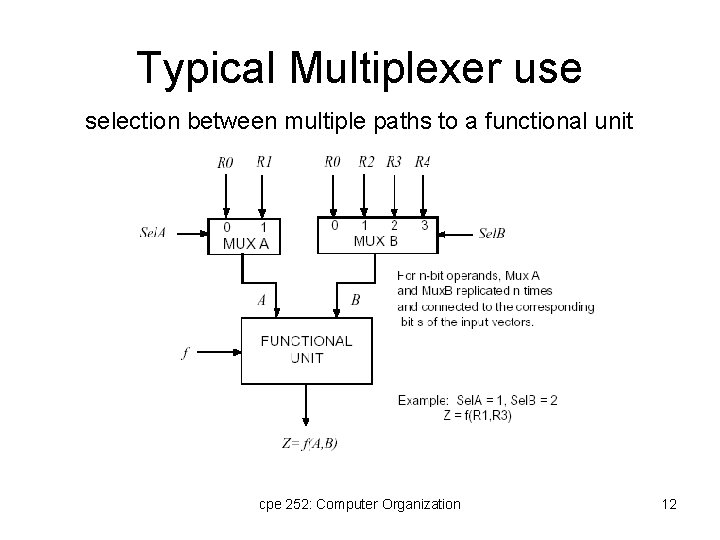
Typical Multiplexer use selection between multiple paths to a functional unit cpe 252: Computer Organization 12

Multiplexers as universal modules • Universal module: using only this module you are able to implement ANY logic function. • NAND and NOR gates for example are universal gates. • Question: how do you assign inputs for the multiplexer in order to implement a given function? cpe 252: Computer Organization 13

Exercise Implement the following function using: a) 8 -input multiplexer. b) 4 -input multiplexer. F= x, y, z(1, 2, 6, 7) cpe 252: Computer Organization 14

Lo’ai Tawalbeh Lecture #2 Signed and Unsigned Numbers cpe 252: Computer Organization 15
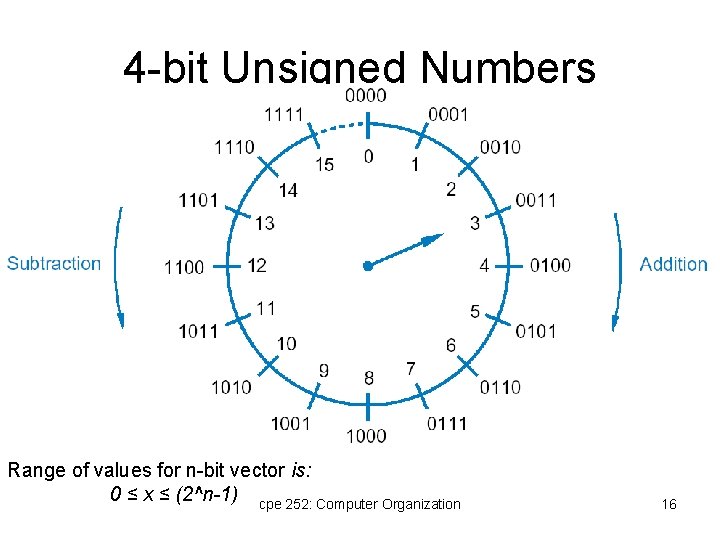
4 -bit Unsigned Numbers Range of values for n-bit vector is: 0 ≤ x ≤ (2^n-1) cpe 252: Computer Organization 16

Representation of Signed Integers and Basic Operations • Two common representations – Sign and Magnitude (SM) – True and Complement (TC) • In both cases there is a mapping from signed values to positive values. cpe 252: Computer Organization 17

Sign and Magnitude • x represented by a pair (s, m) where – s is the sign: 0 for positive and 1 for negative – m is the magnitude – example: (-23)10 = -(10111) = (1, 10111) • Range of values for n-bit vector (n-1 bits for m) – - (2 n-1 – 1) ≤ x ≤ (2 n-1 – 1) cpe 252: Computer Organization • Two representations for zero 18

2’s complement • No separation between sign and magnitude • Signed integer x represented by positive integer x. R such that: Example: n=4, 2^4=16. To represent x = -7; x. R = 9 • Range of values for n-bit vector ( 2’s comlement) – - (2 n-1 ) ≤ x ≤ (2 n-1 – 1) cpe 252: Computer Organization 19
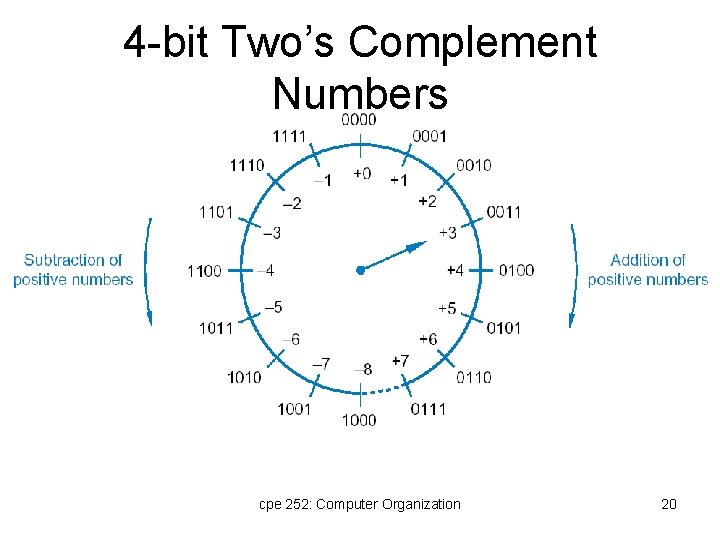
4 -bit Two’s Complement Numbers cpe 252: Computer Organization 20

Change of Sign 1. complement each bit of x 2. add 1 Example: n = 4 x’ = x = (0011)2= 3 1100 +1 1101 representation of -3 cpe 252: Computer Organization 21
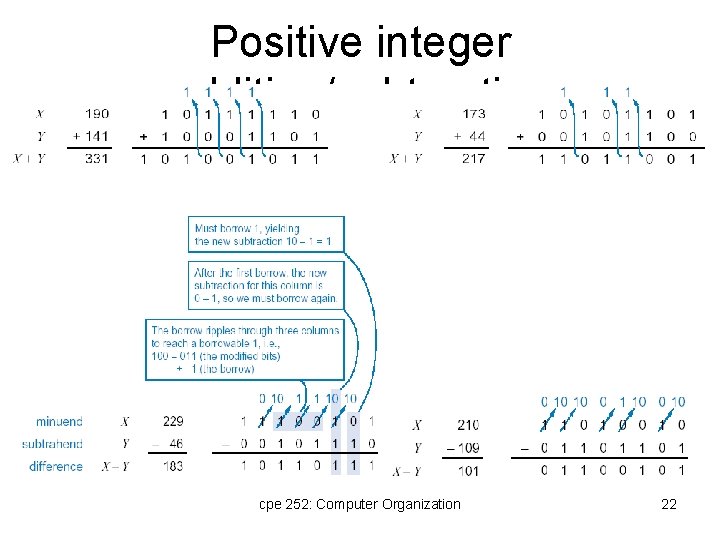
Positive integer addition/subtraction cpe 252: Computer Organization 22

Two’s complement addition/subtraction • Addition: same as positive integer addition – just discard carry out • Subtraction: x - y – step 1: change the sign of y to obtain -y – step 2: add x and -y • Example: x = 8, y = 5, 5 -bit vectors y = 00101 -y = 11011 <<< change sign x - y = 01000 11011 + 00011 << carry out discarded cpe 252: Computer Organization 23
- Slides: 23