Load Balancing in Heterogeneous Processors Omar Darwish Definition

Load Balancing in Heterogeneous Processors Omar Darwish

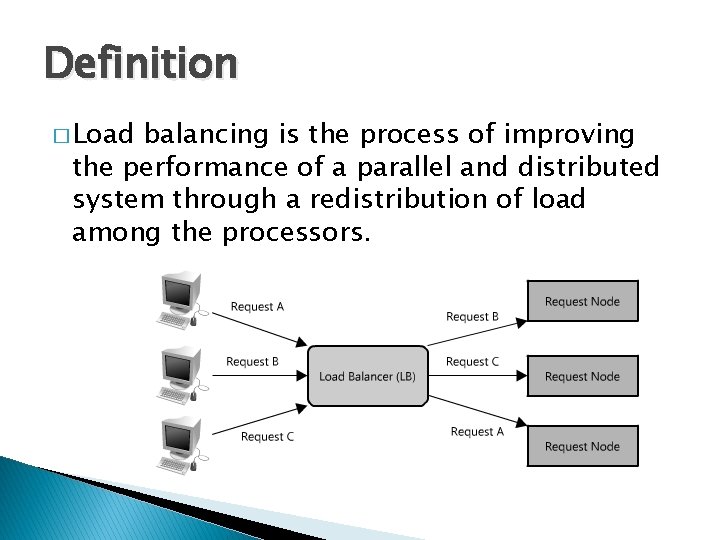
Definition � Load balancing is the process of improving the performance of a parallel and distributed system through a redistribution of load among the processors.

Types of Load Balancing Algorithms Who Initialized the load balancing algorithm ? � Sender Initiated ◦ Initialized by the sender. ◦ Sender sends request messages till it finds a receiver that can accept the load. � Receiver Initiated ◦ Initiated by the receiver. ◦ Receiver sends request messages till it finds a sender that can get the load.

Static Load Balancing � The performance of the processors is determined at the beginning of execution. � Master �A processor and slave processors. task is always executed on the processor to which it is assigned. � Reduce the execution time, minimizing the communication delays

Static Algorithms � Round Robin Algorithm ◦ Processor choosing is performed in series and will be back to the first processor if the last processor has been reached. � Randomized Algorithm ◦ Uses random numbers to choose slave processors based on statistics.

Static Algorithms Cont… � Central Manager Algorithm ◦ The central processor is able to gather all slave processors load information ◦ The chosen slave processor is the processor having the least load � Threshold Algorithm ◦ The processes are assigned immediately upon creation to hosts. ◦ Under loaded, medium and overloaded.

Dynamic Load Balancing � Dynamic algorithms allocate processes dynamically when one of the processors becomes under loaded. � Buffered in the queue � Allocated dynamically upon requests from remote hosts

Dynamic Load Balancing Algorithms � Central Queue ◦ Stores new activities and unfulfilled requests as a cyclic FIFO queue on the main host. � Local �A Queue parameter defines the minimal number of ready processes the load manager attempts to provide on each processor

Performance Analysis of Load Balancing Algorithms � Adaptability ◦ Static No, Dynamic Yes � Predictability ◦ Static Yes, Dynamic No � Waiting Time (Queuing time ) � Execution System

Load Balancing in Distributed System using Genetic Algorithm � Fitness Function ◦ The main objective of GA is to find a schedule with optimal cost while load-balancing. �Less execution time. �Less communication cost. �Higher processor utilization. �Maximum system throughput

Cont… � Selection �Processors permutation � Crossover �Exchange portions between strings. � Mutation � Change the genes in a chromosome (Processors set)

Optimal solution for Task allocation problem � NP complete problem. � Untractable with large N of tasks and P number of processors.

Model description Actual execution cost If we consider communication time, the work load L is

Cont… � Objective function

Weighted Round Robin

Example : � Processor 1 3 tasks/slot � Processor 2 6 tasks/slot � GCD =3 � P 1 P 0 P 1 GCD in parallel O(n log n/log n),

Fibonacci & Linear Algorithms � Static Algorithms � Round robin fashion � Heterogeneous � Weighting � Fibonacci processors depends on capabilities gives the high capabilities processors extra load.

Psedocode � Rank processors depends on capabilities � Give each processor weight depends on its rank (linearly or Fibonacci) � While (process<>0) ◦ Assign tasks for each processor depends on its weight

Example � Linear � Ex ◦ ◦ ◦ approach Ordering weights (1, 2…, 7) 7 processors The highest capability takes weight 7 The lowest capability takes weight 1 Processor 7 will get 7 process each slot time Processor 1 will get 1 process each slot time

Example � Fibonacci � Ex ◦ ◦ approach Ordering weights (1, 1, 2, 3, 5, 8, 13) 7 processors The highest capability takes weight 13 The lowest capability takes weight 1 � Processor 7 will get 13 process each slot time � Processor 1 will get 1 process each slot time

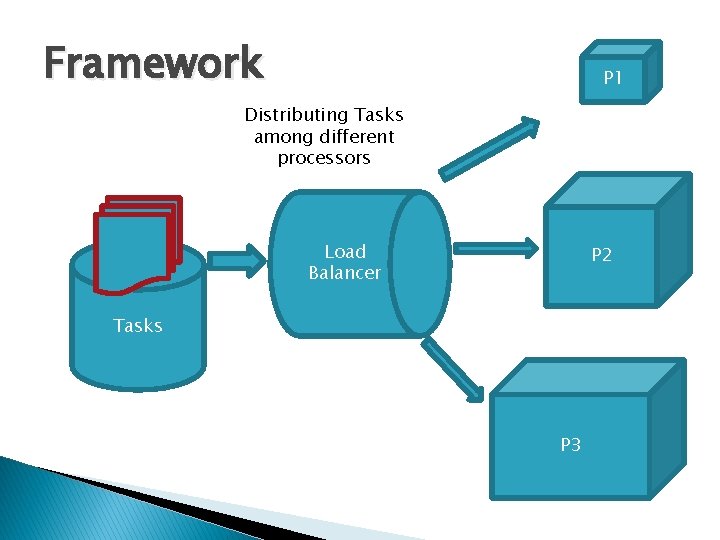
Framework P 1 Distributing Tasks among different processors Load Balancer P 2 Tasks P 3

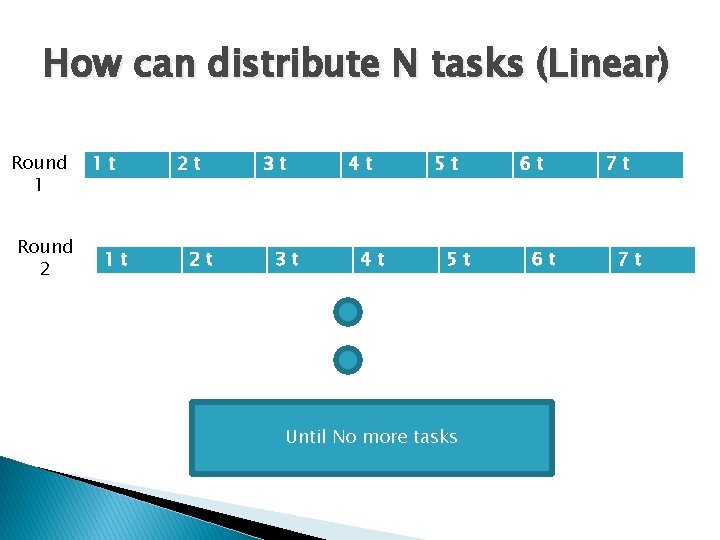
How can distribute N tasks (Linear) Round 1 Round 2 1 t 1 t 2 t 2 t 3 t 3 t 4 t 4 t 5 t 5 t Until No more tasks 6 t 6 t 7 t 7 t

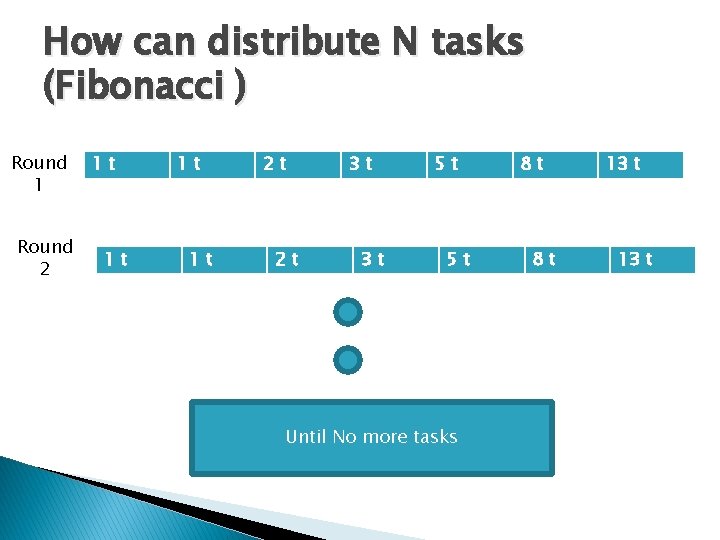
How can distribute N tasks (Fibonacci ) Round 1 Round 2 1 t 1 t 2 t 2 t 3 t 3 t 5 t 5 t Until No more tasks 8 t 8 t 13 t

System constraints �M tasks �K processors � How to distribute tasks among the processors � Less drops packets � Less time

Simulation Parameters � Number of processors N 6, 7, 8, 9, 10 � Processors speed : ◦ High speeds (N/2) =0. 10 * i i is the processor # ◦ Low speeds (N/2) =0. 03 * i i is the processor # �For example processor with id 6 can process 6. 0*0. 10*number of tasks in the Queue �Processor with id 2 can process 2. 0*0. 3*number of tasks in the Queue. � Memory For High speed computers 20 * i locations For low speed computers 320*i locations � 1000 tasks � Arrival packets =20, 33, ….

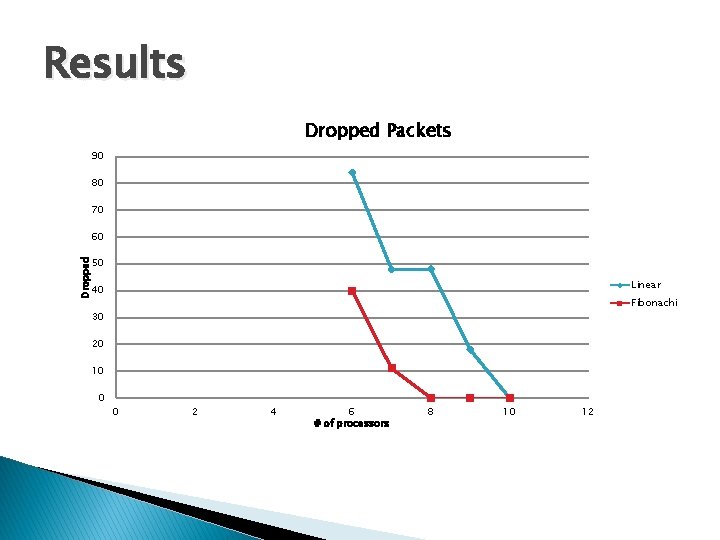
Results Dropped Packets 90 80 70 60 Dropped 50 Linear 40 Fibonachi 30 20 10 0 0 2 4 6 # of processors 8 10 12

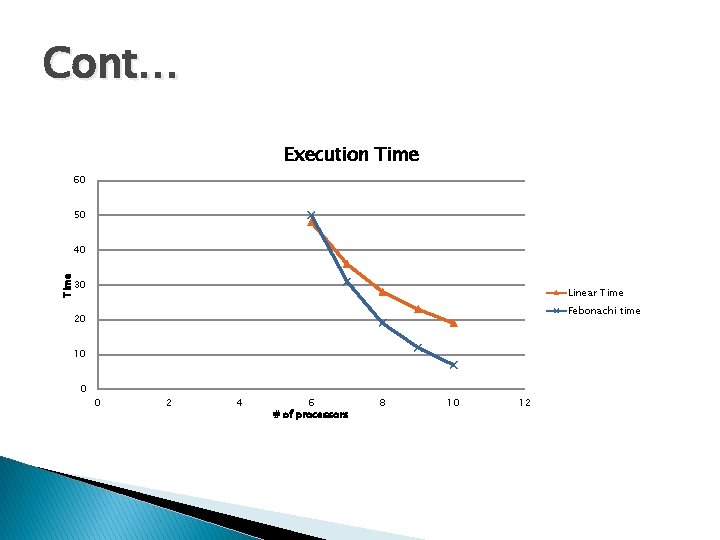
Cont… Execution Time 60 50 Time 40 30 Linear Time Febonachi time 20 10 0 0 2 4 6 # of processors 8 10 12

Cont… � Fibonacci distribution guarantee the more utilization of higher capabilities processors and less load on the less capabilities processors.

Conclusion � The presentation explore: ◦ Static vs. Dynamic load balancing technique. ◦ The formulization of task scheduling problem.

References � � � Sharma, Sandeep, Sarabjit Singh, and Meenakshi Sharma. "Performance analysis of load balancing algorithms. " World Academy of Science, Engineering and Technology 38 (2008): 269 -272. Rajguru, Abhijit A. , and S. S. Apte. "A Comparative Performance Analysis of Load Balancing Algorithms in Distributed System using Qualitative Parameters. " International Journal of Recent Technology and Engineering 1. 3 (2012). Shah, Purnima, and S. M. Shah. "Load Balancing in Distributed System Using Genetic Algorithm}. " Special issues on IP Multimedia Communications}: 139 -142. Attiya, Gamal, and Yskandar Hamam. "Task allocation for minimizing programs completion time in multicomputer systems. " Computational Science and Its Applications–ICCSA 2004. Springer Berlin Heidelberg, 2004. 97 -106. Chor, Benny, and Oded Goldreich. "An improved parallel algorithm for integer GCD. " Algorithmica 5. 1 -4 (1990): 1 -10. http: //kb. linuxvirtualserver. org/wiki/Weighted_Round-Robin_Scheduling

Questions ?