LLR Analysis Relativistic Model and Tests of Gravitational

LLR Analysis – Relativistic Model and Tests of Gravitational Physics James G. Williams Dale H. Boggs Slava G. Turyshev Jet Propulsion Laboratory California Institute of Technology, USA LLR Workshop, Boston, MA Dec 9 -10, 2010 Copyright 2010. All rights reserved.

Introduction • Lunar Laser Ranging (LLR) from 1970 -2010, from 4 Earth stations (Mc. Donald, Haleakala, OCA, Apache Point) to 5 retroreflector arrays, probes gravitational physics. • The lunar orbit is sensitive to: – – Equivalence principle. Geodetic precession. Change in the gravitational constant G. Change in scale. • Gravitational physics results depend on accurate models for data analysis.

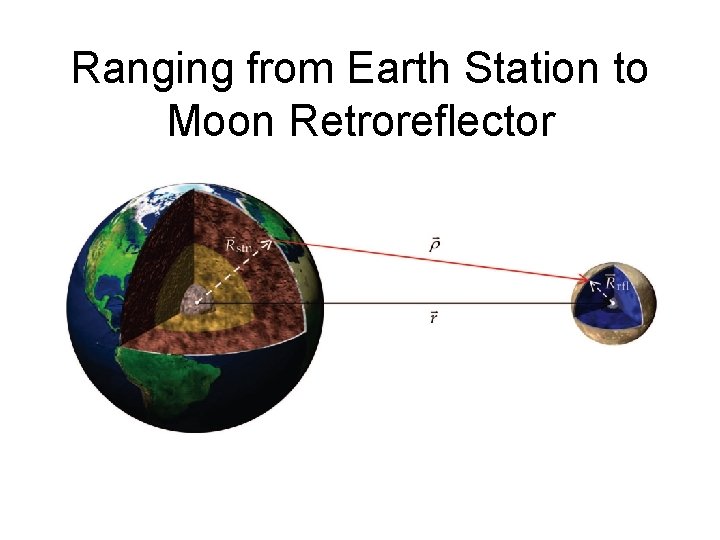
Lunar Laser Ranges • Laser pulses sent from stations on the Earth toward the Moon bounce off of retroreflector arrays and return to the Earth. • Ranging started in 1969 & continues to 2010.

Ranging from Earth Station to Moon Retroreflector

Retroreflector Arrays

Fit and Model • LLR range data is fit with a weighted leastsquares approach. • Observed time of flight from transmit to receive time (range) is compared with a computed time of flight. • Computed range depends on orbits and rotations of Earth & Moon, station & reflector positions, general relativity, tides on Earth & Moon, atmosphere, station motion, + other model effects.

Frames, Clocks, Computation– 1 • Observed time-of-flight “ranges” use clocks at stations to measure interval from transmit to receive times. Clocks are compared with broadcast UTC. • Numerically integrate Moon and planet orbits in solar system barycentric (SSB) frame. Also integrate dynamical partial derivatives for orbit & other parameters.

Frames, Clocks, Computation– 2 • Calculate time-of-flight: iterate up-leg (Earth station to Moon reflector) and down-leg (Moon to Earth) computation. • Calculated time-of-flight starts with transmit time, converts to TDB, retrieves Earth and Moon positions and velocities from integrated ephemeris.

Frames, Clocks, Computation– 3 • Lorentz contractions and scale changes (from potential) are applied to geocentric station locations and Moon centered reflector positions. • Relativistic (Shapiro) delay and atmospheric delay are added to the geometrical ranges.

Frames, Clocks, Computation– 4 • The calculated receive time – transmit time interval in TDB is converted to the station time interval. • Partial derivatives of range with respect to solution parameters are computed after the light-time iterations converge. • The least-squares solution fits the range model to observed range.

Sensitivities • Most of the sensitivity to gravitational physics parameters comes through the orbit dynamics, but PPN ϒ also depends on the gravitational (Shapiro) time delay. • We can solve for equivalence principle (Mg/Mi), PPN β & ϒ, geodetic precession, (d. G/dt)/G, & d(scale)/dt.

Data Weighting, Residuals • During the fits, the data are weighted. Weighting depends on combined instrumental error (from station) and model error (~0. 1 nsec = 1. 5 cm). • The quality of the fits can be monitored by examining postfit residuals by time, station, & retroreflector. • We can examine spectra of residuals.

Largest Radial Amplitudes by Cause –Ellipticity –Solar perturbations –Jupiter perturbation –Venus perturbations –Earth J 2 –Moon J 2 & C 22 –Earth C 22 –Solar radiation pressure Amplitude 20905 & 570 km 3699 & 2956 km 1. 06 km 0. 73, 0. 68 & 0. 60 km 0. 46 & 0. 45 km 0. 2 m 0. 5 mm 4 mm

Relativistic Effects on Orbit Cause – Lorentz contraction – Solar potential – Time transformation – Other relativity Amplitude 0. 95 m 6 cm 5 & 5 cm Sources: Chapront-Touzé and Chapront; Vokrouhlicky; Williams and Dickey

Causes of Perigee and Node Precessions Cause perigee rate "/yr node rate "/yr Sun 146, 425. 38 – 69, 671. 67 Planets 2. 47 – 1. 44 Earth J 2 6. 33 – 5. 93 Moon J 2 & C 22 – 0. 0176 – 0. 1705 Relativity 0. 0180 0. 0190

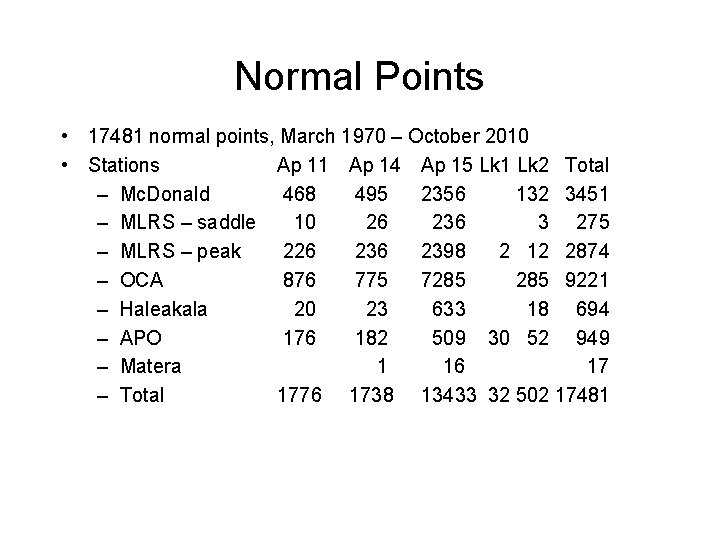
Normal Points • 17481 normal points, March 1970 – October 2010 • Stations Ap 11 Ap 14 Ap 15 Lk 1 Lk 2 Total – Mc. Donald 468 495 2356 132 3451 – MLRS – saddle 10 26 236 3 275 – MLRS – peak 226 2398 2 12 2874 – OCA 876 775 7285 9221 – Haleakala 20 23 633 18 694 – APO 176 182 509 30 52 949 – Matera 1 16 17 – Total 1776 1738 13433 32 502 17481

Equivalence Principle • The equivalence principle (EP) test is sensitive to the gravitational/inertial mass ratio difference between the Earth and Moon. Mg/Mi = (1. 4± 1. 2)x 10– 13 • Equivalent to a range amplitude of 4. 1± 3. 5 mm at 29. 53 days period.

Strong Equivalence Principle and PPN β • Convert the LLR EP result to strong EP by subtracting Adelberger’s (2001) weak EP result of (1. 0± 1. 4)x 10– 13. That gives (Mg/Mi)SEP = (0. 4± 1. 9)x 10– 13 η = 0. 00009± 0. 00042 • Using the Cassini result for ϒ leads to PPN β– 1 = (3± 11)x 10– 5

EP Warning • The preceding EP solution fixed the 4 annual nutation coefficients to IERS values. Also solving for the 4 imperfectly known nutation coefficients gives EP uncertainties ~2. 5 times larger! Those LLR-determined nutation uncertainties are 0. 2 -0. 5 mas. VLBI should give better values, but coefficients vary ~0. 1 mas due to geophysical effects. • Seasonal & diurnal geophysical effects affect station positions, geocenter motion, and nutations. These will corrupt the LLR EP test.

EP Warning Continued • A caution – projecting future LLR EP uncertainties by scaling in proportion to much smaller range errors is not valid. Geophysical effects will become limiting error sources at some level.

Geodetic Precession • The correction to the nominal geodetic or de Sitter-Fokker precession is modeled as a dimensionless factor Kgp = 0. 0035± 0. 0026 • That geodetic precession rate change is 0. 07± 0. 05 mas/yr compared to 19. 2 mas/yr. • The accuracy of the geodetic precession depends on time span and will improve for longer spans.

d. G/dt and Scale Change • The rate of change of the gravitational constant is = (8± 5)x 10– 13 /yr • Scale rate is geometrical, no dynamics d(scale)/dt = (-5± 5)x 10– 12 /yr • The solar system does not share the cosmic expansion of 1/13. 7 x 109 yr = 7. 3 x 10– 11 /yr by either comparison.

Future • Future LLR data is important. Both high accuracy ranges, such as Apache Point provides, and improved accuracy analysis software benefit all results. A longer data span benefits geodetic precession and change in G. • New retroreflectors could be placed on the Moon by future missions.

Conclusions • Lunar Laser Ranging continues to test gravitational physics. • A high accuracy model is necessary for LLR data analysis. • LLR results for equivalence principle, geodetic precession, d. G/dt and scale rate are consistent with general relativity

Looking Forward • Laser ranging to the Moon can continue to provide and improve gravitational physics results.