LL1 Parsing Programming Language Concepts Lecture 7 Prepared

LL(1) Parsing Programming Language Concepts Lecture 7 Prepared by Manuel E. Bermúdez, Ph. D. Associate Professor University of Florida

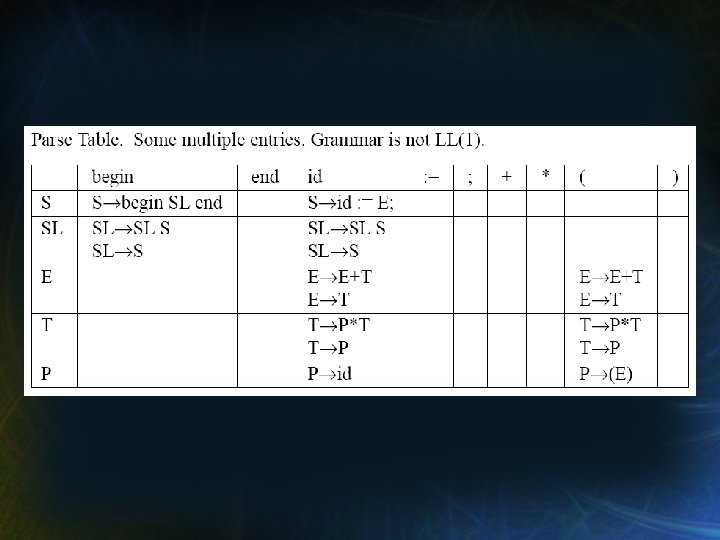
Example • Build the LL(1) parse table for the following grammar. → → SL → → E → → T → → P → → S begin SL end {begin} id : = E; {id} SL S {begin, id} * S {begin, id} E+T {(, id} * T {(, id} P*T {(, id} * P {(, id} (E) {(} * - not LL(1) id {id}

Example (cont’d) • Lemma: Left recursion always produces a non-LL(1) grammar (e. g. , SL, E above) • Proof: Consider A → First ( ) or Follow (A) First ( ) Follow (A)

Problems with our Grammar 1. SL is left recursive. 2. E is left recursive. 3. T → P * T both begin with the same → P sequence of symbols (P).

Solution to Problem 3 • Change: T → P * T → P { (, id } • to: { (, id } {*} { +, ; , ) } Follow(X) Follow(T) Follow(E) = { +, ; , ) } T→PX X→*T → due due and Disjoint! to T → P X to E → E+T , E → T to E → E+T, S → id : = E ; P → (E)

Solution to Problem 3 (cont’d) • In general, change A → 1 → 2. . . → n to A → X X → 1. . . → n Hopefully all the ’s begin with different symbols

Solution to Problems 1 and 2 • We want (…((( T + T)…) • Instead, (T) (+T) … (+T) Change: To: E→E+T → T E→ TY Y→ +TY → { (, id } {+} { ; , )} • Follow(Y) Follow(E) • ={; , )} No longer contains ‘+’, because we eliminated the production E → E + T

Solution to Problems 1 and 2 (cont’d) • In general, Change: to: A → A 1. . . → A n A→ 1. . . → m A → 1 X. . . → m X X → 1 X. . . → n X →

Solution to Problems 1 and 2 (cont’d) • In our example, Change: To: SL → SL S { begin, id } → S { begin, id } SL → S Z Z→SZ → { begin, id } { end }

Modified Grammar S SL Z E Y T X P → → → → begin SL end id : = E ; S Z T Y + T Y P X * T (E) id {begin} {id} {begin, id} {end} (, id} {+} {; , )} {(, id} {*} {; , +, )} {(} {id} Disjoint. Grammar is LL(1)

Recursive Descent Parsing • Top-down parsing strategy, suitable for LL(1) grammars. • One procedure per nonterminal. • Contents of stack embedded in recursive call sequence. • Each procedure “commits” to one production, based on the next input symbol, and the select sets. • Good technique for hand-written parsers.

For our Modified, LL(1) Grammar S; {S → begin SL end → id : = E; } “Read (T_X)” case Next_Token of verifies that T_begin : Read(T_begin); the upcoming SL; token is X, and Read (T_end); consumes it. T_id : Read(T_id); Read (T_: =); E; “Next_Token” Read (T_; ); is the upcoming otherwise Error; token. end; proc

For our Modified, LL(1) Grammar (cont’d) proc SL; {SL → SZ} S; Technically, should have insisted Z; that Next Token be either T_begin or T_id, but S will do end; that anyway. Checking early would aid error recovery. proc E; {E → TY} T; Y; // Ditto for T_( and T_id. end;

For our Modified, LL(1) Grammar (cont’d) proc Z; {Z → SZ → } case Next Token of T_begin, T_id: S; Z; T_end: ; otherwise Error; end;

For our Modified, LL(1) Grammar (cont’d) proc Y; {Y → +TY Could have used a → } case statement if Next Token = T_+ then Read (T_+) T; Y; end; proc T; {T → PX} P; Could have checked for T_( and T_id. X end;

For our Modified, LL(1) Grammar (cont’d) proc X; {X → *T → } if Next Token = T_* then Read (T_*); T; end;

For our Modified, LL(1) Grammar (cont’d) →(E) → id } case Next Token of T_(: Read (T_(); E; Read (T_)); T_id: Read (T_id); otherwise Error; end; proc P; {P

LL(1) Parsing Programming Language Concepts Lecture 7 Prepared by Manuel E. Bermúdez, Ph. D. Associate Professor University of Florida