Linking Probability to Statistical Inference Concepts in Statistics

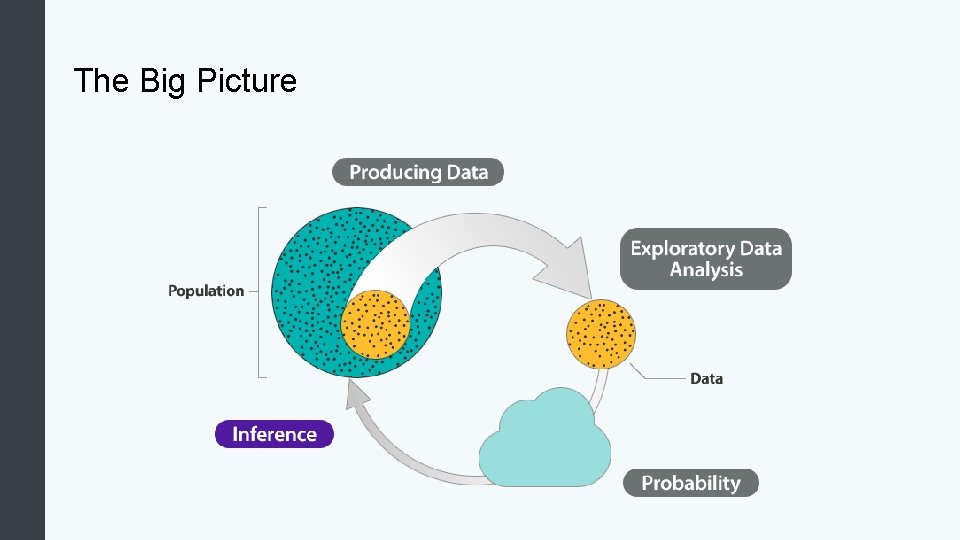
The Big Picture

Probability Statistical inference always involves an argument based on probability. Recall the following important points about probability • Probability is a measure of how likely an event is to occur. • We can make probability statements only about random events. Random here means that the outcome is uncertain in the short run but has a predictable pattern in the long run.

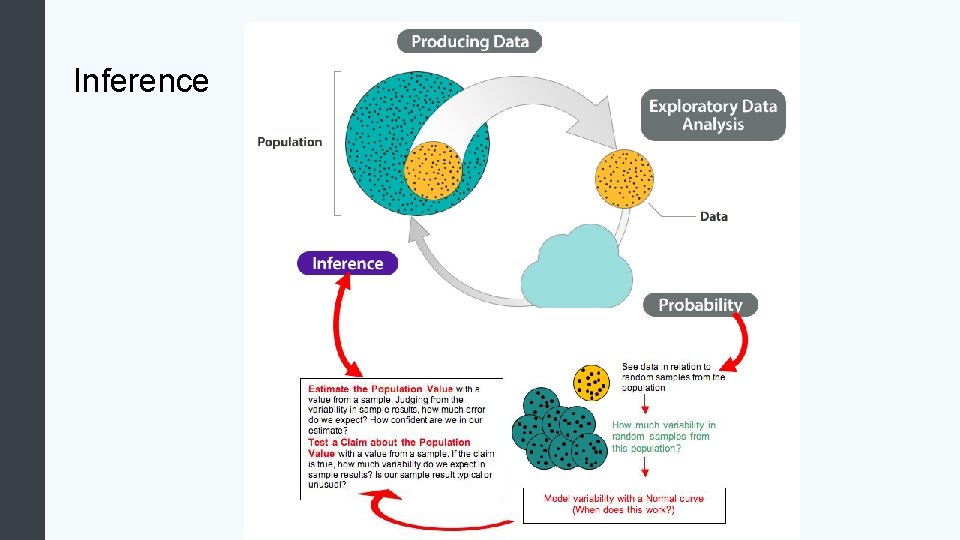
Inference

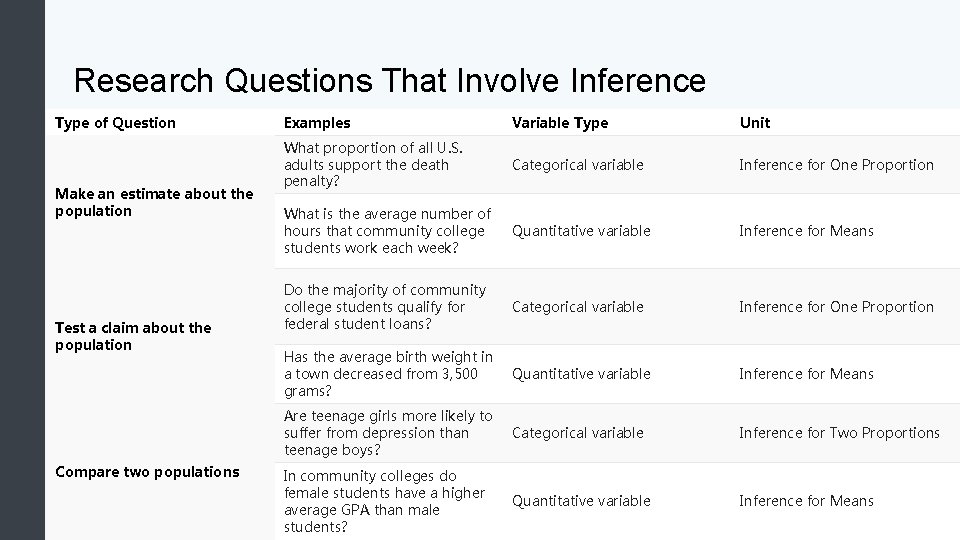
Research Questions That Involve Inference Type of Question Make an estimate about the population Test a claim about the population Compare two populations Examples Variable Type Unit What proportion of all U. S. adults support the death penalty? Categorical variable Inference for One Proportion What is the average number of hours that community college students work each week? Quantitative variable Inference for Means Do the majority of community college students qualify for federal student loans? Categorical variable Inference for One Proportion Has the average birth weight in a town decreased from 3, 500 grams? Quantitative variable Inference for Means Are teenage girls more likely to suffer from depression than teenage boys? Categorical variable Inference for Two Proportions In community colleges do female students have a higher average GPA than male students? Quantitative variable Inference for Means

Inference Each research question from the previous slide relates to either a categorical variable or a quantitative variable. In this course, three criteria determine the inference procedure we use: • • • The type of variable. The type of inference (estimate a population value or test a claim about a population value). The number of populations involved.

Proportions from Random Samples Vary Imagine a small college with only 200 students, and suppose that 60% of these students are eligible for financial aid. • Population: 200 students at the college • Variable: Eligibility for financial aid is a categorical variable, so we use a proportion as a summary • Population proportion: 0. 60 of the population is eligible for financial aid

Parameters vs. Statistics One of the goals of inference is to draw a conclusion about a population on the basis of a random sample from the population. • • A parameter is a number that describes a population. A statistic is a number that we calculate from a sample. When we do inference, the parameter is not known because it is impossible or impractical to gather data from everyone in the population. • We make an inference about the population parameter on the basis of a sample statistic. • Statistics from samples vary. If the variable is categorical, the parameter and the statistic are both proportions. If the variable is quantitative, the parameter and statistic are both means.

Parameters vs. Statistics Different notation for parameters and statistics: (Population) Parameter (Sample) Statistic Proportion Mean Standard Deviation Sometimes we refer to the sample statistics as “p-hat” and “x-bar. ”

Random Sampling •

The Sampling Distribution of Sample Proportions •

Applying the Model for Sampling Distribution Compare the mean and standard deviation observed in the simulation to the model. The conditions are met, so a normal model is a good fit. The model is a good description of the center, spread, and shape we observed in the simulation.

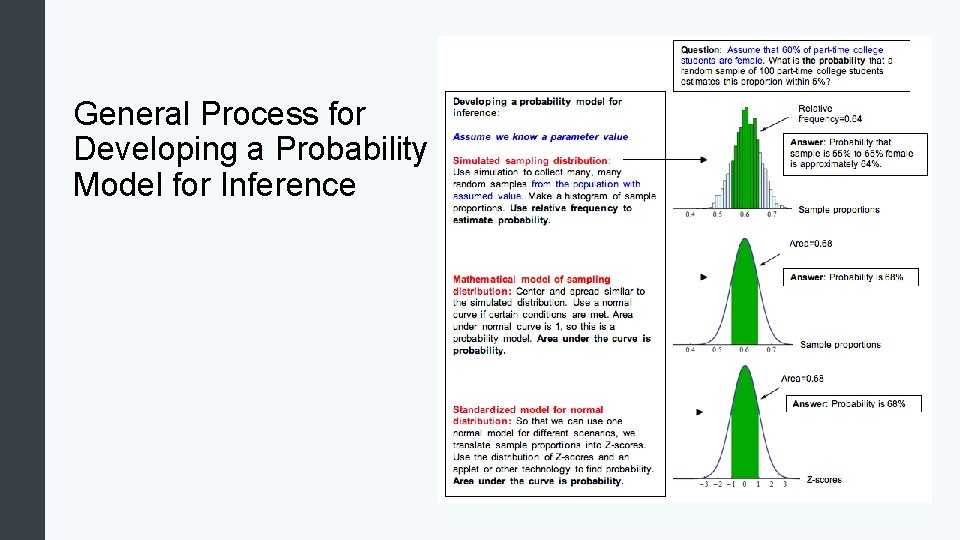
General Process for Developing a Probability Model for Inference

Sampling Distribution •

Statistical Inference Our goal in statistical inference is to infer from the sample data some conclusion about the wider population the sample represents. Statistical inference uses the language of probability to say how trustworthy our conclusions are. Two types of inference: confidence intervals and hypothesis tests We construct a confidence interval when our goal is to estimate a population parameter. We conduct a hypothesis test when our goal is to test a claim about a population parameter.

Confidence Interval •

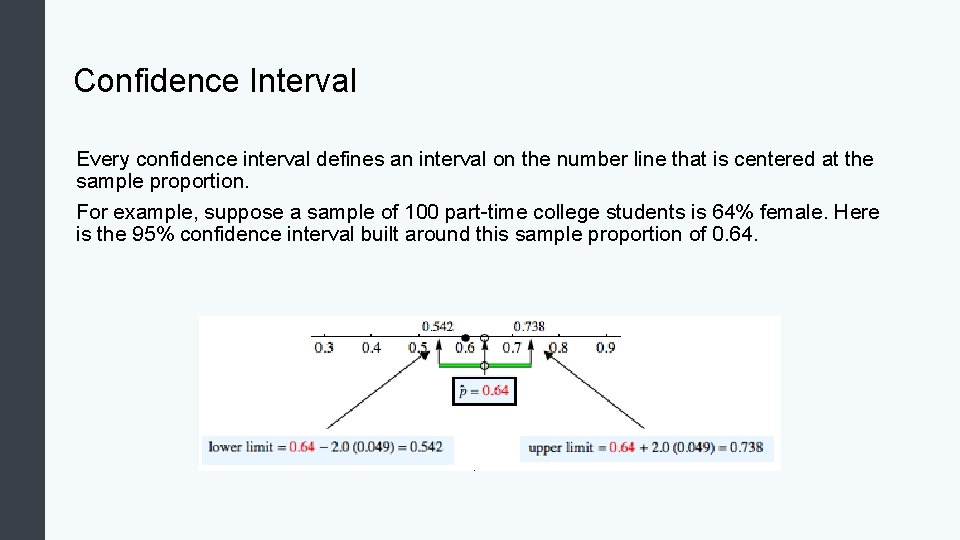
Confidence Interval Every confidence interval defines an interval on the number line that is centered at the sample proportion. For example, suppose a sample of 100 part-time college students is 64% female. Here is the 95% confidence interval built around this sample proportion of 0. 64.

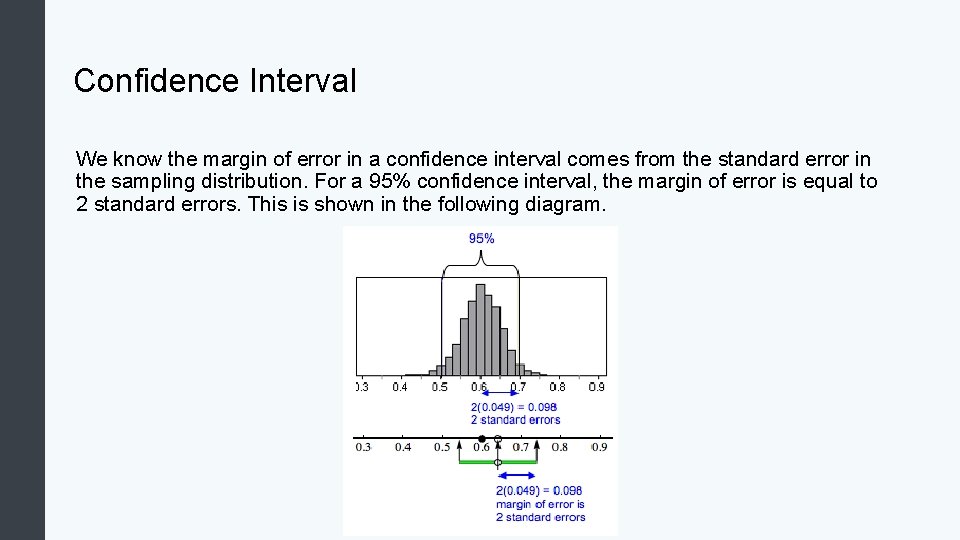
Confidence Interval We know the margin of error in a confidence interval comes from the standard error in the sampling distribution. For a 95% confidence interval, the margin of error is equal to 2 standard errors. This is shown in the following diagram.

Hypothesis Tests The purpose of a hypothesis test is to use sample data to test a claim about a population parameter. We make a claim about a population proportion. From the claim, we state an assumption about the value of the population proportion. We construct a simulation or a normal model to represent the sampling distribution that occurs when sampling from a population with this assumed value. If the normal model is a good fit for the sampling distribution, we can find a z-score and use a simulation to associate a probability with a “likely” or “unlikely” statement.

Hypothesis Tests: Example •

Hypothesis Tests: Example continued •

Quick Review • • • What is inference based on? What are two types of inference procedures? What is a parameter? Larger samples have more or less variability? What is the purpose of a confidence interval? When a normal model is a good fit for the sampling distribution, the 95% confidence interval has a margin of error equal to ?